If equivalent resistances of R1andR2 in series and parallel be r1andr2 respectively, then R1R2 equals
r1r2
r1r2r1+r2
r+√r21−4r1r2r1+√r21+4r1r2
r+√r21−4r1r2r1−√r21+4r1r2
The correct Answer is:D
To solve the problem, we need to find the ratio of the equivalent resistances R1R2 when resistors R1 and R2 are connected in series and parallel.
1. Understand the Equivalent Resistance in Series:
- When two resistors R1 and R2 are connected in series, the equivalent resistance r1 is given by:
r1=R1+R2
2. Understand the Equivalent Resistance in Parallel:
- When the same resistors are connected in parallel, the equivalent resistance r2 is given by:
1r2=1R1+1R2
- This can be rearranged to:
r2=R1R2R1+R2
3. Set Up the Ratio:
- We need to find the ratio R1R2. To do this, we will express both r1 and r2 in terms of R1 and R2.
4. Express r1 and r2:
- From step 1, we have:
r1=R1+R2
- From step 2, we have:
r2=R1R2R1+R2
5. Relate r1 and r2:
- We can express R1 in terms of r1 and r2:
R1=r1−R2
- Substitute R2 from the equation of r2:
R2=r2(R1+R2)R1
6. Solve for R1R2:
- From the equations derived, we can manipulate them to find the ratio R1R2:
R1R2=(r1−R2)R2
- By substituting R2 from the equation of r2 and simplifying, we can derive the final ratio.
7. Final Result:
- After simplification, we find:
R1R2=2
Conclusion:
The ratio R1R2 equals 2.
- When two resistors R1 and R2 are connected in series, the equivalent resistance r1 is given by:
r1=R1+R2
- When the same resistors are connected in parallel, the equivalent resistance r2 is given by:
1r2=1R1+1R2
- This can be rearranged to:
r2=R1R2R1+R2
- We need to find the ratio R1R2. To do this, we will express both r1 and r2 in terms of R1 and R2.
- From step 1, we have:
r1=R1+R2
- From step 2, we have:
r2=R1R2R1+R2
- We can express R1 in terms of r1 and r2:
R1=r1−R2
- Substitute R2 from the equation of r2:
R2=r2(R1+R2)R1
- From the equations derived, we can manipulate them to find the ratio R1R2:
R1R2=(r1−R2)R2
- By substituting R2 from the equation of r2 and simplifying, we can derive the final ratio.
- After simplification, we find:
R1R2=2
The ratio R1R2 equals 2.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Two spherical nuclei have mass number 216 and 64 with their radii R1andR2 respectively. The ratio, R1R2 is equal to
A3:2B1:3C1:2D2:3Consider two resistors R1 and R2 in series. The current flowing through R1 and R2 is
AR1=/,R2=2/BR1=/2,R2=1/2CR1=/,R2=/DR1=1/2,R2=2/Two resistances R1andR2 provides series to parallel equivalents as n/1, then the correct relationship is
A(R1R2)3/2+(R2R1)3/2=n3/2B(R1R2)3+(R2R1)3=n3C(R1R2)2+(R2R1)2=n2D(R1R2)1/2+(R2R1)1/2=n1/2
Two resistors of resistances R1=100±3 ohm and R2=200±4 ohm are connected (a) in series, (b) in parallel. Find the equivalent resistance of the (a) series combination, (b) parallel combination. Use for (a) the relation R=R1+R2 and for (b) 1R'=1R1+1R2 and ΔR'R'2=ΔR1R21+ΔR2R22
View SolutionFour identical resistance are joined as shown in fig. the equivalent resistance between points A and B is R1 and that between A and C is R2. Then ratio of R1R2 is
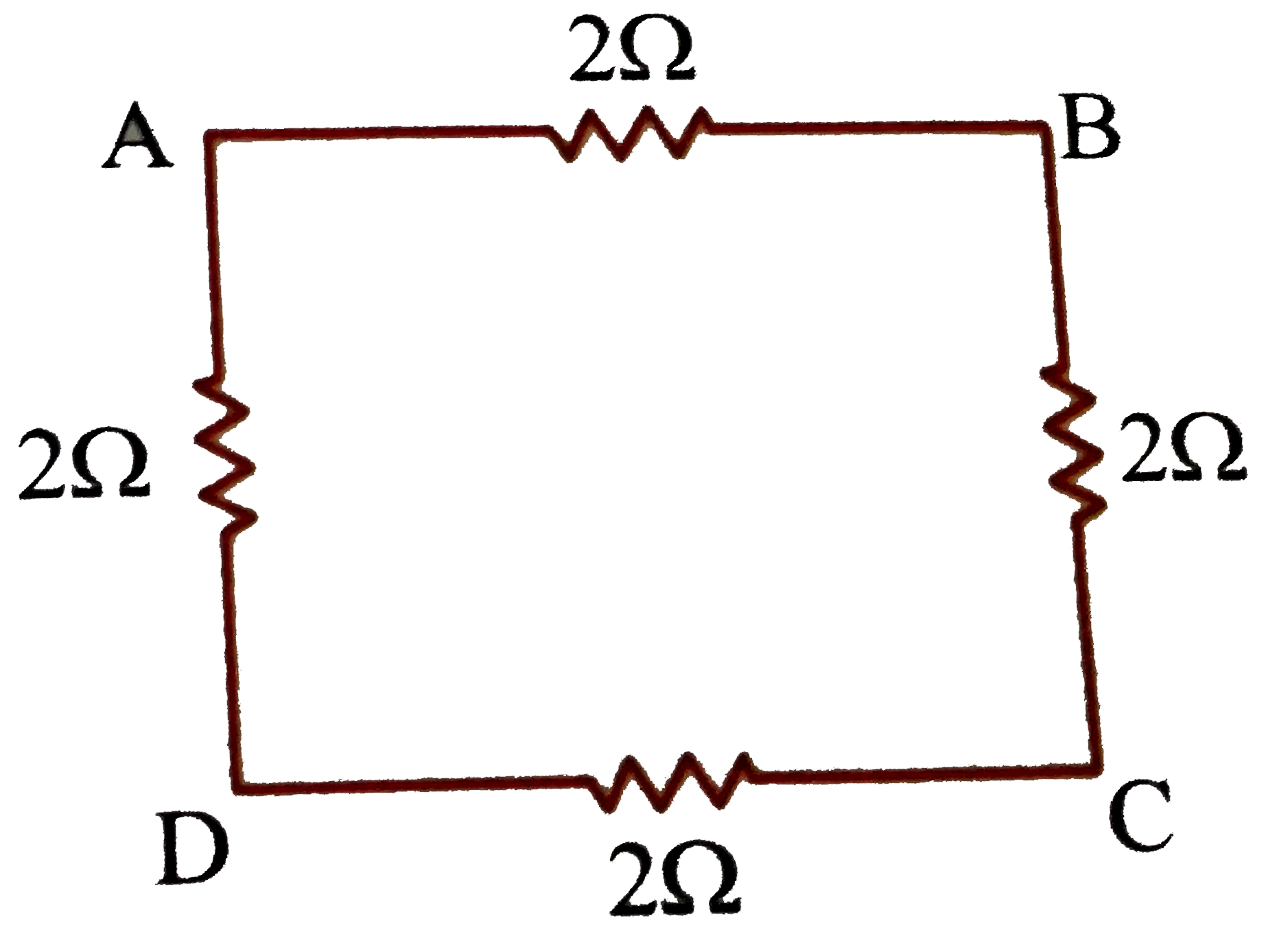
View SolutionSix resistance each of value r=5Ω are connected between points A, B and C as shown in figure. If R1,R2 and R3 are the net resistance between A and B, between B and C and between A and C respectively, then R1:R2:R3 will be equal to

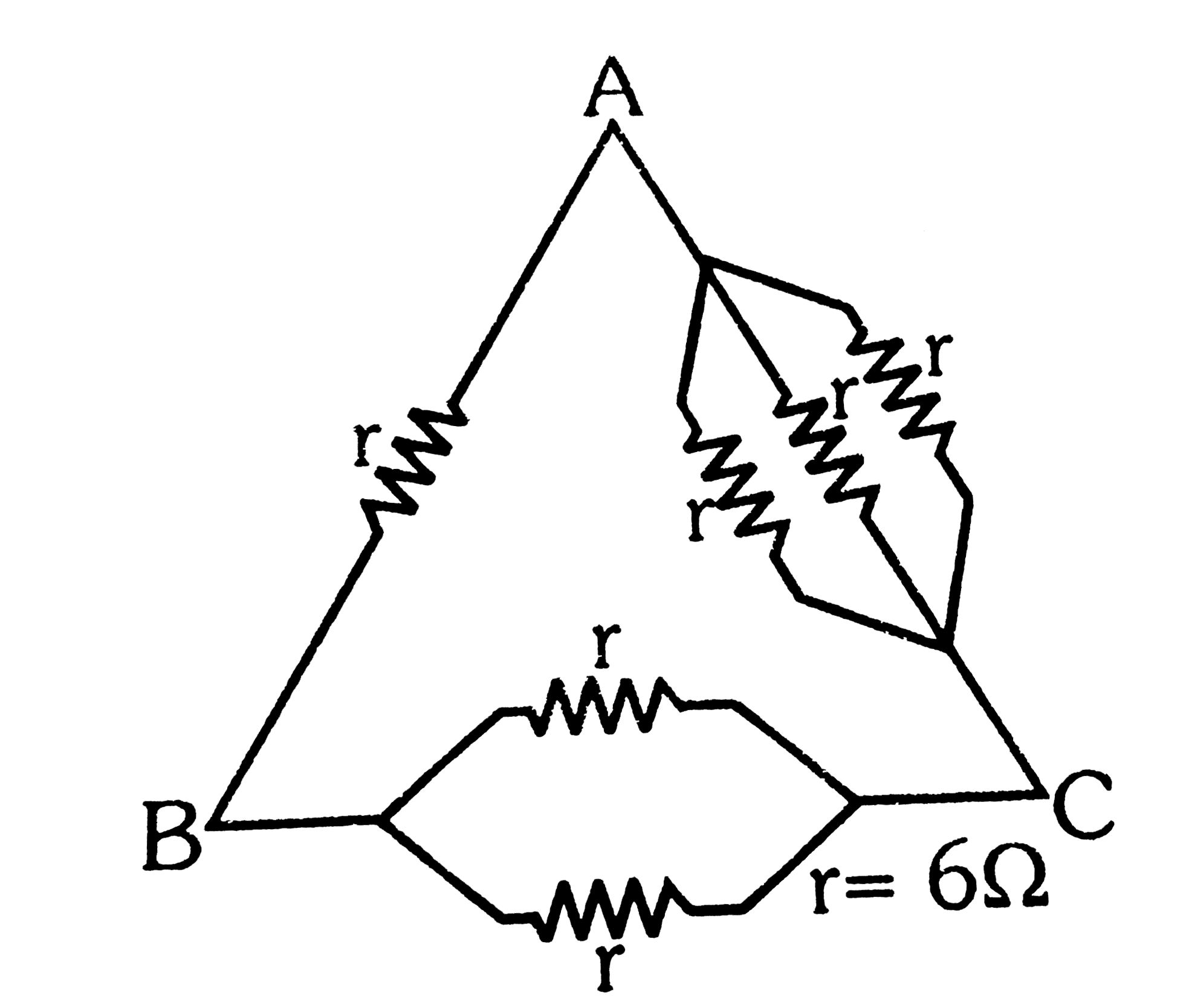
View SolutionSix resistances each of v ale r=6Ω are connected between points A,B and C as shown in the figure if R1,R2 and R3 are the net resistances between A and B, between B and C and between A and C respectively, the R1:R2:R3 will be equal to
View SolutionTwo resistance R1 and R2 when connected in series and parallel with 120V line, power consumed will be 25W and 100W respectively. . Then the ratio of power consumed by R1 to that consmed by R2 will be
View Solution
