If radius if earth is reduced to half without changing its mass, then match the following columns
Column-IColumn-II(A)Angular momentum of earth(p)Will become two times(B)Time period of rotation of earth(q)Will become four times(C)Rotational kinetic energy of earth(r)Will remain constant(D)(s)None
The correct Answer is:(A→q,B→s,c→q)
To solve the problem, we need to analyze how the angular momentum, time period of rotation, and rotational kinetic energy of the Earth change when its radius is reduced to half while keeping its mass constant.
1. Angular Momentum of Earth (L):
- The angular momentum L is given by the formula:
L=I⋅ω
where I is the moment of inertia and ω is the angular velocity.
- The moment of inertia I for a solid sphere is:
I=25mr2
- If the radius is reduced to half, the new radius r2=r2:
I2=25m(r2)2=25m⋅r24=110mr2
- By conservation of angular momentum:
L1=L2⟹I1⋅ω1=I2⋅ω2
- Substituting the values:
25mr2⋅ω=110mr2⋅ω2
- Canceling mr2 from both sides:
25⋅ω=110⋅ω2⟹ω2=4⋅ω
- Since angular momentum is conserved, it remains constant:
L will remain constant.
- Thus, (A) matches with (r).
2. Time Period of Rotation (T):
- The time period T is related to angular velocity by:
T=2πω
- The new angular velocity ω2=4⋅ω:
T2=2πω2=2π4ω=14T1
- This indicates that the time period of rotation will decrease:
T will become 14 of the original time period.
- Thus, (B) matches with (s) (none of the options).
3. Rotational Kinetic Energy (K):
- The rotational kinetic energy is given by:
K=12Iω2
- Initial kinetic energy:
K1=12⋅25mr2⋅ω2=15mr2⋅ω2
- Final kinetic energy:
K2=12⋅110mr2⋅(4ω)2=12⋅110mr2⋅16ω2=810mr2⋅ω2=45mr2⋅ω2
- Thus, the final kinetic energy is:
K2=4⋅K1
- Therefore, (C) matches with (q).
Final Matching:
- (A) Angular momentum of earth → (r) Will remain constant
- (B) Time period of rotation of earth → (s) None
- (C) Rotational kinetic energy of earth → (q) Will become four times
- The angular momentum L is given by the formula:
L=I⋅ω
where I is the moment of inertia and ω is the angular velocity.
- The moment of inertia I for a solid sphere is:
I=25mr2
- If the radius is reduced to half, the new radius r2=r2:
I2=25m(r2)2=25m⋅r24=110mr2
- By conservation of angular momentum:
L1=L2⟹I1⋅ω1=I2⋅ω2
- Substituting the values:
25mr2⋅ω=110mr2⋅ω2
- Canceling mr2 from both sides:
25⋅ω=110⋅ω2⟹ω2=4⋅ω
- Since angular momentum is conserved, it remains constant:
L will remain constant.
- Thus, (A) matches with (r).
- The time period T is related to angular velocity by:
T=2πω
- The new angular velocity ω2=4⋅ω:
T2=2πω2=2π4ω=14T1
- This indicates that the time period of rotation will decrease:
T will become 14 of the original time period.
- Thus, (B) matches with (s) (none of the options).
- The rotational kinetic energy is given by:
K=12Iω2
- Initial kinetic energy:
K1=12⋅25mr2⋅ω2=15mr2⋅ω2
- Final kinetic energy:
K2=12⋅110mr2⋅(4ω)2=12⋅110mr2⋅16ω2=810mr2⋅ω2=45mr2⋅ω2
- Thus, the final kinetic energy is:
K2=4⋅K1
- Therefore, (C) matches with (q).
- (A) Angular momentum of earth → (r) Will remain constant
- (B) Time period of rotation of earth → (s) None
- (C) Rotational kinetic energy of earth → (q) Will become four times
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (A) Chapter Exercises
83 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
If earth decreases its rotational speed. Match the following columns
Column-IColumn-II(A)Value of g at pole(p)Will remain same(B)Value of g at equator(q)Will increase(C)Distance of geostationary(r)Will decrease(D)Energy of geostationary satellite(s)Cannot say
View SolutionMatch the following columns
Column-IColumn-II(A)Time period of an earthsatellite in circular orbit(p)Independent of mass of satellite(B)Orbital velocity of satellite(q)Independent of radius of orbit(C)Mechanical energy of satellite(r)Independent of mass of earth(s)None
View SolutionA solid sphere is rotating about an axis shown in figure. An insect follows the dotted path on the circumference of sphere as shown in the figure.
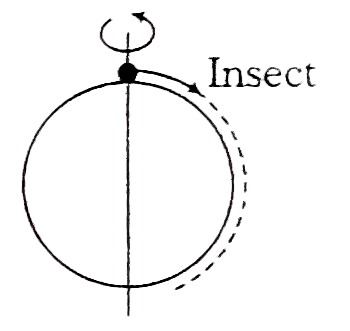
Column-IColumn-II(A)Moment of inertia(p)Will remain constant(B)Angular velocity(q)Will first increase, then decrease(C)Angular momentum(r)Will first decrease then increase(D)Rotational kinetic energy(s)Will continuously decrease(t)Will continuously increase
View SolutionIf earth radius reduces to half of its present value then the time period of rotation will become:
View SolutionDensity of a planet is two times the density of earth. Radius of this planet is half. Match the following (as compared to earth)
Column-IColumn-II(A)Accleration due to gravity on this planet's surface(p)Half(B)Gravitational potential on the surface(q)Same(C)Gravitational potential at centre(r)Two times(D)Gravitational field strength at centre(s)Four times
View SolutionMatch the following :
Column -IColumn -II(A)Acceleration due to gravity(p)Kepler's law(B)Law of periods(q)Vector quantity(C)Orbital speed(r)Uniform near earth surface(D)Gravitational potential(s)Is nearly zero at infinity
View SolutionIn Bohr's atomic model for hydrogen like atoms match the following column :
Column IColumn II(A)If electron jumps from n = 32 to n = 1(p)Speed of electron will become 2 times(B)If electron jumps from n = 1 to n = 4(q)Kinetic energy of electron will become 4 time(C)If electron jumps from n = 4 to n = 4(r)Angular momentum of electron will becomes 2 times(s)Angular velocity of electron will becomes 4 times(t)None.
View SolutionA particle of mass m, kinetic energy K and momentum p collides head on elastically with another particle of mass 2m at rest. After collision, :
Column IColumn II(A)Momentum of first particle(p)3/4p(B)Momentum of second particle(q)−K/9(C)Kinetic energy of first particle(r)−p/3(D)Kinetic energy of second particle(s)8K9(t)None
View SolutionMatch the following columns.
Column IColumn II(A)Longitudinal stress(p)Volume changes(B)Shear stress(q)Shape change(C)Volumetric stress(r)Volume does not changes(D)Tensile stress(s)Shapes does not change
View SolutionMatch the following columns. (for a satellite in circular orbit)
Column-IColumn-II(A)Kinetic energy(p)−GMm2r(B)Potential energy(q)√GMr(C)Total energy(r)−GMmr(D)Orbital speed(s)GMm2r
View Solution
