If the container filled with liquid gets accelerated horizontally or vertically, pressure in liquid gets changed. In liquid (ay) for calculation of pressure, effective g is used. A closed box horizontal base 6m by 6m and a height 2m is half filled with liquid. It is given a constant horizontal acceleration g/2 and vertical downward acceleration g/2.
Water pressure at the bottomof centre of the box is equal to (atmospheric pressure =105N/m2 density of water =1000kg/m3,g=10m/s2)
1.1MPa
0.11MPa
0.101MPa
0.011MPa
The correct Answer is:B
P=Pa+ρgh=105−1000x10×1
=(105+104)N/m2=0.11MPa
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - True/False
1 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - SCQ_TYPE
13 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Assertion-Reasoning
8 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
For the motion of a projectile in a vertical plane, horizontal acceleration is ____ and vertical downward acceleration is equal to .
View SolutionA liquid kept in a container has a horizontal acceleration 'a' as shown in figure.
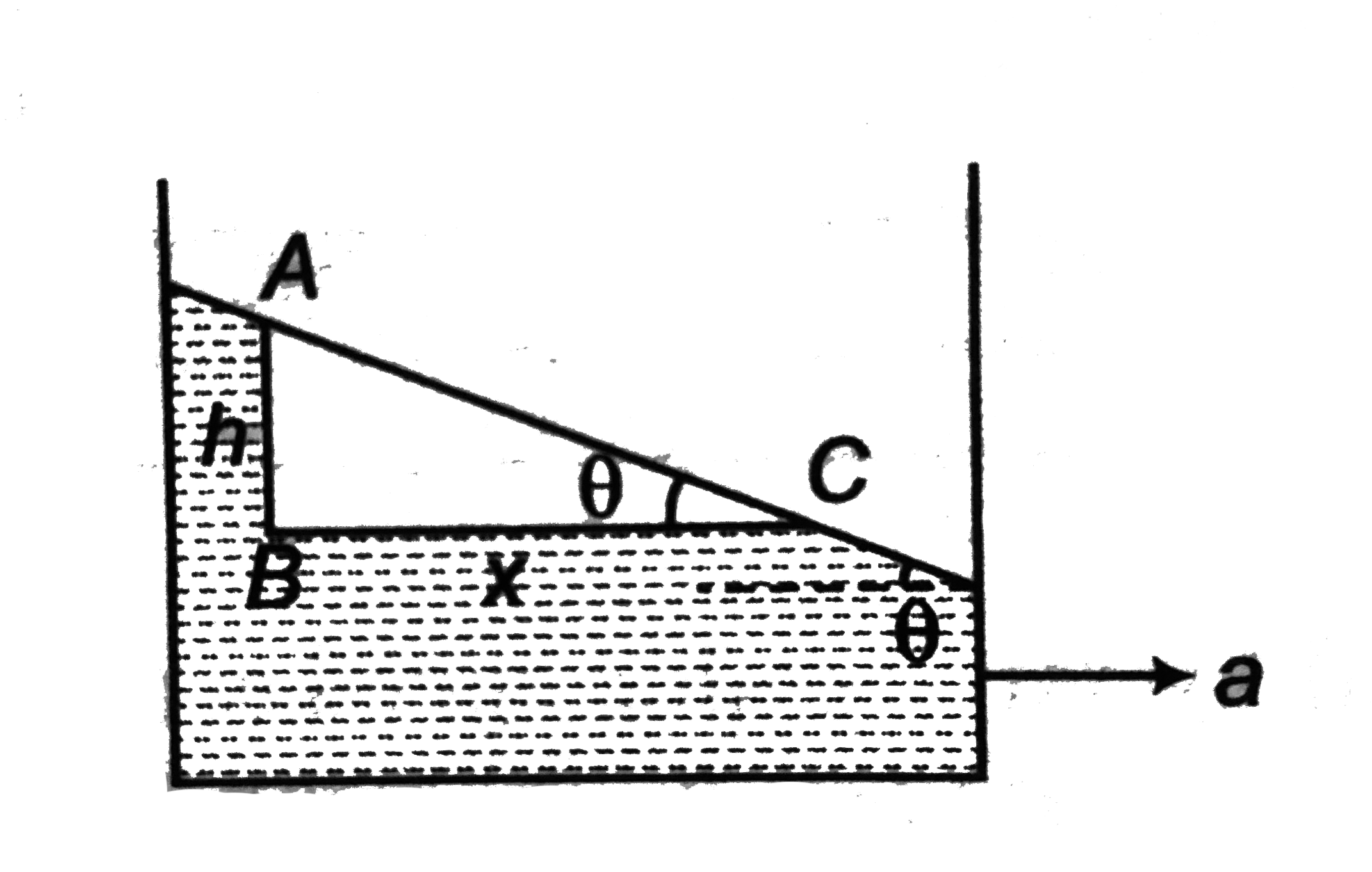
Using the pressure equation along the path ABC find the angle θ.
View Solution
Knowledge Check
If the container filled with liquid gets accelerated horizontally or vertically, pressure in liquid gets changed. In liquid (ay) for calculation of pressure, effective g is used. A closed box horizontal base 6m by 6m and a height 2m is half filled with liquid. It is given a constant horizontal acceleration g/2 and vertical downward acceleration g/2.
The maximum value of water pressure in the box is equal toA1.4MPaB0.14MPaC0.104MPaD0.014MPaIf the container filled with liquid gets accelerated horizontally or vertically, pressure in liquid gets changed. In liquid (ay) for calculation of pressure, effective g is used. A closed box horizontal base 6m by 6m and a height 2m is half filled with liquid. It is given a constant horizontal acceleration g/2 and vertical downward acceleration g/2.
Length of exposed portion of top of box is equal toA2mB3mC4mD2.5mIf the container filled with liquid gets accelerated horizontally or vertically, pressure in liquid gets changed. In liquid (ay) for calculation of pressure, effective g is used. A closed box horizontal base 6m by 6m and a height 2m is half filled with liquid. It is given a constant horizontal acceleration g/2 and vertical downward acceleration g/2.
The angle of the free surface with the horizons is equal toA30∘Btan−123Ctan−1 13D45∘
Figure shows an L-shaped tube tilled with a liquid to a height H. What should be the horizontal acceleration a of the tube so that the pressure at the point A becomes atmospheric.

View SolutionA cylinder of 4 m height is half filled with oil of density 0.72 g cm−3. If the Becond half of cylinder is filled with water, then find the pressure at the bottom of cylinder due to these liquids.
View SolutionIf the container filled with liquid gets accelerated horizontally or vertically, pressure in liquid gets changed. In liquid (ay) for calculation of pressure, effective g is used. A closed box horizontal base 6m by 6m and a height 2m is half filled with liquid. It is given a constant horizontal acceleration g/2 and vertical downward acceleration g/2.
What is the value of vertical acceleration of box for given horizontal acceleration (g/2), so that no part of the bottom of the box is exposed?
View SolutionIf a vessel containing a fluid of density ρ upto height h is accelerated vertically downwards with accelerations a0. Then the pressure by fluid at the bottom of a vessel is
View SolutionVapor pressure of a liquid changes with …… of the liquid.
View Solution
