If the Kα radiation of Mo(Z=42) has a wevelength of 0.71Å, calculate wevelength of the corresponding radiation of Cu,i.e.,kαforCu(Z=29) assuming b = 1.
To solve the problem, we need to find the wavelength of the K_alpha radiation for Copper (Cu, Z = 29) given the wavelength of K_alpha radiation for Molybdenum (Mo, Z = 42) and using the formula that relates the wavelengths with atomic numbers.
1. Identify Given Values:
- Wavelength of K_alpha radiation for Mo (Z = 42):
λ1=0.71Å
- Atomic number of Mo:
Z1=42
- Atomic number of Cu:
Z2=29
- Given b=1.
2. Use the Wavelength Ratio Formula:
The relationship between the wavelengths and atomic numbers is given by:
λ2λ1=(Z1−b)2(Z2−b)2
Substituting the known values:
λ20.71=(42−1)2(29−1)2
3. Calculate the Atomic Number Adjustments:
- For Mo:
Z1−b=42−1=41
- For Cu:
Z2−b=29−1=28
4. Substitute into the Ratio:
Now substituting these values into the equation:
λ20.71=412282
5. Calculate the Squares:
- 412=1681
- 282=784
6. Calculate the Ratio:
λ20.71=1681784
7. Cross Multiply to Solve for λ2:
λ2=0.71×1681784
8. Calculate λ2:
λ2=0.71×2.141=1.52Å(approximately)
Final Answer:
λ2≈1.52Å
- Wavelength of K_alpha radiation for Mo (Z = 42):
λ1=0.71Å
- Atomic number of Mo:
Z1=42
- Atomic number of Cu:
Z2=29
- Given b=1.
The relationship between the wavelengths and atomic numbers is given by:
λ2λ1=(Z1−b)2(Z2−b)2
Substituting the known values:
λ20.71=(42−1)2(29−1)2
- For Mo:
Z1−b=42−1=41
- For Cu:
Z2−b=29−1=28
Now substituting these values into the equation:
λ20.71=412282
- 412=1681
- 282=784
λ20.71=1681784
λ2=0.71×1681784
λ2=0.71×2.141=1.52Å(approximately)
λ2≈1.52Å
Topper's Solved these Questions
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Solved Examples
23 Videos
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Exercise 4.1
15 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Single Correct
10 Videos
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer
5 Videos
Similar Questions
The Kα line obtained for molybdenum (Z=42) is 0.71 Å. Then, the wavelength of the Kα line of copper (Z = 29) is
View SolutionThe Kα line from molybdenum (atomic number=42) has a wavelength off .7078Å. The wavelength off Kα line of zinc (atomic number=30) will be
View SolutionCalculate the wavelength of Kα line for the target made of tungsten (Z=74).
View SolutionIn Uranium (Z=92), the K absorption edge is 0.107 Å and the Kα line is 0.126 Å. The wavelength of the L absorption edge is
View SolutionStatement-1 : The frequency of Kα X-radiation is greater than Kβ for a given target material.
and
Statement-2 : Kα radiation is produced when an electron from n=2 jumps into the vacancy in n=1 orbit, whereas in Kβ radiation the transition takes place from n=2 to n=1.
View SolutionThe graph given below, shows the variation of √f vs z for characteristics X- rays. Lines 1,2,3 and 4 shown in the graph corresponds to any one of Kα,Kβ,Lα,Lβ emission, then Lβ is represented by ( f = frequency, z = Atomic number)
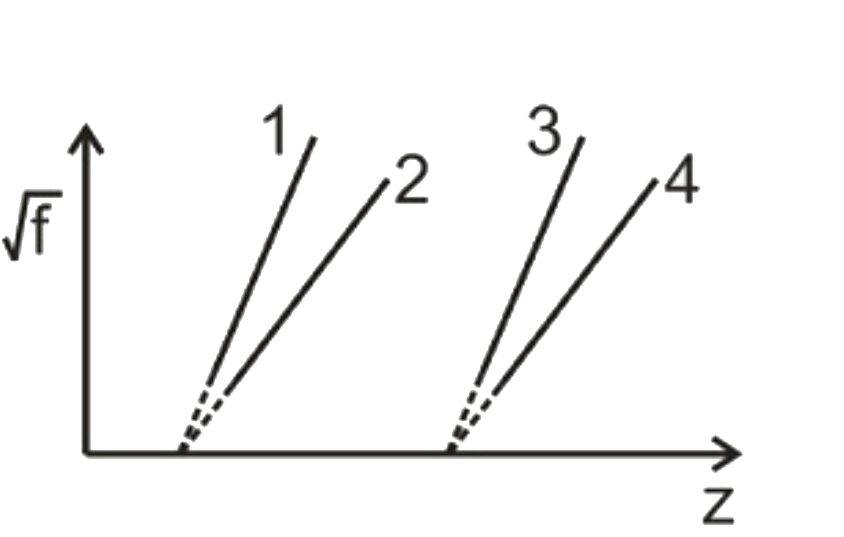
View SolutionX-ray emitted from a copper target and a molybdenum target are found to contains a line of wavelength 22.85nm attributed to the Kα line of an impurity element . The Kα line of copper (Z=29) and molybdenum (Z=42) have wavelength 15.42nmand7.12nm, respectively. The atomic number of the impurity element is
View SolutionFind the wavelength of the Kα line in copper (Z=29), if the wave length of the Kα line in iron (Z=26) is known to be equal to 193pm (Take b=1)
View SolutionThe wavelength of Kα X-ray line for an element is 0.42Å . Find the wavelength of Kβ line emitted by the same element.
View SolutionIf the wavelength of Kα radiation emitted an atom of atomic number Z = 41 is λ , then the atomic number for an atom that emits Kα radiation with the wavelength 4λ, is
View Solution
