If the maximum speed of a particle on a travelling wave is v0, then find the speed of a particle when the displacement is half of the maximum value.
v02
√3v04
√3v02
`v_(0)`
The correct Answer is:c
To solve the problem, we need to find the speed of a particle on a traveling wave when its displacement is half of the maximum value. Let's break down the solution step by step.
1. Understand the Wave Equation:
The standard equation for a traveling wave can be expressed as:
y=Asin(ωt−kx)
where A is the amplitude, ω is the angular frequency, t is time, k is the wave number, and x is the position.
Hint: Familiarize yourself with the wave equation and its parameters.
2. Find the Maximum Speed:
The speed of a particle on the wave can be found by differentiating the wave equation with respect to time t:
v=dydt=Aωcos(ωt−kx)
The maximum speed v0 occurs when cos(ωt−kx)=1:
v0=Aω
Hint: Remember that the maximum speed occurs when the cosine function equals 1.
3. Determine Displacement Condition:
We need to find the speed when the displacement y is half of the maximum value. Thus, we set:
y=A2
This implies:
A2=Asin(ωt−kx)
Dividing both sides by A (assuming A≠0):
12=sin(ωt−kx)
Hint: Use the sine function to relate displacement to the angle.
4. Find the Angle:
The equation sin(ωt−kx)=12 corresponds to angles where:
ωt−kx=30∘orωt−kx=150∘
For simplicity, we can use 30∘.
Hint: Recall the angles that yield a sine value of 12.
5. Calculate the Speed at Half Displacement:
Now, substitute ωt−kx=30∘ back into the velocity equation:
v=Aωcos(ωt−kx)=Aωcos(30∘)
Since Aω=v0:
v=v0cos(30∘)
The value of cos(30∘) is √32:
v=v0⋅√32
Hint: Use the known value of cosine for 30∘ to find the speed.
6. Final Result:
Thus, the speed of the particle when the displacement is half of the maximum value is:
v=√32v0
Conclusion:
The speed of a particle on a traveling wave when its displacement is half of the maximum value is √32v0.
The standard equation for a traveling wave can be expressed as:
y=Asin(ωt−kx)
where A is the amplitude, ω is the angular frequency, t is time, k is the wave number, and x is the position.
The speed of a particle on the wave can be found by differentiating the wave equation with respect to time t:
v=dydt=Aωcos(ωt−kx)
The maximum speed v0 occurs when cos(ωt−kx)=1:
v0=Aω
We need to find the speed when the displacement y is half of the maximum value. Thus, we set:
y=A2
This implies:
A2=Asin(ωt−kx)
Dividing both sides by A (assuming A≠0):
12=sin(ωt−kx)
The equation sin(ωt−kx)=12 corresponds to angles where:
ωt−kx=30∘orωt−kx=150∘
For simplicity, we can use 30∘.
Now, substitute ωt−kx=30∘ back into the velocity equation:
v=Aωcos(ωt−kx)=Aωcos(30∘)
Since Aω=v0:
v=v0cos(30∘)
The value of cos(30∘) is √32:
v=v0⋅√32
Thus, the speed of the particle when the displacement is half of the maximum value is:
v=√32v0
The speed of a particle on a traveling wave when its displacement is half of the maximum value is √32v0.
Topper's Solved these Questions
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Single Correct Answer
1 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Multiple Correct
25 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Subjective
16 Videos
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct
9 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
Maximum speed of a particle in simple harmonic motion is vmax. Then average speed of this particle in one time period is equal to
View SolutionA particle of mass 2 kg executing SHM has amplitude 10 cm and time period is 1 s.Find (i) the angular frequency (ii) the maximum speed (ii) the maximum acceleration (iv) the maximum restoring force (v) the speed when the displacement from the mean position is 8 cm (vi) the speed after 112 s the particle was at the extreme position (vii) the time taken by the particle to go directly from its mean position to half the amplitude (viii) the time taken by the particle to go directly from its exterme position to half the amplitude.
View SolutionThe equation of a plane progressive wave is y=Asin(πt−x3). Find the value of A for which the wave speed is equal to the maximum particle speed.
View SolutionThe displacement of a particle executing SHM is given by
y=0.5 sin100t cm . The maximum speed of the particle is
View SolutionA particle is projected with a speed u at an angle θ to the horizontal. Find the radius of curvature.
At the point where the particle is at a highest half of the maximum height H attained by it.
View SolutionA particle moves in a straight line and its speed depends on time as v=|2t−3| ∫vdt representsthe distance travelled of the particle then find the displacement of the particle in 5 s
View SolutionThe equation of travelling wave is y=asin(bt+cx) then the ratio of wave velocity to maximum particle velocity is
View SolutionThe displacement of a particle executing SHM is given by y=0.25 sin(200t) cm . The maximum speed of the particle is
View SolutionA particle of mass m initially moving with speed v.A force acts on the particle f=kx where x is the distance travelled by the particle and k is constant. Find the speed of the particle when the work done by the force equals W.
View SolutionThe figure shows the force (F) versus displacement (s) graph for a particle of mass m=2kg initially at rest.
(i) The maximum speed of the particle occurs at x = …..m
(ii) The maximum speed of the particle is ….ms−1
(iii) The particle once again has its speed zero at x =....m
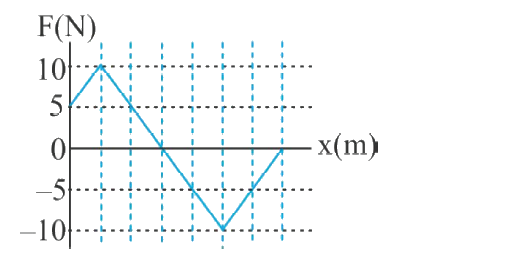
View Solution
