A particle moves in a straight line and its speed depends on time as v=|2t−3| ∫vdt representsthe distance travelled of the particle then find the displacement of the particle in 5 s
To find the displacement of the particle in 5 seconds given the speed function v=|2t−3|, we will follow these steps:
Step 1: Analyze the speed function
The speed function is given as v=|2t−3|. We need to determine when the expression inside the absolute value changes sign.
- Set 2t−3=0 to find the critical point:
2t=3⟹t=32
This means:
- For t<32, v=−(2t−3)=−2t+3
- For t≥32, v=2t−3
Step 2: Set up the integral for displacement
Displacement s can be calculated using the integral of velocity over the time interval from 0 to 5 seconds:
s=∫50vdt
We can split this integral at t=32:
s=∫320vdt+∫532vdt
Step 3: Calculate the first integral
For t in the interval (0,32):
v=−2t+3
Thus,
∫320(−2t+3)dt
Calculating this integral:
=(−t2+3t)320=(−(32)2+3⋅32)−(0)
=(−94+92)=(−94+184)=94
Step 4: Calculate the second integral
For t in the interval (32,5):
v=2t−3
Thus,
∫532(2t−3)dt
Calculating this integral:
=(t2−3t)532=(52−3⋅5)−((32)2−3⋅32)
=(25−15)−(94−92)
=10−(94−184)=10−(−94)=10+94
=404+94=494
Step 5: Combine the results
Now, we combine the results of both integrals:
s=94+494=584=292
Final Answer
The displacement of the particle in 5 seconds is:
292
The speed function is given as v=|2t−3|. We need to determine when the expression inside the absolute value changes sign.
2t=3⟹t=32
- For t<32, v=−(2t−3)=−2t+3
- For t≥32, v=2t−3
Displacement s can be calculated using the integral of velocity over the time interval from 0 to 5 seconds:
s=∫50vdt
s=∫320vdt+∫532vdt
For t in the interval (0,32):
v=−2t+3
Thus,
∫320(−2t+3)dt
=(−t2+3t)320=(−(32)2+3⋅32)−(0)
=(−94+92)=(−94+184)=94
For t in the interval (32,5):
v=2t−3
Thus,
∫532(2t−3)dt
=(t2−3t)532=(52−3⋅5)−((32)2−3⋅32)
=(25−15)−(94−92)
=10−(94−184)=10−(−94)=10+94
=404+94=494
Now, we combine the results of both integrals:
s=94+494=584=292
The displacement of the particle in 5 seconds is:
292
Topper's Solved these Questions
Similar Questions
A particle moves along a straight line its velocity dipends on time as v=4t−t2. Then for first 5s:
View SolutionThe acceleration-displacement graph of a particle moving in a straight line is as shown in figure, initial velocity of particle is zero. Find the velocity of the particle when displacement of the particle is s=12m.
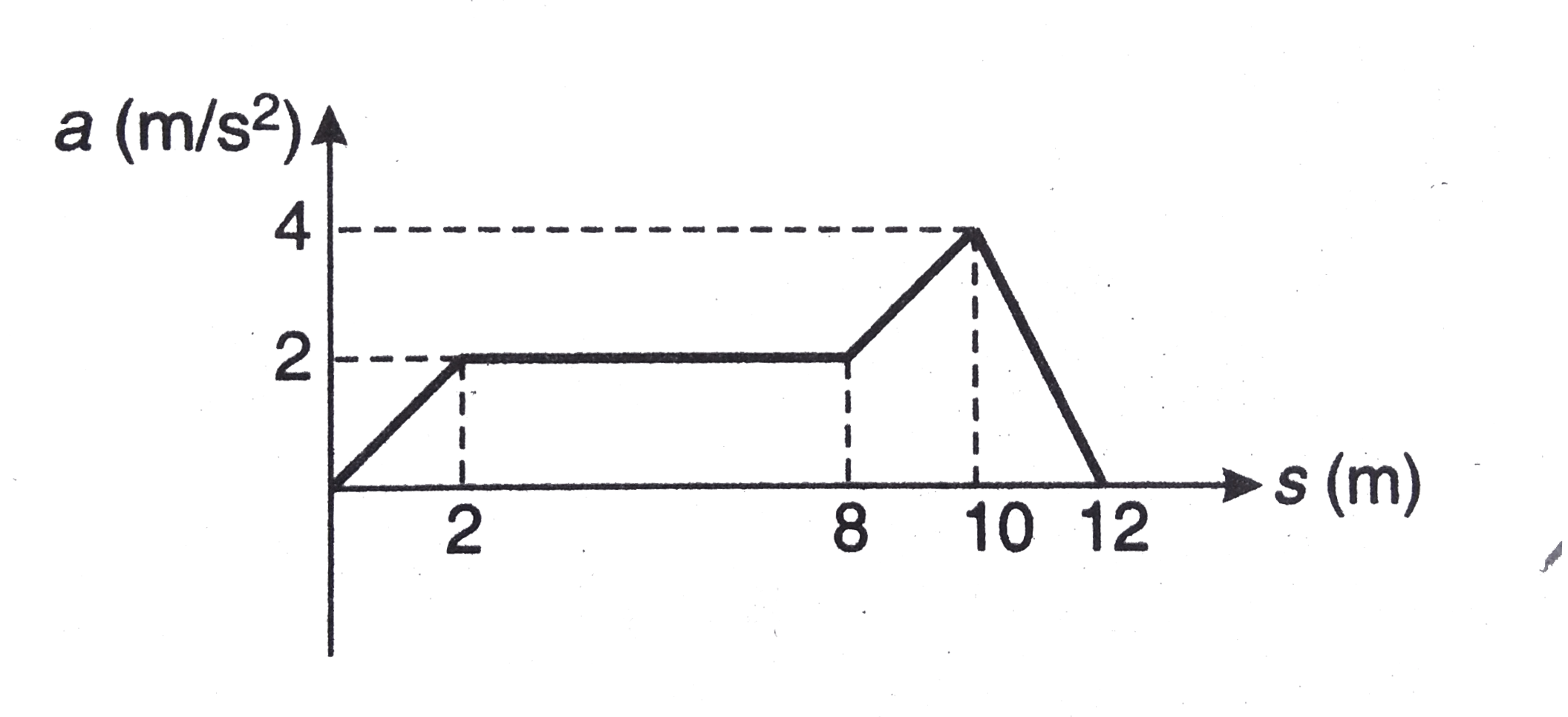
View SolutionPower of the only force acting on a particle of mass m=1 kg moving in straight line depends on its velocity as P=v2 where v is in m/s and P is in watt. If initial velocity of the particle is 1m/s, then the displacement of the particle in ln2 second will be :
View SolutionA particle of mass m initially moving with speed v.A force acts on the particle f=kx where x is the distance travelled by the particle and k is constant. Find the speed of the particle when the work done by the force equals W.
View SolutionA particle moves in a straight line with constant speed of 4m/s for 2s, then with 6m/s for 3s. Find the average speed of the particle in the given time interval.
View SolutionThe velocity-time graph of a particle moving in a staight line is shown in the . Find the displacement and the distance trav elled by the particle in 6s.
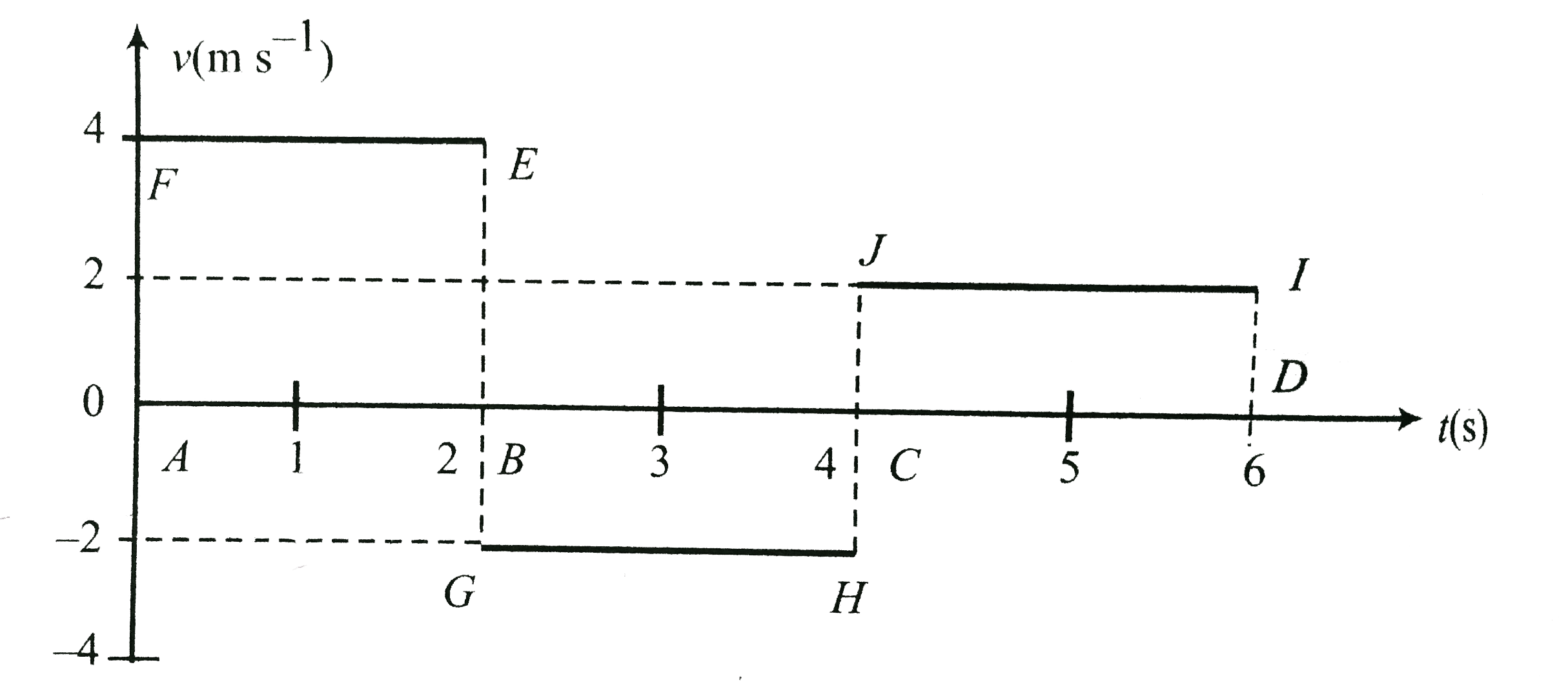 .
.
View SolutionA particle moves in a straight line from origin. Its velocity time curve is shown. Find the distance of particle at the =8sec. From the origin and the distance travelled by the particle during first 8 seconds.
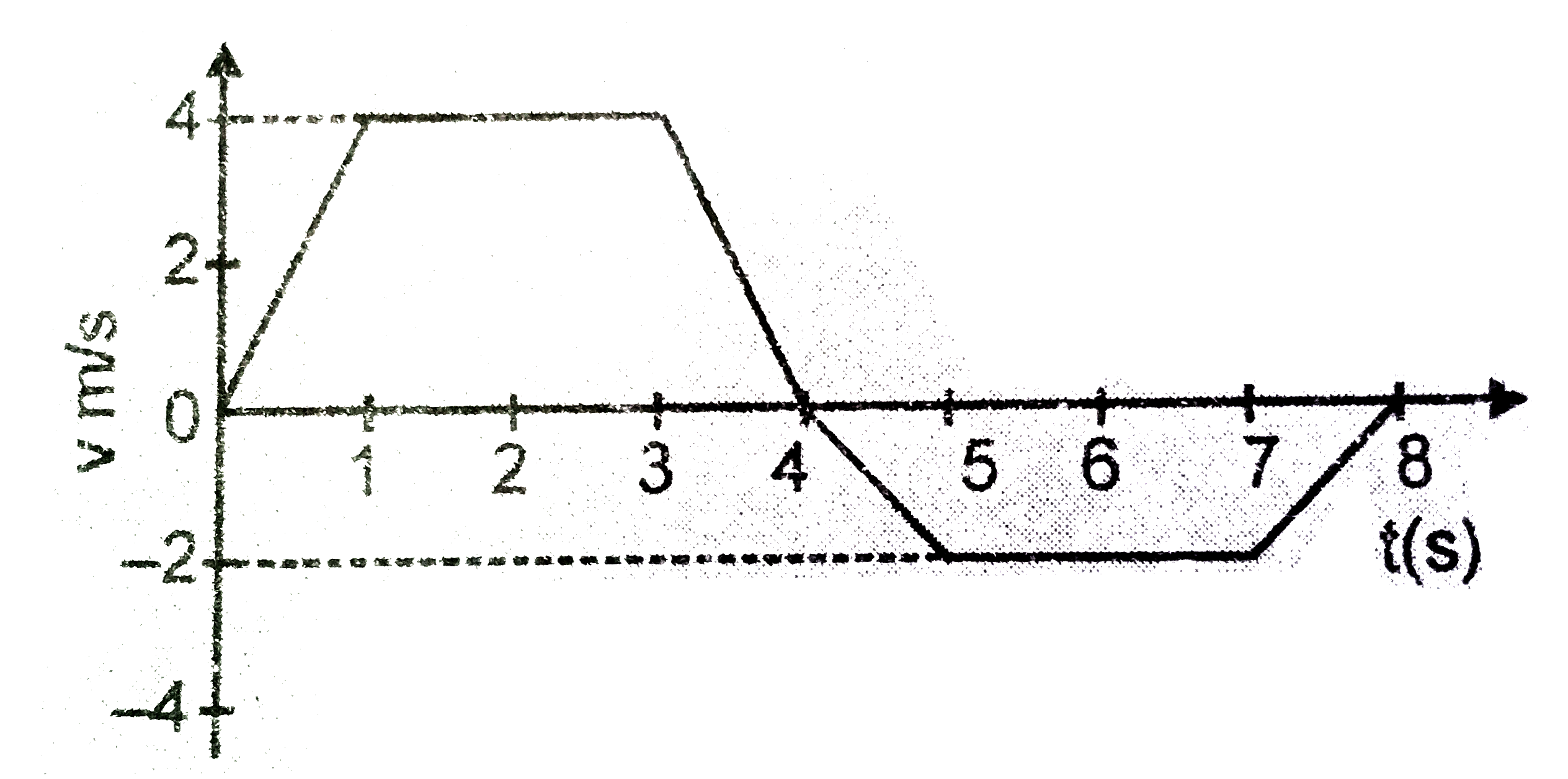
View SolutionVelocity of a particle moving along a straight line at any time 't' is give by V=cos(π3t) . Then the distance travelled by the particle in the first two seconds is :
View SolutionVelocity of a particle moving in a straight line varies with its displacement as v=(√4+4s)m/s. Displacement of particle at time t=0 is s=0. Find displacement of particle at time t=2s.
View SolutionVelocity time equation of a particle moving in a straight line is v=2t−4 for t≤2s and v=4−2t for t>2.The distance travelled by the particle in the time interval from t=0 to t=4s is (Here t is in second and v in m/s)
View Solution
