If the resultant of all external forces is zero, then velocity of centre of mass will be
zero
infinite
constant
either 'a' or 'c'
The correct Answer is:C
Step by step video, text & image solution for If the resultant of all external forces is zero, then velocity of centre of mass will be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The concept of centre of mass proves that laws of mechanics which are true for a point mass, are equally valid for all macroscopic bodies of any shape, size, mass, etc. For example, when vector sum of external forces acting on a system of particles is zero, the velocity of centre of mass of the system will remain constant.
Read the above passage and answer the following questions :
(i) Is centre of mass of a body a real point ?
(ii) Does centre of mass lie within the body always ?
(iii) How do you justify that −−→vcm= constant ?
View SolutionShow that in the absence of any external force, the velocity of the centre of mass remains constant.
View Solution
Knowledge Check
Statement 1: Two spheres undergo a perfectly elastic collision. The kinetic energy of system of both spheres is always constant. [There is no external force on system of both spheres]. Statement 2: If net external force on a system is zero, the velocity of centre of mass remains constant.
AStatement-1 is true, Statement-2: is true, Statement-2 is a correct explanation for Statement-1.BStatement-1 is true, Statement-2: is true, Statement-2 is NOT a correct explanation for Statement-1.CStatement-1 is true but statement-2 is falseDStatement-1 is false, Statement-2 is trueAccording to the principle of conservation of linear momentum, if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain, at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
Two blocks of masses 'm'and '2m' are placed as shown in Fig. There is no friction anywhere. A spring of force constant k is attached to the bigger block. Mass 'm' is kept in touch with the spring but not attached to it. 'A' and 'B' are two supports attached to '2m'. Now m is moved towards left so that spring is compressed by distance 'x' and then the system is released from rest.

Find the relative velocity of the blocks after 'm' leaves contact with the spring.A√2k3mB3x√k2mCx√3k2mDnone of theseAccording to the principle of conservation of linear momentum, if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain, at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
Two blocks of masses 'm'and '2m' are placed as shown in Fig. There is no friction anywhere. A spring of force constant k is attached to the bigger block. Mass 'm' is kept in touch with the spring but not attached to it. 'A' and 'B' are two supports attached to '2m'. Now m is moved towards left so that spring is compressed by distance 'x' and then the system is released from rest.

Now m arrives at B. Due to its inertia of motion 'm' breaks the support 'B' and due to some resistance offered by 'B' , the resulting velocity of 'm' is reduced to half of its previous value. Then what you can say about the velocity of 2m?AIt is also reduced to half of its previous valueBIt is reduced to less than half of its previous value.CIt is reduced to more than half of its previous value.DIt remains the same.
Velocity Of Centre Of Mass Of System
View SolutionIf the resultant of the following forces is zero, find the value of F0.
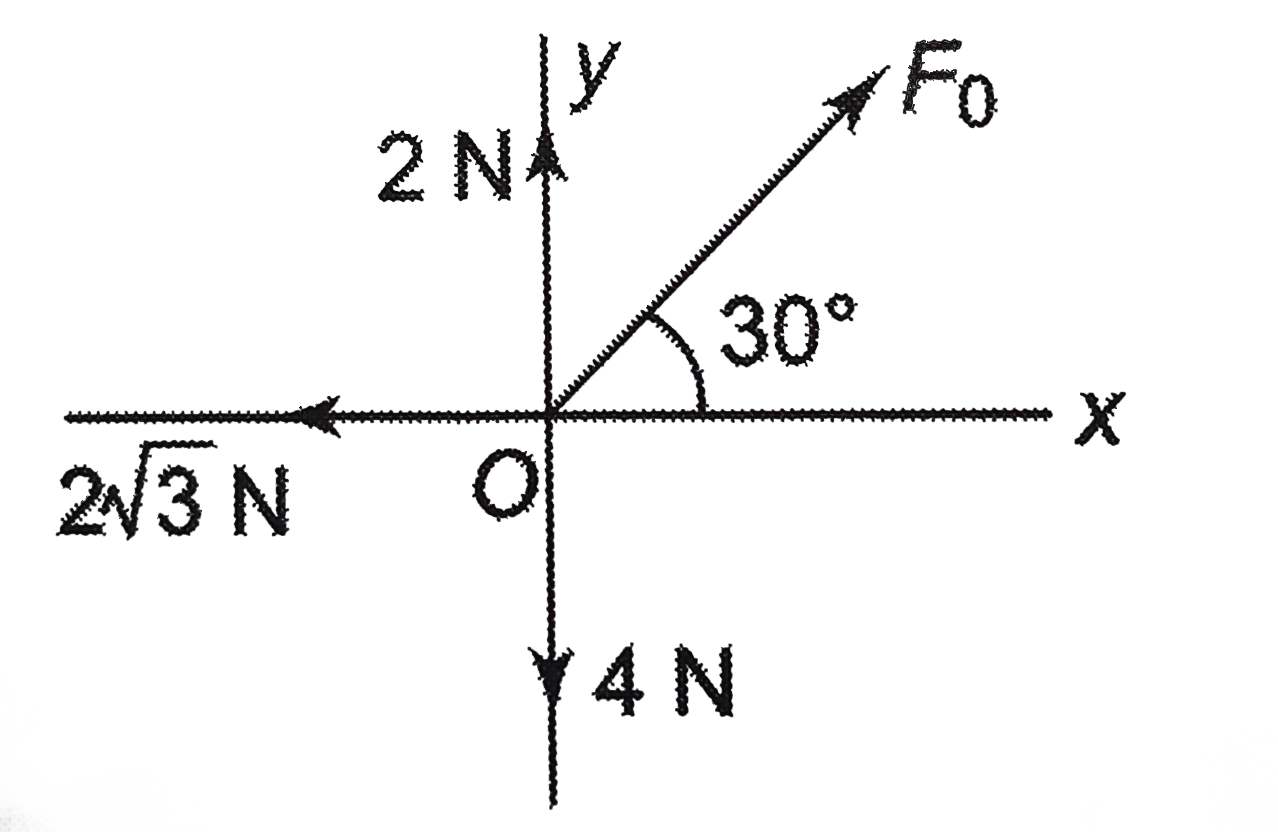
View SolutionAccording to the principle of conservation of linear momentum, if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain, at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
Two blocks of masses 'm'and '2m' are placed as shown in Fig. There is no friction anywhere. A spring of force constant k is attached to the bigger block. Mass 'm' is kept in touch with the spring but not attached to it. 'A' and 'B' are two supports attached to '2m'. Now m is moved towards left so that spring is compressed by distance 'x' and then the system is released from rest.

What is the loss in the energy of the system due to breaking of B?
View SolutionIf the net external force acting on a system is zero, then the centre of mass?
View SolutionConsider the following statements
I. If net external force on a system of particles is zero, the total linear momentum of the system will remain conserved
II. If net external force on a system of particles is zero, the velocity of the centre of mass of the system must remain constant. Choose the correct option.
View Solution
