If vector is a variable vector, whose magnitude is constant, then choose the statement which is always true.
is perpendicular to
is parallel to
is a constant vector
None of these
The correct Answer is:A
Step by step video, text & image solution for If vector a is a variable vector, whose magnitude is constant, then choose the statement which is always true. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - MCQ_TYPE
17 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - MATCH THE COLUMN
6 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Medical entranes gallery
49 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
Similar Questions
Knowledge Check
Which of the following statement is always true
AAdjoint of a symmetric matrix is symmetric matrixBAdjoint of a unit matrix is unit matrixCA (adj A) = (adj A) ADAdjoint of a diagonal matrix is diagonal matrixTwo unit vector when added give a unit vector . Then choose the correct statement.
Amagnitude the their difference is √3BMignitude of their difference is 1CAngle between the vectors is 90∘DAngle between the sum and the difference of the two vectors is 90∘The magnitude of a vector cannot be
ApositiveBzeroCnegativeDunity
If the vector product of a constant vector →OA with a variable vector →OB in a fixed plane OAB be a constant vector, then the locus of B is a. a straight line perpendicular to →OA b. a circle with centre O and radius equal to ∣∣→OA∣∣ c. a straight line parallel to →OA d. none of these
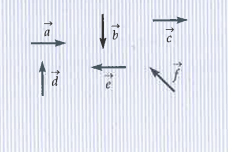
View SolutionSix vectors, →ta through →tf have the magnitudes and directions indicated in the figure. Which of the following statements is true ?
View SolutionThe magnitude of a vector cannot be
View SolutionThe magnitude of a vector cannot be :
View SolutionIf the angle between the vectors a and b be θanda⋅b=cosθ then the true statement is
View Solution
