If you carry out the integral of the electric field ∫→E.→dl for a closed path like that as shown in (Fig. 3.40), the integral will always be equal tom zero, independent of the shape of the path and independent of where charges may be located relative to the path. Explain why.
 .
.
Vf−Vi=∫fi→E.dl
In a closed path, Vi=Vf. Hence,
∫fi→E.dl in a close path will be zero.
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Exercise 3.2
9 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Exercise 3.3
9 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Examples
9 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
Statement I: no electric current will be present within a region having uniform and constant magetic field.
Statement II: Within a region of unifrom and cinstant magnetic field →B, the path integral of magnetic field ∮→B.d→l along any closed path is zero. Hence, from Ampere cirauital law ∮→B.d→l=μ0I (where the given terms ahve usual meaning), no current can be present within a region having uniform and constant magnetic field .
View SolutionA velocity filter uses the properties of electric and magnetic field to select particles that are moving with a specifice velocity. Charged particles with varying speeds are directed into the filter as shown. The filter consistt of an electric field E and a magnetic field B, each of constant magnitude, directed perpendicular to each other as shown, The charge particles will experience a force due to electric field given by F = qE. If positively charged particles are used, this force is towards right.
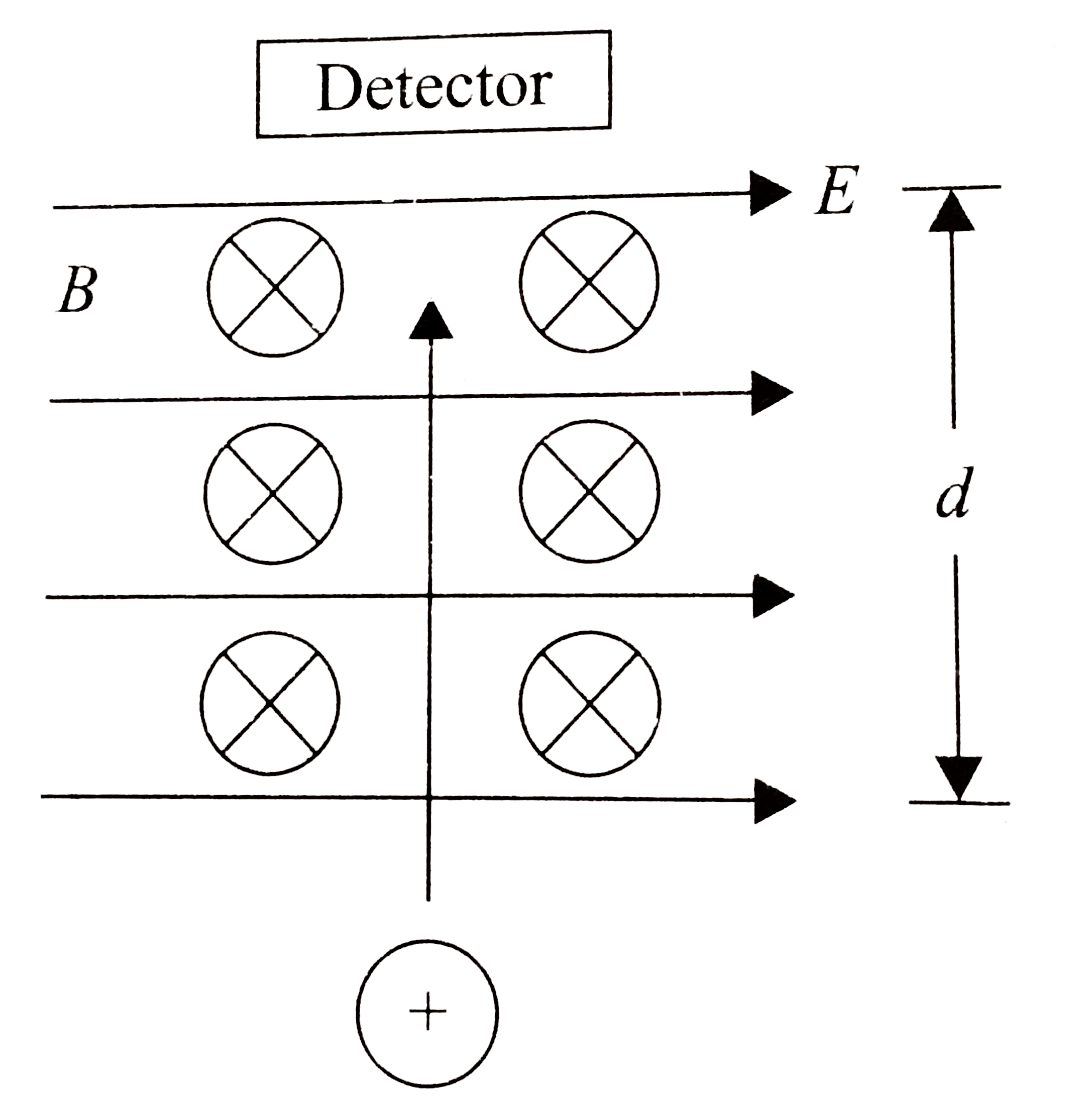
The moving particle will also experience a force due to magnetic field given by F=qvB. When forces due to the two fields are of equal magnitude, the net force on the particle will be zero, the particle will pass through centre with its path unaltered. The electric and magnetic fields can be adjusted t choose the specific velocity to be filtered. The efect of gravity can be neglected.
The electric and magnetic fields are adjusted to detect particles with positive charge q of certain speed v0. which of the following expressions is equal to this speed?
View SolutionA velocity filter uses the properties of electric and magnetic field to select particles that are moving with a specifice velocity. Charged particles with varying speeds are directed into the filter as shown. The filter consistt of an electric field E and a magnetic field B, each of constant magnitude, directed perpendicular to each other as shown, The charge particles will experience a force due to electric field given by F = qE. If positively charged particles are used, this force is towards right.
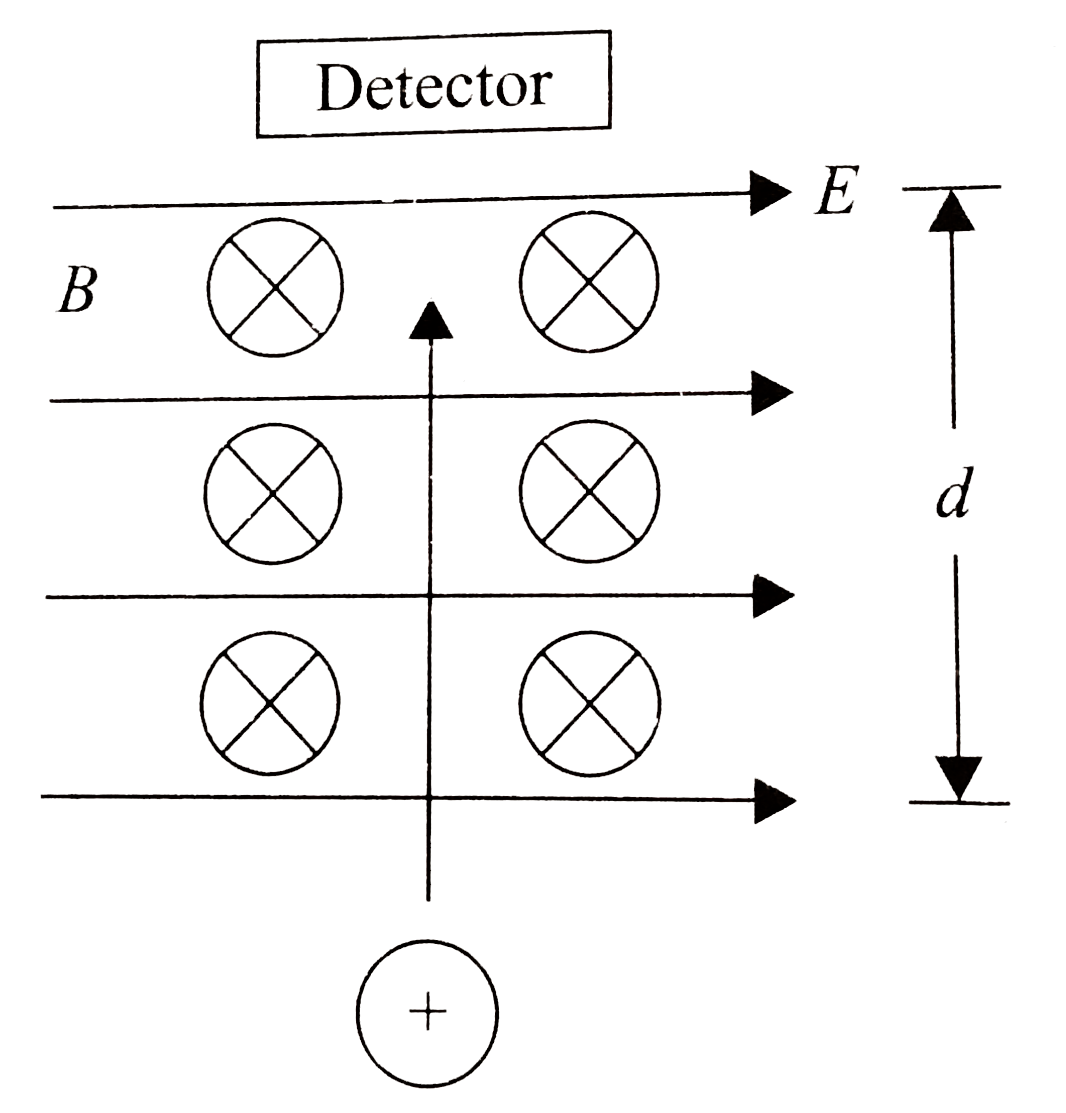
The moving particle will also experience a force due to magnetic field given by F = qvB. When forces due to the two fields are of equal magnitude, the net force on the particle will be zero, the particle will pass through centre with its path unaltered. The electric and magnetic fields can be adjusted t choose the specific velocity to be filtered. The efect of gravity can be neglected.
If the filter is set to detect particles of speed v0, which one of the following diagrams best illustrates how the magnitude of the particle acceleration (a) depends on velocity v?
View SolutionA uniform electric field E exists between two oppositely charged plates (Fig. 3.38). What will be the work done in moving a charge q along a closed rectangular path ?
 .
.
View SolutionA uniform electric field E is created between two parallel
., charged plates as shown in figure . An electron
. enters the field symmetrically between the plataes with a
. speed v_0. The length of each plate is l. Find the angle of
. deviation of the path of the electron as it comes out
. of the field.

View SolutionA uniform electric field E is created between two parallel
., charged plates as shown in figure . An electron
. enters the field symmetrically between the plates with a
. speed v_(0)'. The length of each plate is l. Find the angle of
. deviation of the path of the electron as it comes out
. of the field.

View SolutionA uniform electric field E is created between two parallel
., charged plates as shown in figure . An electron
. enters the field symmetrically between the plataes with a
. speed v_0. The length of each plate is l. Find the angle of
. deviation of the path of the electron as it comes out
. of the field.
 θ
=
tan
−
1
E
l
m
v
2
0
θ
=
tan
−
1
(
e
E
l
m
v
2
0
)
θ
=
tan
−
1
(
e
E
l
m
v
0
)
θ
=
tan
−
1
(
e
E
m
v
2
0
)
θ
=
tan
−
1
E
l
m
v
2
0
θ
=
tan
−
1
(
e
E
l
m
v
2
0
)
θ
=
tan
−
1
(
e
E
l
m
v
0
)
θ
=
tan
−
1
(
e
E
m
v
2
0
)
View SolutionThree distinct current carrying wires intersect a finite rectangular plane ABCD. The current in left wire and the loop is I1. The direction of current in left most wire and right most loop is downwards as shown in figure. The current I2 through middle wire is adjusted so that the path integral of the total magnetic field along the perimeter of the rectangle is zero, that is, ∮ABCDA→B.→dl=0. Then the current I2 is-

A. 2I1 and upwards
B. 2I1 and downwards
C. 4I1 and upwards
D. 3I1 and downwards
View SolutionThe basic idea of Quantum Mechanics is that motion in any system is quantized. The system obeys Classical Mechanics except that not every motion is allowed, only those motions which obey the Bohr-Sommerfeid Quantization.
∮→P.d→r=nh,n∈N.
where →P is the momentum, →r is the position , →r is the position vector and the integral is carried over a closed path. Assuming this is applicable to a particle of mass m moving with a constant speed in a box of lenth L having eleastic collisions with the walls of the box. Answer the following questions. (h=6.6×10−34J−sec.L=3.3A,m=10−30kg)

The allowed kinetic energy of the particle is :
View SolutionThe basic idea of Quantum Mechanics is that motion in any system is quantized. The system obeys Classical Mechanics except that not every motion is allowed, only those motions which obey the Bohr-Sommerfeid Quantization.
∮→P.d→r=nh,n∈N.
where →P is the momentum, →r is the position , →r is the position vector and the integral is carried over a closed path. Assuming this is applicable to a particle of mass m moving with a constant speed in a box of lenth L having eleastic collisions with the walls of the box. Answer the following questions. (h=6.6×10−34J−sec.L=3.3A,m=10−30kg)

The allowed momenta are given by:
View Solution
