Statement I: no electric current will be present within a region having uniform and constant magetic field.
Statement II: Within a region of unifrom and cinstant magnetic field →B, the path integral of magnetic field ∮→B.d→l along any closed path is zero. Hence, from Ampere cirauital law ∮→B.d→l=μ0I (where the given terms ahve usual meaning), no current can be present within a region having uniform and constant magnetic field .
(a) Statement I is True, Statement II is True, Statement II is correct expaination for Statement I.
(b) Statement I is True, Statement II is True, Statement II is NOT a correct expaination for Statement I.
( c) Statement I is True, Statement II is false.
( d) Statement I is False, Statement II is True.
The correct Answer is:A
To solve the given question, we need to analyze both statements and determine their validity based on the principles of electromagnetic induction and Ampere's circuital law.
1. Understanding Statement I:
- Statement I claims that "no electric current will be present within a region having a uniform and constant magnetic field."
- According to Ampere's circuital law, the line integral of the magnetic field ∮→B⋅d→l around a closed loop is related to the current I passing through that loop by the equation:
∮→B⋅d→l=μ0I
- If the magnetic field →B is uniform and constant, the line integral ∮→B⋅d→l will be zero because there is no net change in the magnetic field along a closed path.
2. Analyzing Statement II:
- Statement II states that "within a region of uniform and constant magnetic field →B, the path integral ∮→B⋅d→l along any closed path is zero."
- This is indeed true as per the properties of a uniform magnetic field. Since the magnetic field does not change in magnitude or direction, the integral evaluates to zero.
3. Connecting the Statements:
- Since ∮→B⋅d→l=0 implies μ0I=0, it follows that I=0 when →B is uniform and constant.
- Therefore, Statement I is true because it logically follows from Statement II.
4. Conclusion:
- Both statements are true, and Statement II provides a correct explanation for Statement I.
- Therefore, the correct option is that both statements are true, and Statement II is a correct explanation for Statement I.
Final Answer:
- Both Statement I and Statement II are true, and Statement II is a correct explanation for Statement I. The correct option is A.
- Statement I claims that "no electric current will be present within a region having a uniform and constant magnetic field."
- According to Ampere's circuital law, the line integral of the magnetic field ∮→B⋅d→l around a closed loop is related to the current I passing through that loop by the equation:
∮→B⋅d→l=μ0I
- If the magnetic field →B is uniform and constant, the line integral ∮→B⋅d→l will be zero because there is no net change in the magnetic field along a closed path.
- Statement II states that "within a region of uniform and constant magnetic field →B, the path integral ∮→B⋅d→l along any closed path is zero."
- This is indeed true as per the properties of a uniform magnetic field. Since the magnetic field does not change in magnitude or direction, the integral evaluates to zero.
- Since ∮→B⋅d→l=0 implies μ0I=0, it follows that I=0 when →B is uniform and constant.
- Therefore, Statement I is true because it logically follows from Statement II.
- Both statements are true, and Statement II provides a correct explanation for Statement I.
- Therefore, the correct option is that both statements are true, and Statement II is a correct explanation for Statement I.
- Both Statement I and Statement II are true, and Statement II is a correct explanation for Statement I. The correct option is A.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Linked Comprehension36videos
ELECTROMAGNETIC INDUCTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Integer9videos
ELECTROMAGNETIC INDUCTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Multiple Correct23videos
ELECTROMAGNETIC INDUCTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q2videos
ELECTRICAL MEASURING INSTRUMENTS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.315videos
ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYS
Similar Questions
A: In any magnetic field region the line integral ∮→B.→dl along a closed loop is always zero.
R: The magnetic field →B in the expressioin ∮→B.→dl is due to the currents enclosed only by the loop.View SolutionIn a region where both non-zero uniform electric field and magnetic field coexist, the path of a charged particle
View Solution
Knowledge Check
- Question 1 - Select One
The torque and magnetic potential energy of a magnetic dipole in most stable position ina uniform magnetic field →B having magnetic moment →m will be
A−mB,zeroBmB,zeroCzero,mBDzero,−mB
The magnetic flux linked with a vector area →A in a uniform magnetic field →B is
View SolutionStatement I: If electric potential in certain region is constant, then the electric field must be zero in this region.
Statement II: →E=−dVdrˆv.View SolutionAn electron does not suffer any deflection while passing through a region of uniform magnetic field. What is the direction of the magnetic field ?
View SolutionIf →B1,→B2 and →B3 are the magnetic field due to l1,l2 and l3, then in Ampere's circuital law ∮→B.→dl=μ0l,→B is
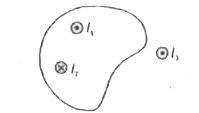 View Solution
View SolutionWhat is the direction of the force acting on a charged particle q, moving with a velocity →v a uniform magnetic field →B ?
View SolutionIf for an Amperian loop ∮→B.→dl=0 does that mean →B=0 at every point on the Amperian loop ?
View SolutionA rectangular coil is placed in a region having a uniform magnetic field B perpendicular to the plane of the coil. An emf will not be induced ion the coil if the
 View Solution
View Solution

