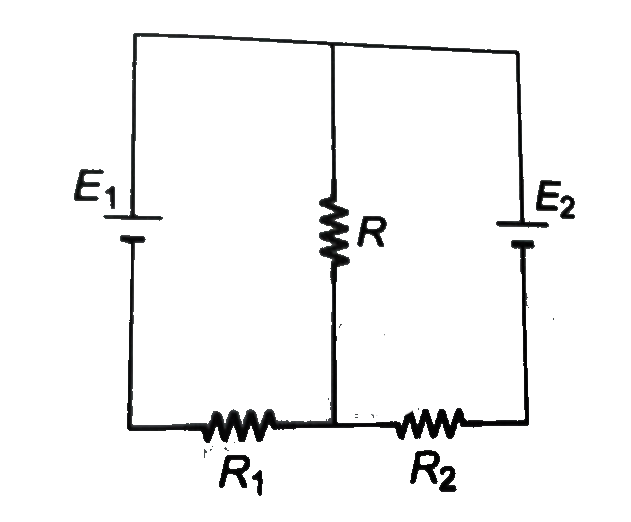
In a circuit shown in Fig, resistances and are known , as well as emf's and . The internal resitances of the sources are negatible. At what value of the resitance will teh thermal power generated in it be the highest ? What is it equal to ?
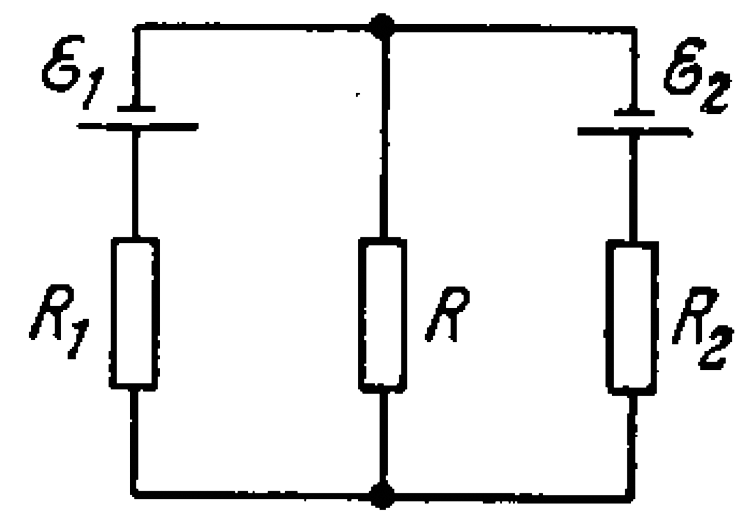
Indicate the currents in the circuit as shown in the fig.
Appying loop rule in the closed loop we get
....(1)
and in the loop , .....(2)
.....(2)
Solving (1) and (2) we get,
So, thermal power genereated in the resistance .
For to be maximum, , which fields
Hence,

Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Constant Magnetic Fiels - Magnetics
69 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electromagnetic Induction
84 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Capacitance - Energy Of An Electric Field
46 Videos
- ELECTRICITY AND MAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions
6 Videos
- ELECTROMAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions
24 Videos
Similar Questions
In a circuit shown in figure if the internal resistance of the sources are negligible then at what value of resistance R will the thermal power generated in it be the maximum. What is its value in ohms ?
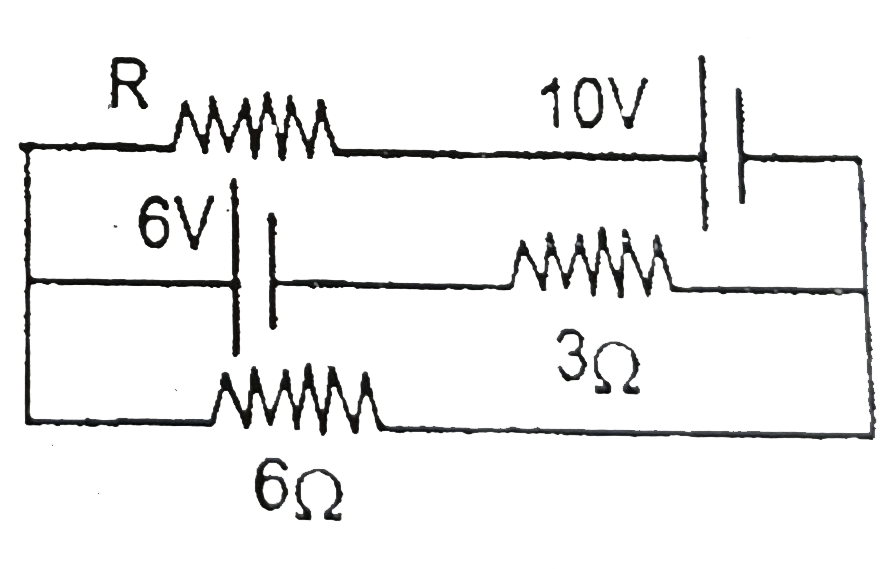
View SolutionIn a circuit shown in figure if the internal resistances of the sources are negligible then at what value of resistance R will the thermal power generated in it will be the maximum. What is the value of maximum power?
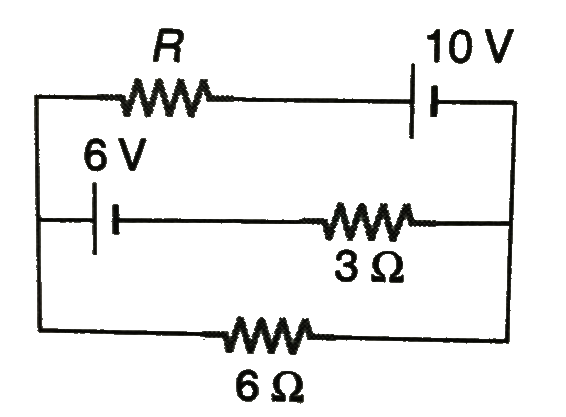
View Solution
Knowledge Check
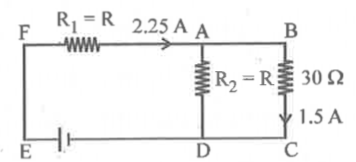
In the circuit shown in the given figure, the resistances R1andR2 are respectively
 A14Ωand40ΩB40Ωand44ΩC40Ωand30ΩD14Ωand30Ω
A14Ωand40ΩB40Ωand44ΩC40Ωand30ΩD14Ωand30Ω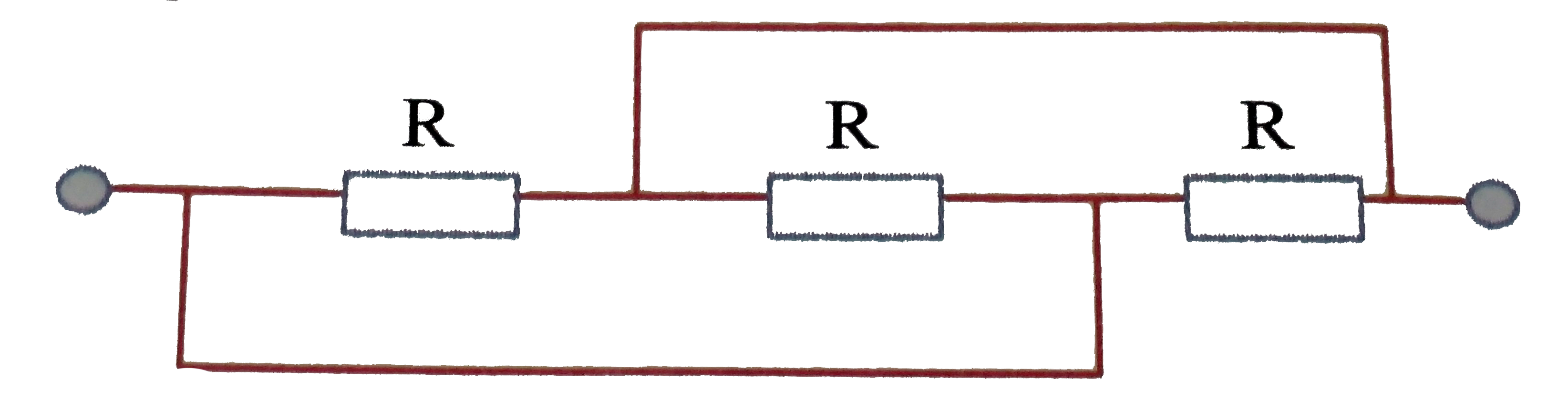
A dc source with internal resistance R0 is loaded with three identical resistance R as shown in the figure. At what value of R will the thermal power generated in this circuit be the highest?AR=2R0BR=3R0CR=R03DR=R0
In the circuit shown in figure, the emfs of batteries are E1, and E2 which have internal resistances R1, and R2. At what value of the resistance R will the thermal power generated in it be the highest? What it is?
View SolutionIn the cirucit (figure6.3) resistance R1andR2 are known and cells ar of emf e1ande2 and negligible internal resistance. At what value of R will the thermal power generated in it be the highest? What is it equal to?
View SolutionIn the given circuit if the internal resistance of the batteries are negligible, then for what value of resistance R(inΩ) will the thermal power generated in it be maximum.

View SolutionWhat is the value of the resistance R1 in the following circuit ?
View SolutionIn the circuit shown in Fig. emfE , a resistance R, and coil inductances L1 and L2 are known. The internal resistance of the source and the coil resistances are neglible. Find the steady-state currents in the coils after the swich Sw was shorted.

View SolutionA cell develops the same power across two resistances R1 and R2 separately. The internal resistance of the cell is
View Solution
