In a cylindrical region of radius a, magnetic field exists along its axis but the direction of magnetic field is opposite in the four quadrants of the region as shown in Fig. A or AB rotates with its end A at the centre of magnetic field and other end B slides on a smooth wire at the periphery of the region of magnetic field. At t = 0 the rod was situated along the +X direction.
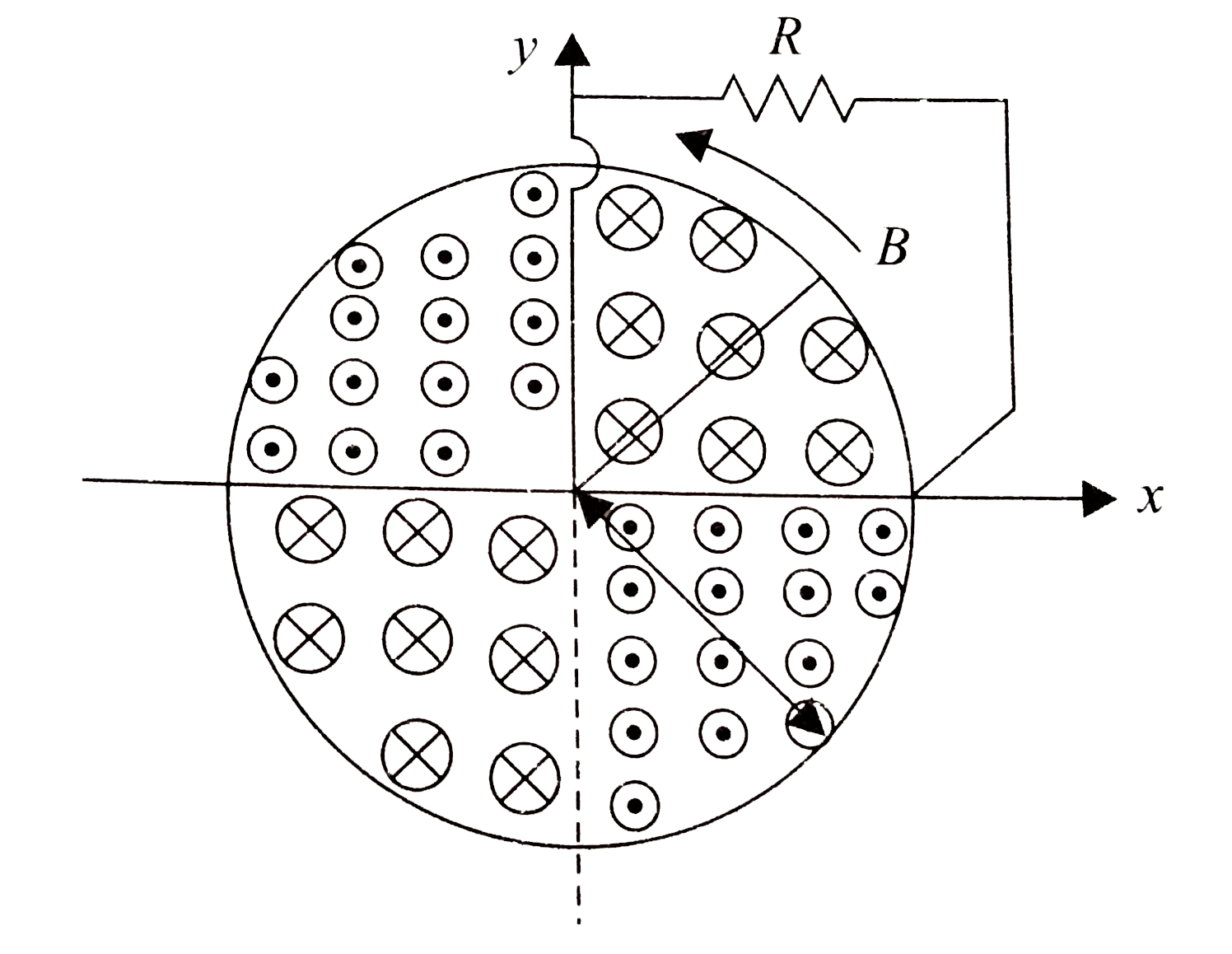
Find and plot the time dependence of the thermal power in the resistance R when rod rotates with a constant angular acceleration (α)


None of these
The correct Answer is:A
(a) When rod rotates with constant angular speed ω.
e=±12B(a)(aω)=±12Ba2ω
∴i=eR=±Ba2ω2R
so, for t=0→T4,T2→3T4 and so on, i=−Ba2ω2R
The i-t graph is as shown in fig. the i-t equation can be written as,
i=12R(−1)n+1Ba2ω
where n=1,2,3...andtn=nπ2ω
Here positive current means current from left to right through the resistance and vice-versa.
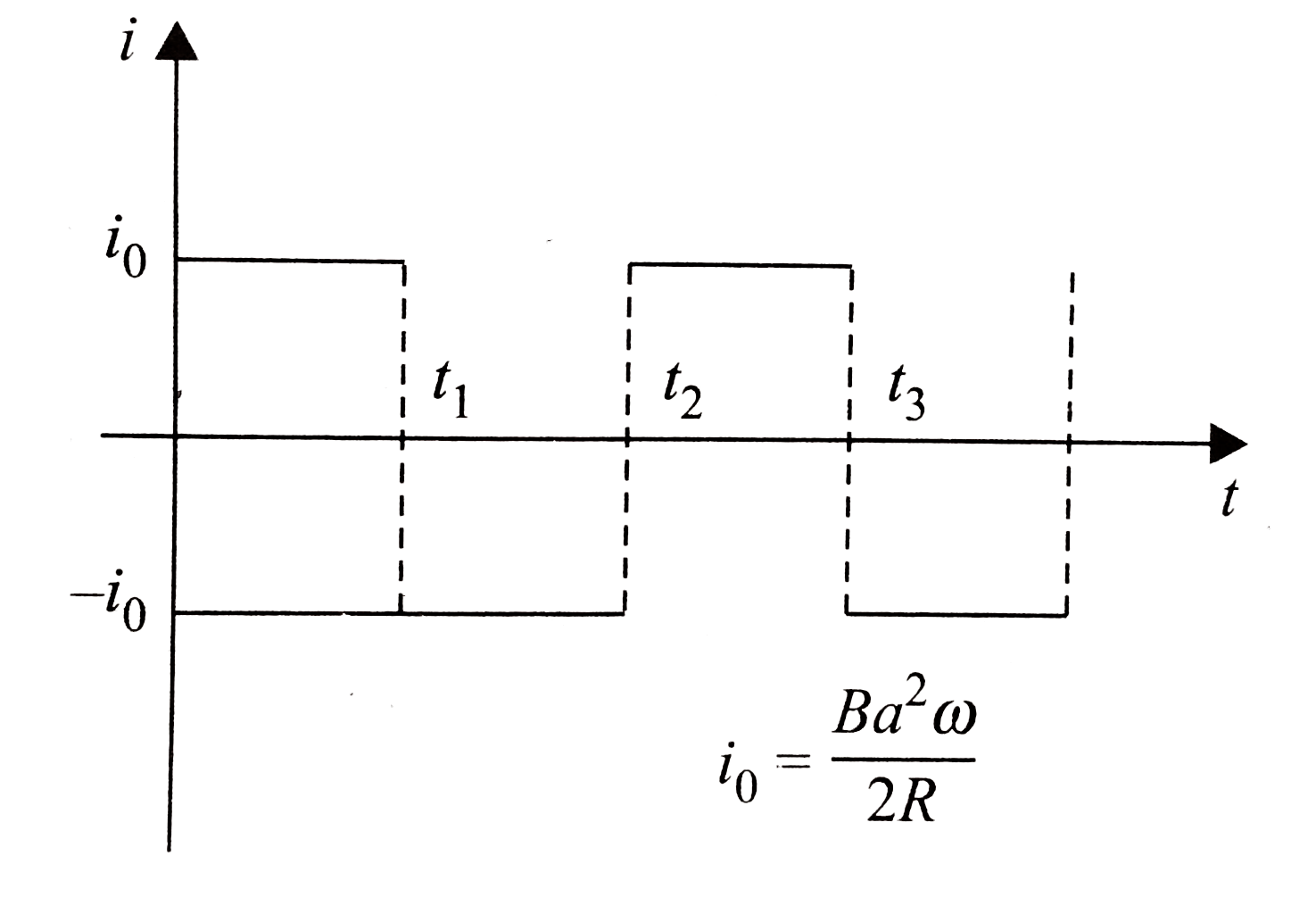
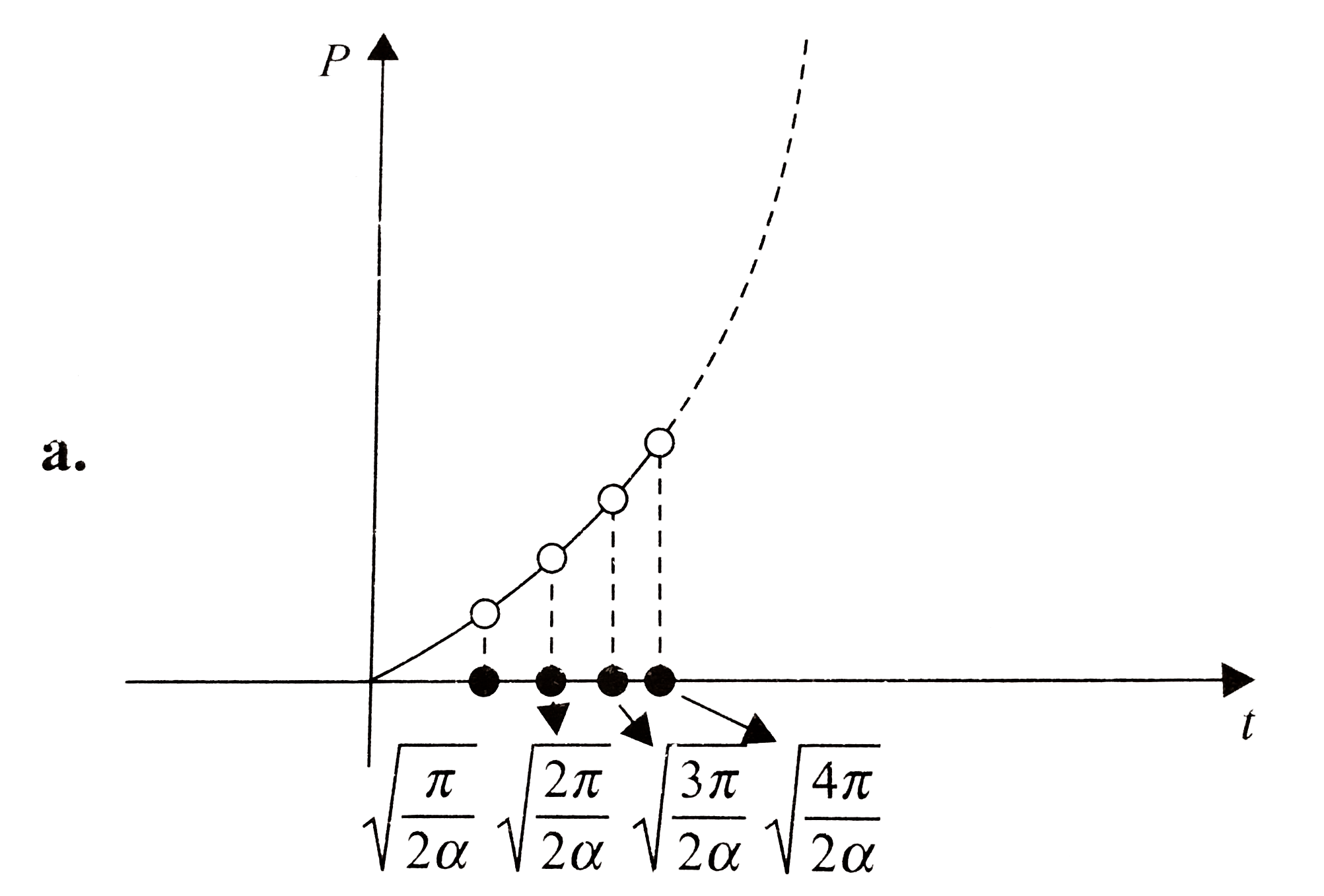
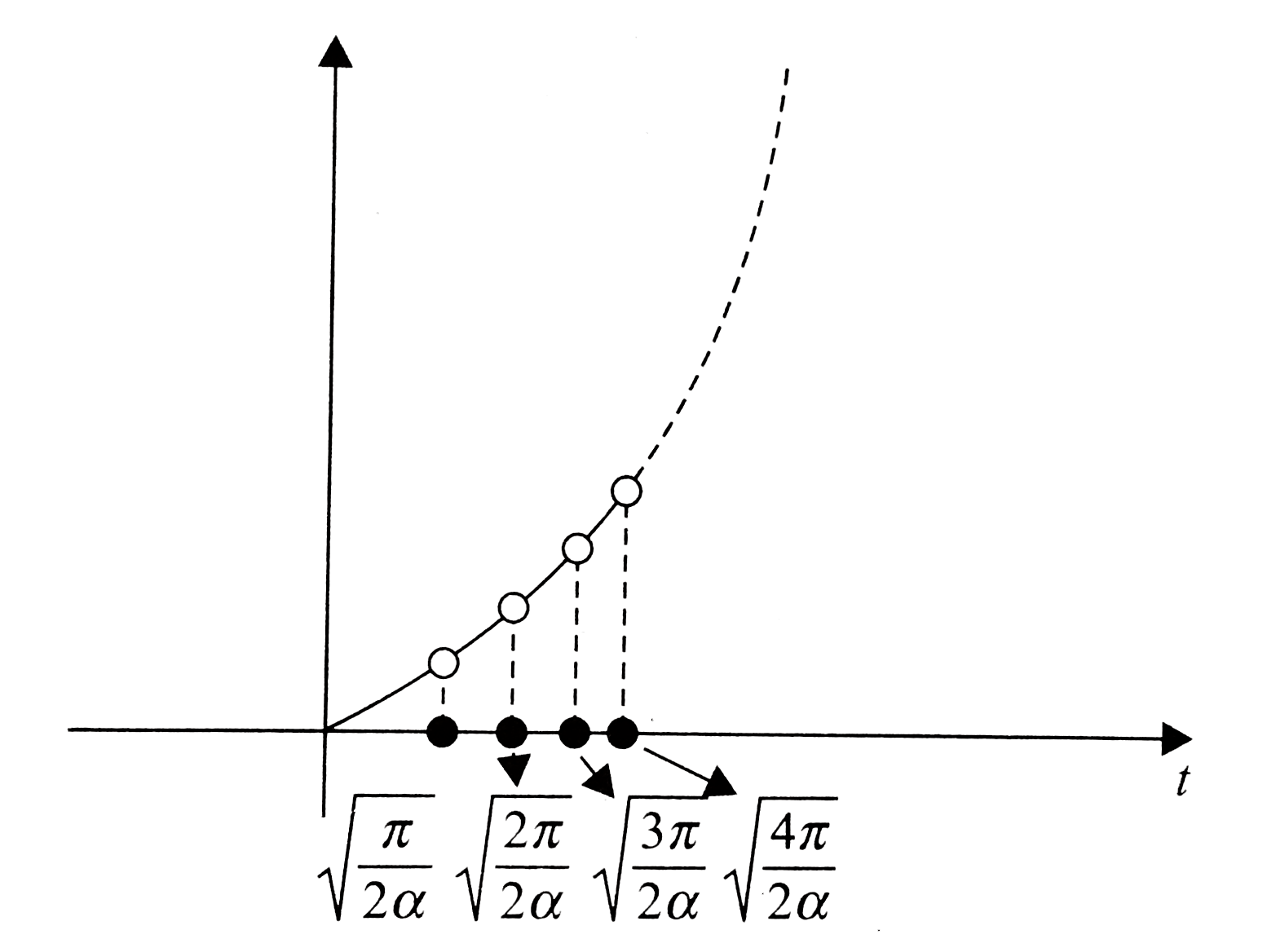
(b) α = constant.
ω=αt
ε=bωl22=(Bl22)α⋅t,I=ER=[Bl2α2R]⋅t
I is negative in quardrant I
I is positive in quadrant II
I is negative in quadrant III
I is positive in quadrant IV

also, t1/4,t1
12αt214,t1/4=√π2α
t1/2=√2π2α,t3/4=√3π4α×2=√3π2α
√3−√2−√1
PR=I2R=[Bl2α2R]2⋅R⋅t2P∝t2,y=ax2
Except at √π2α,√2π2α,...√nπ2α(≠ψlonN)
where P=0
 .
.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer12videos
MISCELLANEOUS VOLUME 5
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Multiple Correct34videos
MISCELLANEOUS VOLUME 5
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False3videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - ddp.5.514videos
NUCLEAR PHYSICS
Similar Questions
In a cylindrical region of radius a, magnetic field exists along its axis but the direction of magnetic field is opposite in the four quadrants of the region as shown in Fig. A or AB rotates with its end A at the centre of magnetic field and other end B slides on a smooth wire at the periphery of the region of magnetic field. At t=0 the rod was situated along the +X direction.
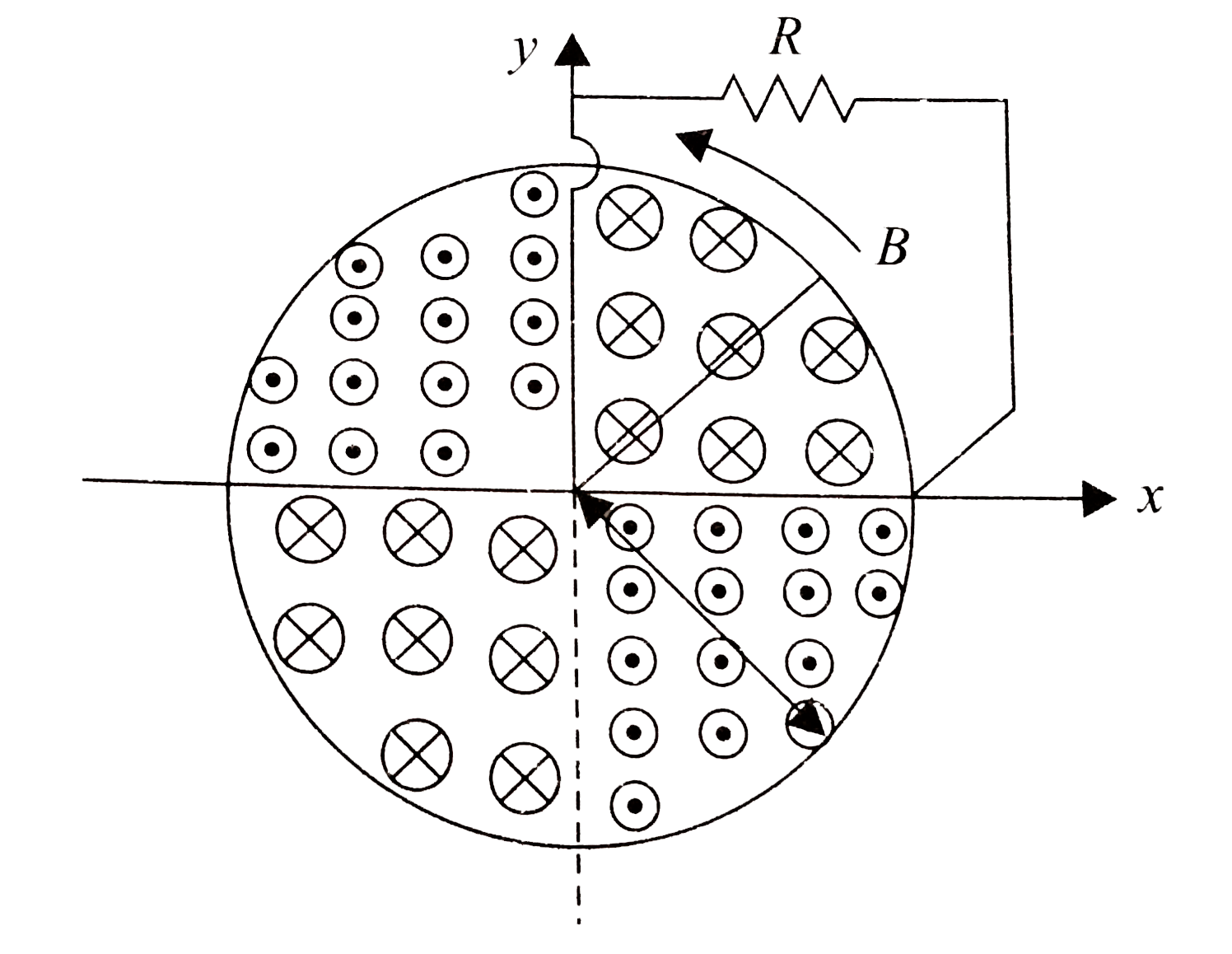
Find and plot the time dependence of the current in the resistance R when rod rotates with a constant angular velocity (ω).View SolutionIn a cylindrical region of radius a, magnetic field exists along its axis but the direction of magnetic field is opposite in the four quadrants of the region as shown in Fig. A or AB rotates with its end A at the centre of magnetic field and other end B slides on a smooth wire at the periphery of the region of magnetic field. At t = 0 the rod was situated along the +X direction.
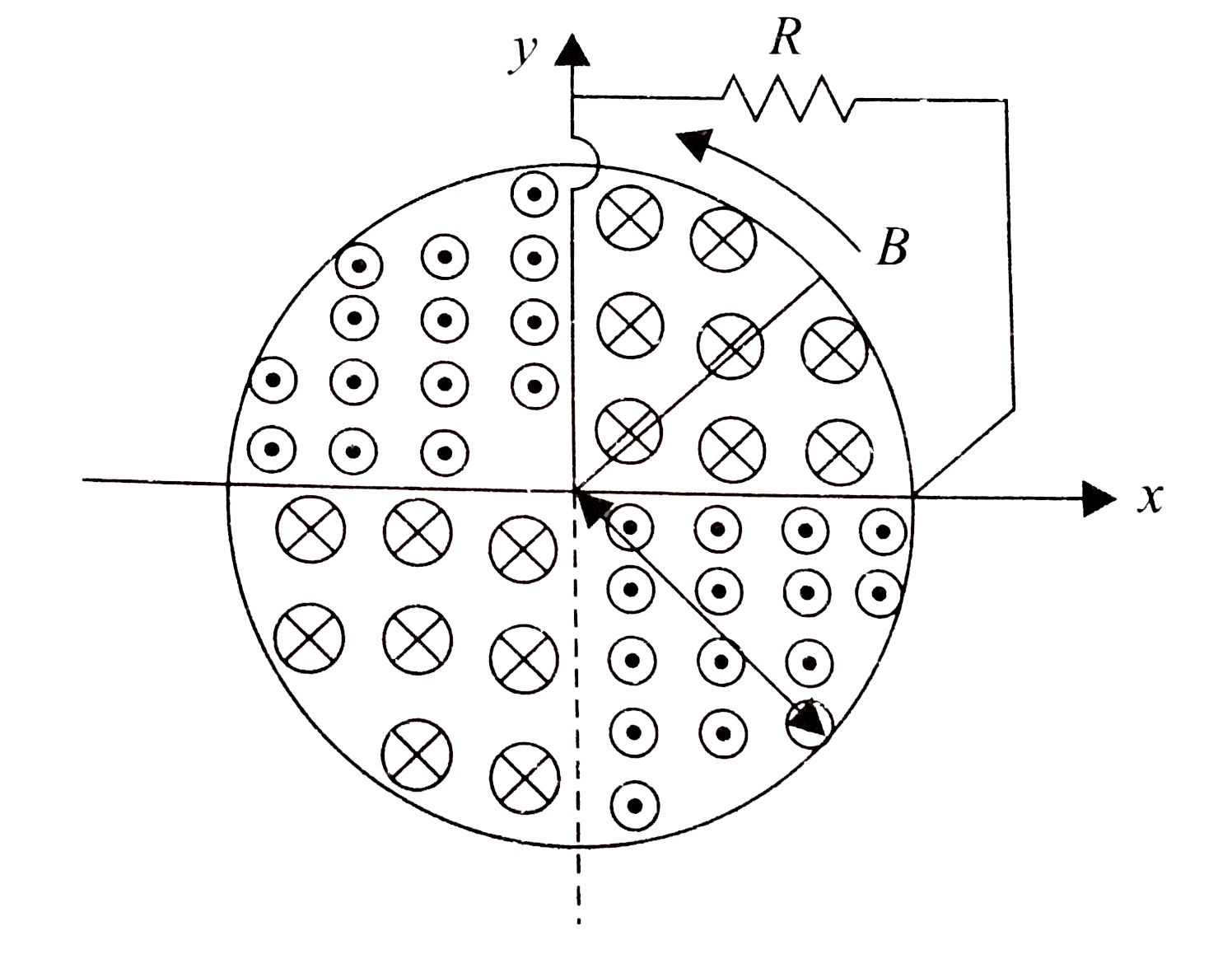
Find and plot the time dependence of the current in the resistance R when rotates with a constant angular acceleration (α)View SolutionB0 is the magnetic field at point P for a given straight wire as shown in figure. If this wirre is bent into a circular loop, then magnetic field at the centre of loop is
_PHY_E06_130_Q01.png) View Solution
View SolutionA magnetic of magnetic moment placed along the X-axis in an magnet field .Find the torque acting on the magnetic field
View SolutionMagnetic field in cylindrical region of radius R in inward direction is as shown in figure.
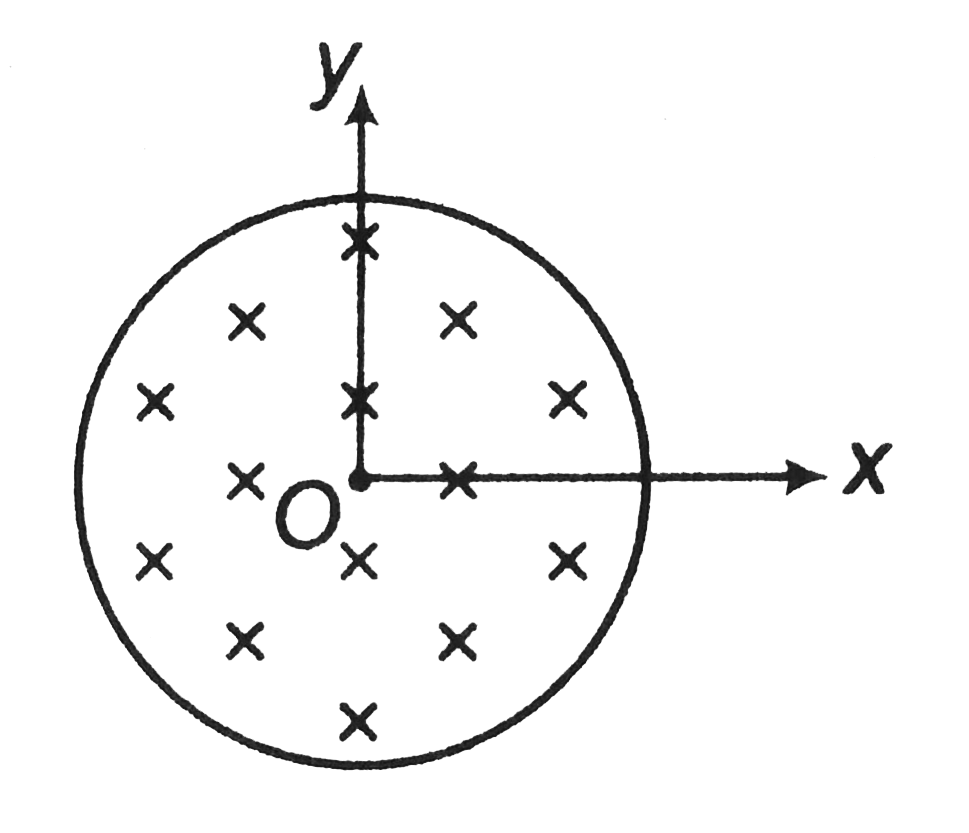 View Solution
View SolutionAn electron beam projected along + X-axis, experience a force due to a magnetic field along the + Y-axis. What is the direction of the magnetic field?
View SolutionThe region around a magnet where its influence is felt is called magnetic field.
View SolutionA uniform but increasing with time magnetic field exists in as cylindrical region. The direction of force on an electron at P as
 View Solution
View SolutionIn a cylindrical region uniform magnetic field which is perpendicular to the plane of the figure is in increasing with time and a conducting rod PQ is placed in the region.If C is the centre of the circle then
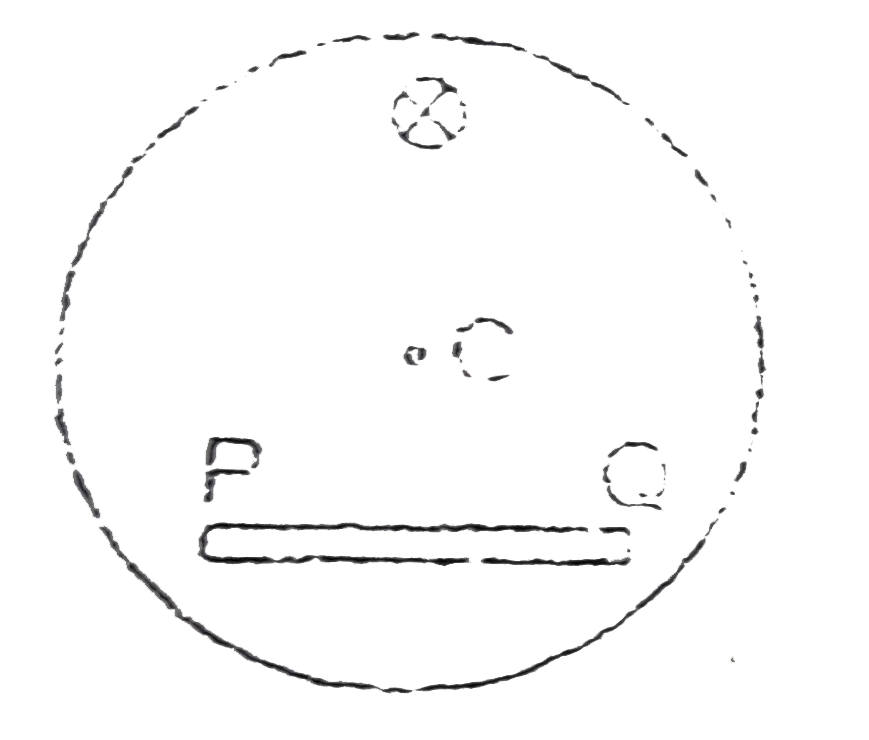 View Solution
View SolutionA uniform electric field and a uniform magnetic field are acting along the same direction in a certain region. If an electron is projected along the direction of the fields with a certain velocity then
View Solution
