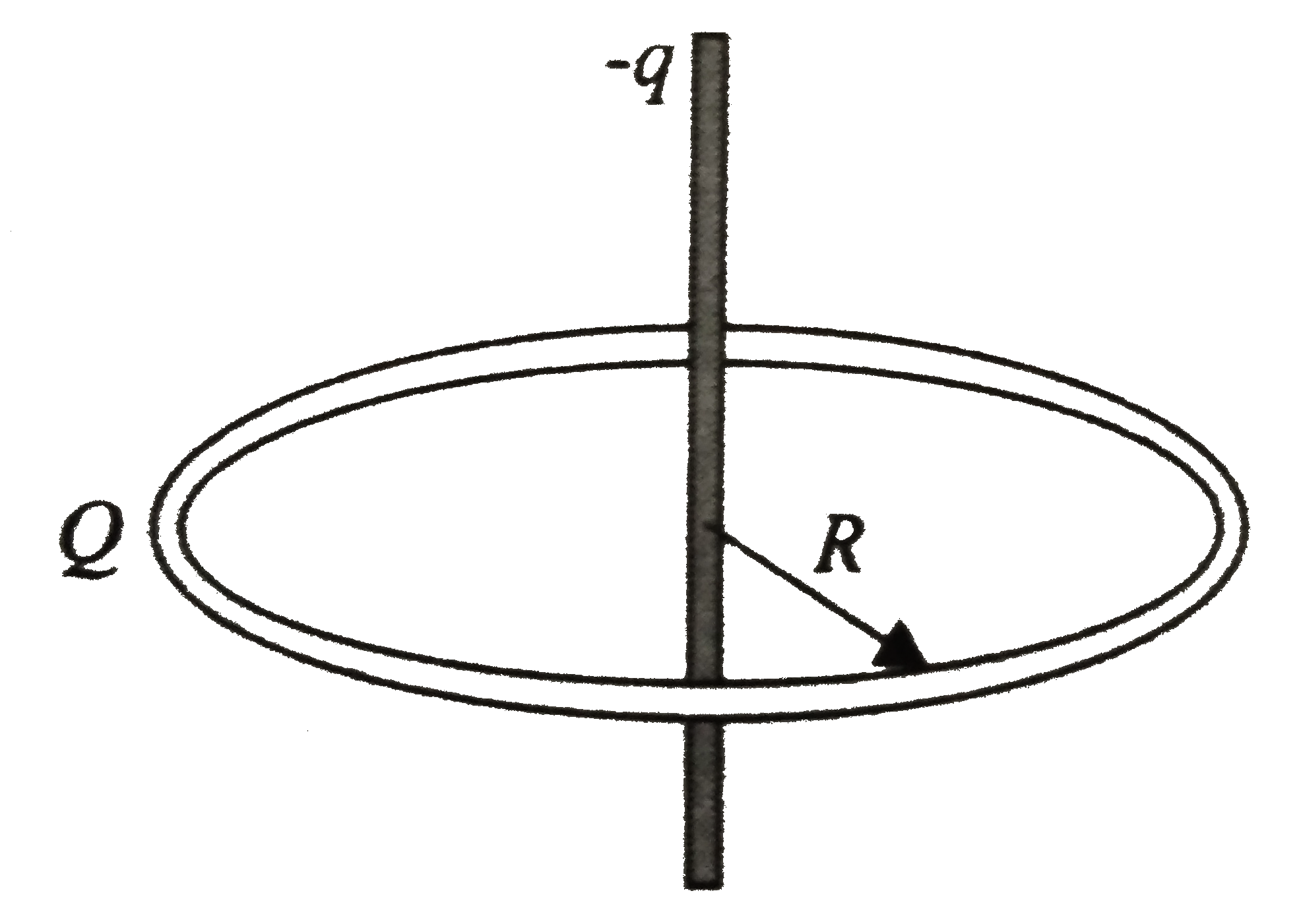
In a free space, a thin rod carrying uniformly distributed negative charge is placed symmetrically along the axis of a tin ring of radius R varrying uniformly dostributed charge Q. The mass of the rod is m and length is . The ring is fixed and the rod is free to move. The rod is displaced slightly along the axis of the ring and then released. Find the period T to the small amplitude oscillations of the rod.
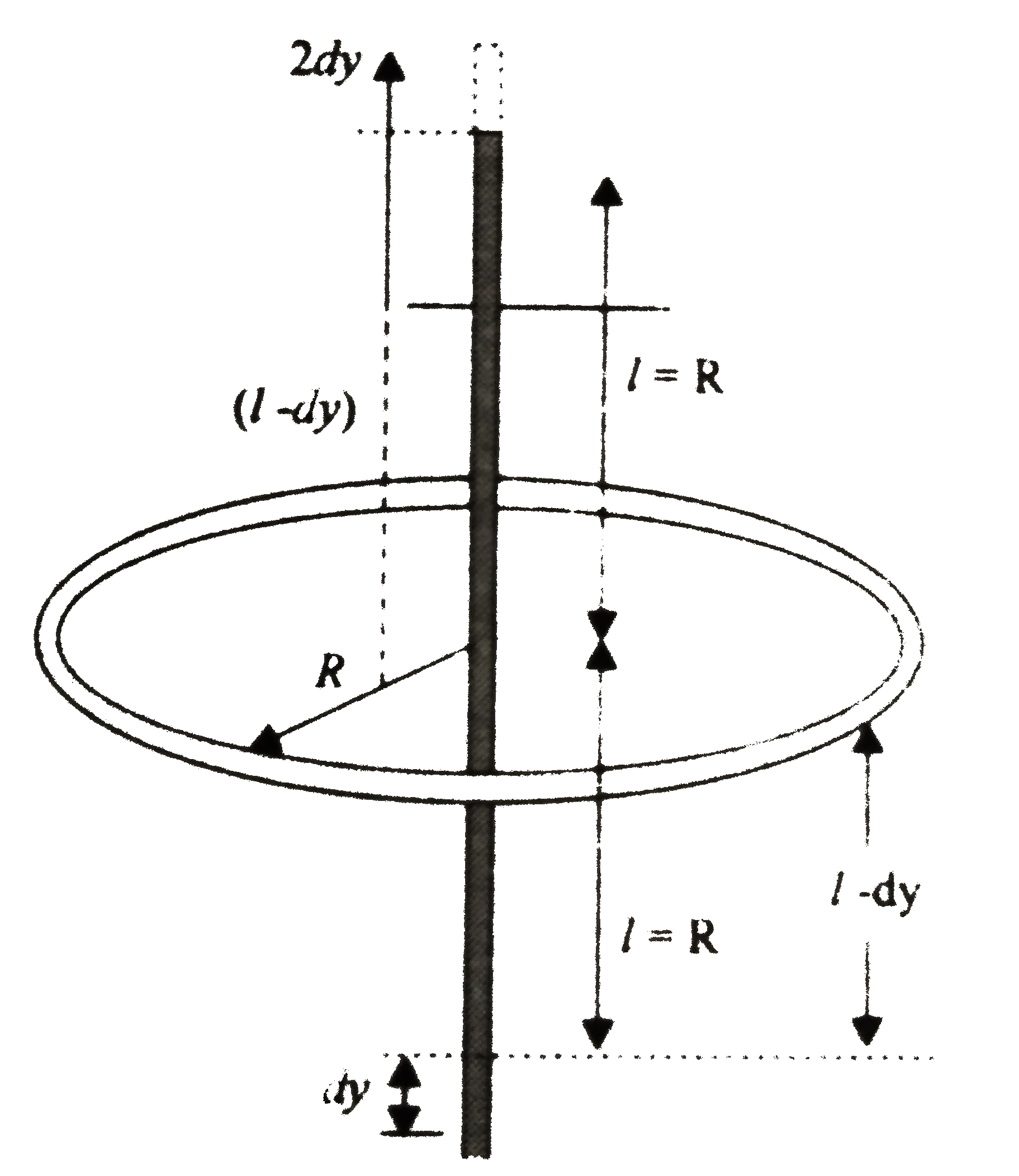
If we displace the rod by length upward the unbalaced force will be due to length 2 dy. Hence the unbalanced force on the element is
Hence,
or
or
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Exercises
58 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Subjective
32 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Answer Correct Type
22 Videos
- COMMUNICATION SYSTEMBOOK - CENGAGE PHYSICSCHAPTER - COMMUNICATION SYSTEMEXERCISE - QUESTION BANK
19 Videos
- Current ElectricityBOOK - CENGAGE PHYSICSCHAPTER - Current ElectricityEXERCISE - QUESTION BANK
40 Videos
Similar Questions
Knowledge Check
two identical rings of radius R have uniformly distributed charge Q(Q>0) each. Both the rings are fixed and are placed coaxially separated by a distance of R. if a small positive point charge is placed at the mid point and is displaced slightly along the axis then,
Ait will not perform oscillationBit will perform oscillation but no SHMCit will perform SHMDanswer will depend on the magnitude of the charge.Charges q is uniformly distributed over a thin half ring of radius R. The electric field at the centre of the ring is
Aq2π2ε0R2Bq4π2ε0R2Cq4πε0R2Dq2πε0R2A ring of radius R is charged uniformly with a charge +Q. The potential at a point on its axis at a distance 'r' from any point on ring will be-
AkQ√R2+r2BkQrCkQ(r2+R2)3/2DkQr2(r2−R2)1/2
A ring of radius R carries a uniformly distributed charge +Q. A point charge −q is placed on the axis of the ring at a distance 2R from the centre of the ring and released from rest. The particle executes a ismple harmonic motion along the axis of the ring.
View SolutionPotential on the axis of ring of radius 3R and at distance 4R from centre of ring is (charge on the ring is Q )
View SolutionA thin straight rod of length l carrying a uniformly distributed charge q is located in vacuum. Find the magnitude of the electric force on a point charge 'Q' kept as shown in the figure.

View SolutionA point charge q is located at the centre fo a thin ring of radius R with uniformly distributed charge −q, find the magnitude of the electric field strength vectro at the point lying on the axis of the ring at a distance x from its centre, if x>>R.
View SolutionA ring of radius R with a uniformly distributed charge q as shown in figure. A charge q0, is now placed at the centre of the ring. Find the increment in-the tension in ring.

View Solution
