In a galvanometer 5% of the total current in the circuit passes through it. If the resistance of the galvanometer is G, the shunt resistance 'S' connected to the galvanometer is
19
G/19
20 G
G/20
The correct Answer is:B
To find the shunt resistance S connected to a galvanometer, we can follow these steps:
1. Understand the Current Distribution:
- Let the total current in the circuit be I.
- The current passing through the galvanometer IG is given as 5% of the total current I.
- Therefore, we can express IG as:
IG=5100×I=I20
2. Determine the Current through the Shunt:
- The current flowing through the shunt resistance S is the remaining current after the galvanometer:
IS=I−IG=I−I20=20I20−I20=19I20
3. Apply Kirchhoff’s Law:
- According to Kirchhoff's law, the potential difference across the galvanometer and the shunt must be equal. Therefore:
IG⋅G=IS⋅S
- Substituting the values of IG and IS:
(I20)⋅G=(19I20)⋅S
4. Rearranging the Equation:
- We can rearrange the equation to solve for S:
S=IG⋅GIS=(I20)⋅G(19I20)
- The I terms cancel out:
S=G19
5. Conclusion:
- The shunt resistance S connected to the galvanometer is:
S=G19
Final Answer:
The shunt resistance S is G19.
---
- Let the total current in the circuit be I.
- The current passing through the galvanometer IG is given as 5% of the total current I.
- Therefore, we can express IG as:
IG=5100×I=I20
- The current flowing through the shunt resistance S is the remaining current after the galvanometer:
IS=I−IG=I−I20=20I20−I20=19I20
- According to Kirchhoff's law, the potential difference across the galvanometer and the shunt must be equal. Therefore:
IG⋅G=IS⋅S
- Substituting the values of IG and IS:
(I20)⋅G=(19I20)⋅S
- We can rearrange the equation to solve for S:
S=IG⋅GIS=(I20)⋅G(19I20)
- The I terms cancel out:
S=G19
- The shunt resistance S connected to the galvanometer is:
S=G19
The shunt resistance S is G19.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-III49videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IB71videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question15videos
MOTION IN A STRAIGHT LINE
- BOOK - AAKASH SERIESCHAPTER - NUCLEAR PHYSICSEXERCISE - ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions3videos
NUCLEAR PHYSICS
Similar Questions
Knowledge Check
- Question 1 - Select One
If the galvanometer current is 10 mA, resistance of the galvanometer is 40Ω and shunt of 2Ω is connected to the galvanometer, the maximum current which can be measured by this ammeter is
A0.21AB2.1AC210AD21A
In Q.36, the combined resistance of the shunt and the galvanometer is
View SolutionIf 2% of the main current is to be passed through the galvanometer of resistance G, the resistance of shunt required is
View SolutionThe senstivity of a galvanometer that measures current is decreased by 1/40 times by using shunt resistance of 10Ω . Then, the value of the resistance of the galvanometer is
View SolutionThe value of current in the given circuit if the ammeter is a galvanometer with a resistance RG=50Ω is
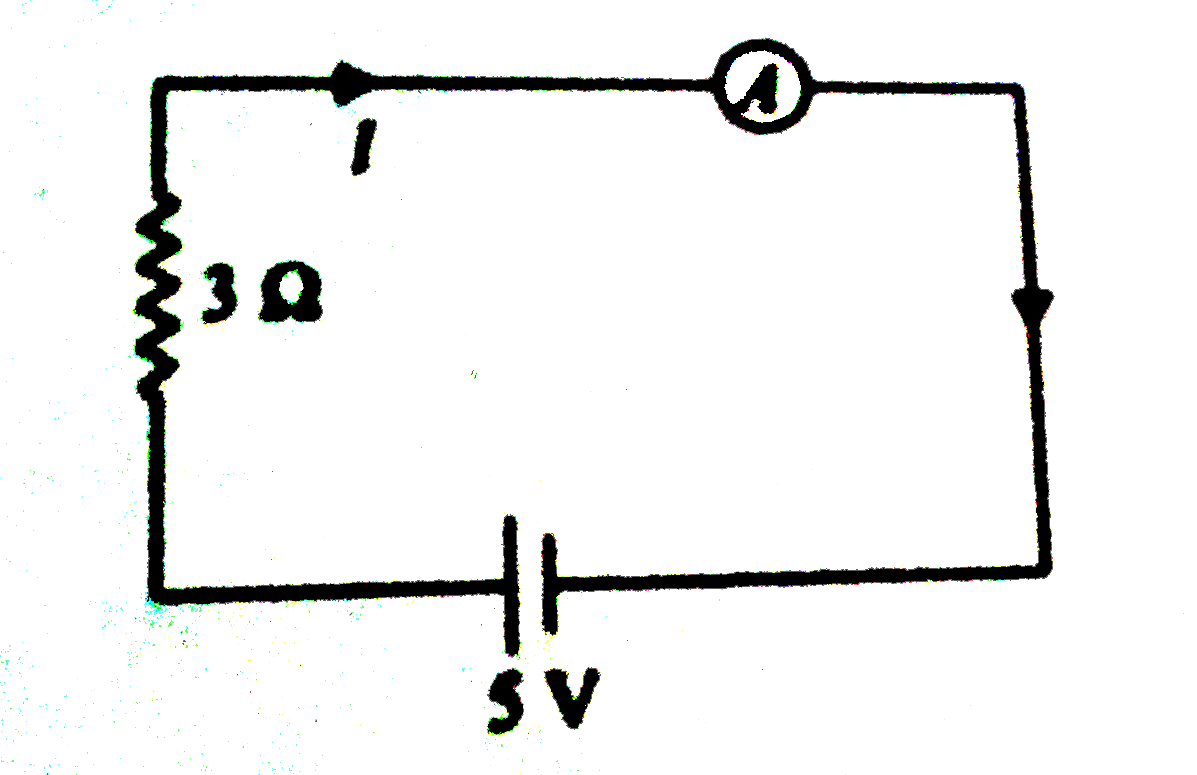 View Solution
View SolutionDeflection of galvanometer in the circuit is 71 divisions. A shunt of 15Ω is connected parallel to galvanometer and value of R is adjusted such that main current ramains the same. If the deflection in the galvanometer falls to 15 divisions then the resistance G of galvanometer in (in ohm)
 View Solution
View SolutionCurrent passing through galvanometer is 0.002A and resistance of galvanometer is Rg=50Ω find out shunt resistance to convert it into ammeter of range 0.5 A
View SolutionThe resistance of a galvanometer is 50 ohm and the maximum current which can be passed through it is 0.002 A. what resistance must be connected to it in order to convert it into an ammeter of range 0-0.5 A ?
View Solution

