In a ammeter 0.2% of main current passes through the galvanometer. If resistance of galvanometer is G, the resistance of ammeter will be
1499G
499500G
1500G
500499G
The correct Answer is:A
To find the resistance of the ammeter when 0.2% of the main current passes through the galvanometer, we can follow these steps:
1. Understanding the Current Distribution:
- Let the total current in the circuit be I.
- According to the problem, 0.2% of the main current passes through the galvanometer.
- Therefore, the current through the galvanometer Ig=0.002I.
- The remaining current that passes through the shunt resistance Is=I−Ig=I−0.002I=0.998I.
2. Applying Ohm's Law:
- The potential drop across the galvanometer and the shunt resistance must be the same when they are connected in parallel.
- The potential drop across the galvanometer can be expressed as:
Vg=Ig×G=0.002I×G
- The potential drop across the shunt resistance can be expressed as:
Vs=Is×S=0.998I×S
3. Setting the Potential Drops Equal:
- Since both potential drops are equal, we can set up the equation:
0.002I×G=0.998I×S
- We can cancel I from both sides (assuming I≠0):
0.002G=0.998S
4. Solving for Shunt Resistance S:
- Rearranging the equation gives:
S=0.002G0.998
- Simplifying this expression:
S≈G499
- This approximation holds because 0.002/0.998 is approximately 1/499.
5. Finding the Total Resistance of the Ammeter:
- The total resistance of the ammeter Ra is the combination of the shunt resistance S and the galvanometer resistance G in parallel:
Ra=G⋅SG+S
- Substituting S:
Ra=G⋅(G499)G+G499
- Simplifying this expression:
Ra=G2/499G(1+1499)=G2/499G⋅500499=G500
Final Result:
The resistance of the ammeter is:
Ra≈G499
- Let the total current in the circuit be I.
- According to the problem, 0.2% of the main current passes through the galvanometer.
- Therefore, the current through the galvanometer Ig=0.002I.
- The remaining current that passes through the shunt resistance Is=I−Ig=I−0.002I=0.998I.
- The potential drop across the galvanometer and the shunt resistance must be the same when they are connected in parallel.
- The potential drop across the galvanometer can be expressed as:
Vg=Ig×G=0.002I×G
- The potential drop across the shunt resistance can be expressed as:
Vs=Is×S=0.998I×S
- Since both potential drops are equal, we can set up the equation:
0.002I×G=0.998I×S
- We can cancel I from both sides (assuming I≠0):
0.002G=0.998S
- Rearranging the equation gives:
S=0.002G0.998
- Simplifying this expression:
S≈G499
- This approximation holds because 0.002/0.998 is approximately 1/499.
- The total resistance of the ammeter Ra is the combination of the shunt resistance S and the galvanometer resistance G in parallel:
Ra=G⋅SG+S
- Substituting S:
Ra=G⋅(G499)G+G499
- Simplifying this expression:
Ra=G2/499G(1+1499)=G2/499G⋅500499=G500
The resistance of the ammeter is:
Ra≈G499
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Match the columns
4 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
If 2% of the main current is to be passed through the galvanometer of resistance G, the resistance of shunt required is
View SolutionIn a galvanometer 5% of the total current in the circuit passes through it. If the resistance of the galvanometer is G, the shunt resistance 'S' connected to the galvanometer is
View SolutionCurrent passing through galvanometer is 0.002A and resistance of galvanometer is Rg=50Ω find out shunt resistance to convert it into ammeter of range 0.5 A
View SolutionTo send 10% of the main current through a moving coil galvanometer of resistance 9 Ω, shunt S required is

View SolutionThe shunt required for 10% of main current to be sent through the moving coil galvanometer of resistance 99Ω will be-
View SolutionTo send 10% of the main current through a moving coil galvanometer of resistance 99Ω, the shunt required is –
View SolutionIf only one hundredth part of total current flowing in the circuit is to be passed through a galvanometer of resistance GΩ, Then the value of shunt resistance required will be-
View SolutionA galvanometer measures current which passes through it. A galanometer can measure typically carrent of order of mA. To be able to measure currents of the order of amperes of main current, a shunt resistance 'S' is connected in parallel with galvanometer.
If resistance of galavonometer is 10Ω and maximum current ig is 10mA then the shunt resistance required so that the main current 'I' can be upto 1A is (in Ω)
View SolutionA moving coil galvnometer is converted into an ammeter reading up to 0.03A by connecting a shunt of resistance r4. What is the maximum current which can be sent through this galvanometer if no shunt is used (here r=resistance of galvanometer)
View SolutionThe reading of the ideal ammeter will be (Resistance of ideal ammeters is zero)
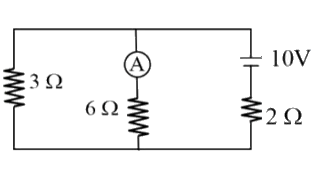
View Solution
