In a horizontal spring-block system force constant of spring is k = 16N/m, mass of the block is 1 kg. Maximum kinetic energy of the block is 8J. Then
amplitude of osciallation is 1m
at half the amplitude, potential energy stored in the spring is 2J.
at half the amplitude kinetic energy is 6J
angular frequency of oscillation is 16 rad/s
The correct Answer is:A, B, C
To solve the problem step by step, we will analyze the given information and apply the principles of simple harmonic motion (SHM).
Step 1: Understand the given data
- Spring constant (k) = 16 N/m
- Mass of the block (m) = 1 kg
- Maximum kinetic energy (KE_max) = 8 J
Step 2: Find the amplitude of oscillation
The maximum kinetic energy in a spring-block system occurs at the mean position and is given by the formula:
KEmax=12kA2
Where A is the amplitude. Rearranging the formula to find A:
A2=2KEmaxk
Substituting the known values:
A2=2×8J16N/m=1616=1
Taking the square root gives:
A=1m
Step 3: Calculate potential energy at half the amplitude
At half the amplitude (A2=12m), the potential energy (PE) stored in the spring is given by:
PE=12kx2
Where x=A2. Substituting the values:
PE=12×16N/m×(12m)2=12×16×14=2J
Step 4: Calculate kinetic energy at half the amplitude
Using the conservation of mechanical energy:
Etotal=KE+PE
At half the amplitude, we know:
Etotal=8JandPE=2J
Thus, the kinetic energy (KE) at half the amplitude is:
KE=Etotal−PE=8J−2J=6J
Step 5: Calculate the angular frequency of oscillation
The angular frequency (ω) can be calculated using the formula:
ω=√km
Substituting the known values:
ω=√16N/m1kg=√16=4rad/s
Summary of Results
1. Amplitude A=1m (Correct)
2. Potential energy at half the amplitude = 2 J (Correct)
3. Kinetic energy at half the amplitude = 6 J (Correct)
4. Angular frequency ω=4rad/s (Incorrect if stated as 16 rad/s)
Final Answer
The correct options are:
1. Amplitude is 1 m (Correct)
2. Potential energy at half the amplitude is 2 J (Correct)
3. Kinetic energy at half the amplitude is 6 J (Correct)
4. Angular frequency is 4 rad/s (Incorrect)
- Spring constant (k) = 16 N/m
- Mass of the block (m) = 1 kg
- Maximum kinetic energy (KE_max) = 8 J
The maximum kinetic energy in a spring-block system occurs at the mean position and is given by the formula:
KEmax=12kA2
Where A is the amplitude. Rearranging the formula to find A:
A2=2KEmaxk
Substituting the known values:
A2=2×8J16N/m=1616=1
Taking the square root gives:
A=1m
At half the amplitude (A2=12m), the potential energy (PE) stored in the spring is given by:
PE=12kx2
Where x=A2. Substituting the values:
PE=12×16N/m×(12m)2=12×16×14=2J
Using the conservation of mechanical energy:
Etotal=KE+PE
At half the amplitude, we know:
Etotal=8JandPE=2J
Thus, the kinetic energy (KE) at half the amplitude is:
KE=Etotal−PE=8J−2J=6J
The angular frequency (ω) can be calculated using the formula:
ω=√km
Substituting the known values:
ω=√16N/m1kg=√16=4rad/s
1. Amplitude A=1m (Correct)
2. Potential energy at half the amplitude = 2 J (Correct)
3. Kinetic energy at half the amplitude = 6 J (Correct)
4. Angular frequency ω=4rad/s (Incorrect if stated as 16 rad/s)
The correct options are:
1. Amplitude is 1 m (Correct)
2. Potential energy at half the amplitude is 2 J (Correct)
3. Kinetic energy at half the amplitude is 6 J (Correct)
4. Angular frequency is 4 rad/s (Incorrect)
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Comprehension types
18 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Matrix matching type questions
13 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - JEE Advanced
34 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
In the two block spring system, force constant of spring is k = 6N/m. Spring is stretched by 12 cm and then left. Match the following.

View SolutionComparing the L-C oscillations with the oscillations of a spring-block system (force constant of spring=k and mass of block=m), the physical quantity mk is similar to
View SolutionTwo blocks A and B are connected to each other by a string and a spring, the string passes over a frictionless pulley as shown in the figure. Block B slides over the horizontal top surface of a stationary block C and the block A slides along the vertical side of C, both with the same uniform speed. The coefficient of friction between the surfaces of blocks is 0.2. Force constant of the spring is 1960 newtons/m. If mass of block A is 2 kg. The mass of block B and the energy stored in the spring are _____ kg and _____ J.

View SolutionThe system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10N/m.
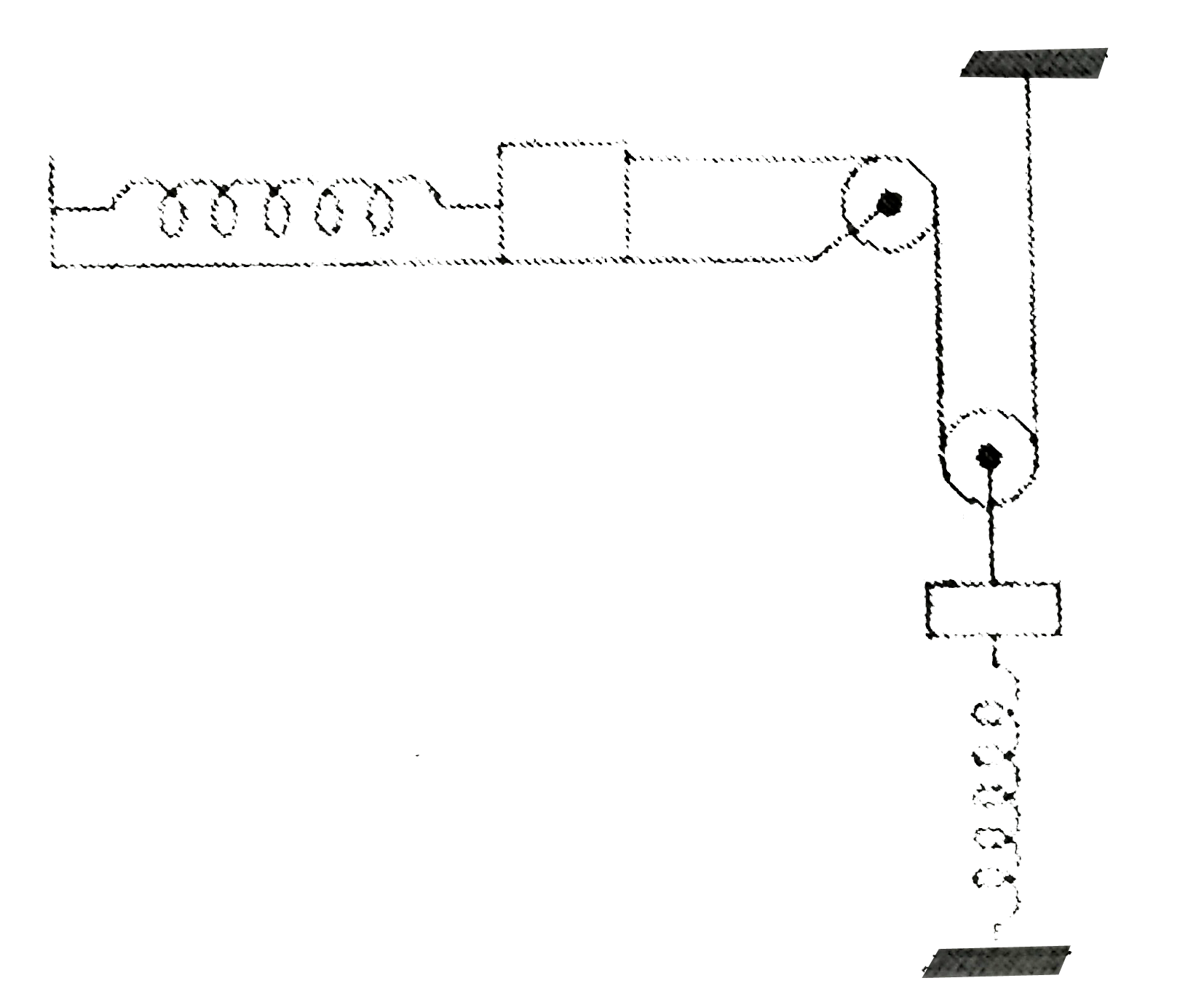
In the equilibrium position, speed of the block placed horizontally is
View SolutionA constant force F is applied on a spring block system as shown in figure. The mass of the block is m and spring constant is k. The block is placed over a smooth surface. Initially the spring was unstretched. Choose the correct alternative(s)

View SolutionA block of mass m is initially moving to the right on a horizontal frictionless surface at a speed v. It then compresses a spring of spring constant k. At the instant when the kinetic energy of the block is equal to the potential energy of the spring, the spring is compressed a distance of :
View SolutionThe blocks ov mass m1=1kg and m2=2kg are connected by an ideal spring, rest on a rough horizontal surface. The spring is unstressed. The spring constant of spring is K=2N/m. The coefficient of friction between blocks and horizontal surface is μ=12. Now the left block is imparted a velocity u towards right as shown. The largest value of u( in m/s) such that the block of mass m2 never moves is ( Take g=10m/s2)
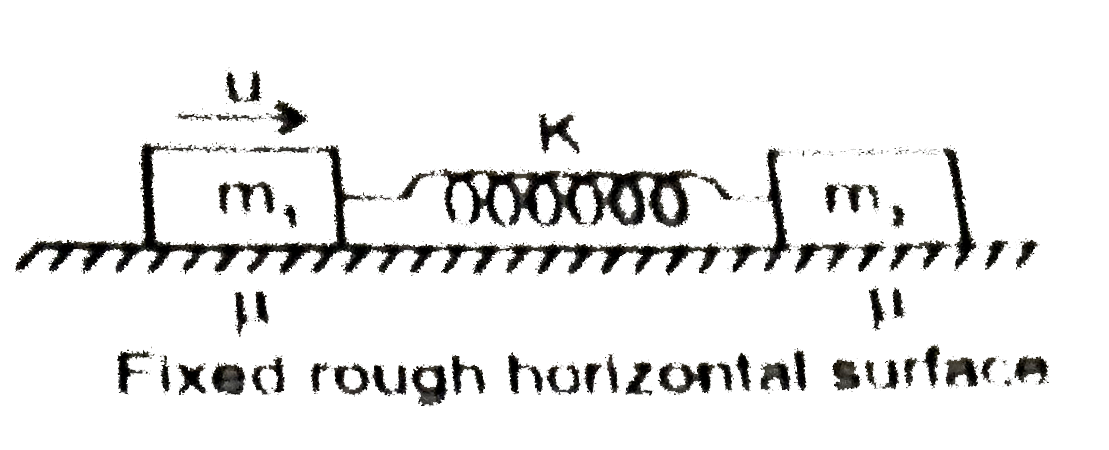
View SolutionA constant force produces maximum velocity V on the block connected to the spring of force constant K as shown in the figure. When the force constant of spring becomes 4K, the maximum velocity of the block is

View SolutionIn the figure shown, all surfaces are smooth and force constant of spring is 10N/m. Block of mass (2 kg) is attaced with the spring. The spring is compressed by (2m) and then released. Find the maximum distance d travelled by the block over the inclined plane. Take g=10m/s2.
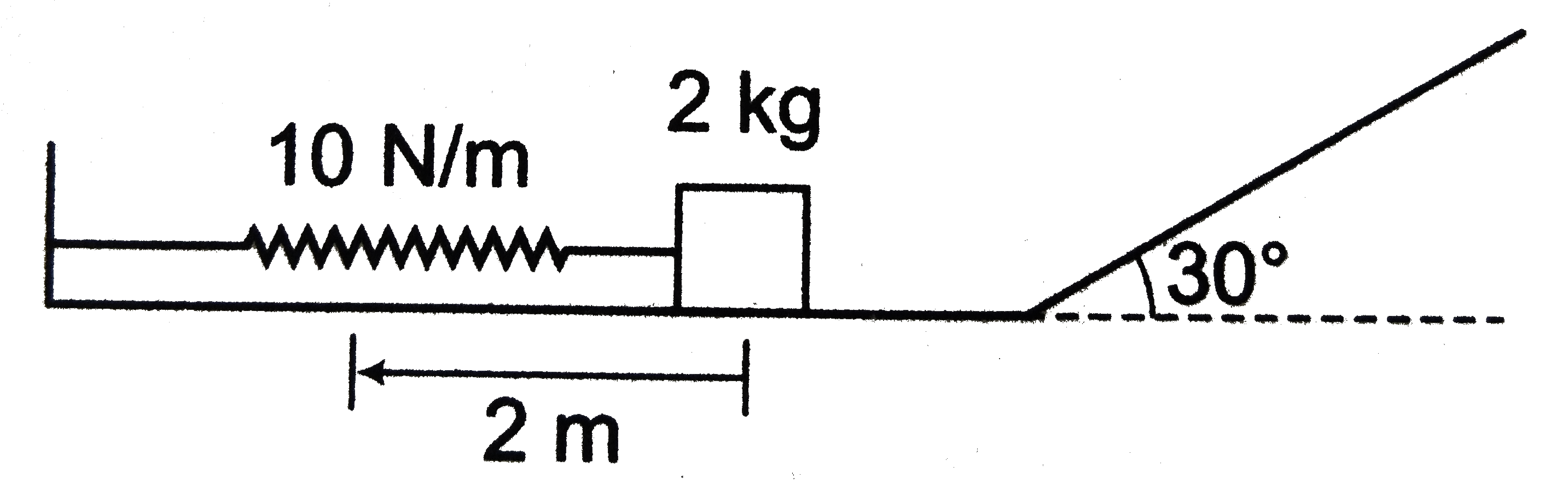 .
.
View SolutionA block of mass M=1 kg resting on a smooth horizontal surface is connected to a horizontal light spring of spring constant k=6N/m whose other end is fixed to a verticall wall. Another block of mass m=0.5 kg is placed over the block M. If the coefficient of friction between the two blocks μ=0.4, find the maximum kinetic energy (in J) that the system can have for simple hormonic oscillation under the action of the spring.
View Solution
