In a simple harmonic oscillator, at the mean position
Kinetic energy is minimum, potential energy is maximum
Both kinetic and potential energies are maximum
Kinetic energy is maximum, potential energy is minimum
Kinetic energy is maximum, potential energy is minimum
The correct Answer is:C
Step by step video, text & image solution for In a simple harmonic oscillator, at the mean position by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESS CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Time period and frequency
18 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESS CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - simple pendulum
61 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESS CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Acceleration of simple Harmonic motion
21 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on motion of connected mass)
10 Videos
- SURFACE TENSIONBOOK - ERRORLESS CHAPTER - SURFACE TENSIONEXERCISE - Exercise
214 Videos
Similar Questions
The figure gives the displacement versus time graph of a simple harmonic oscillator. The position with maximum speed directed down wards is at
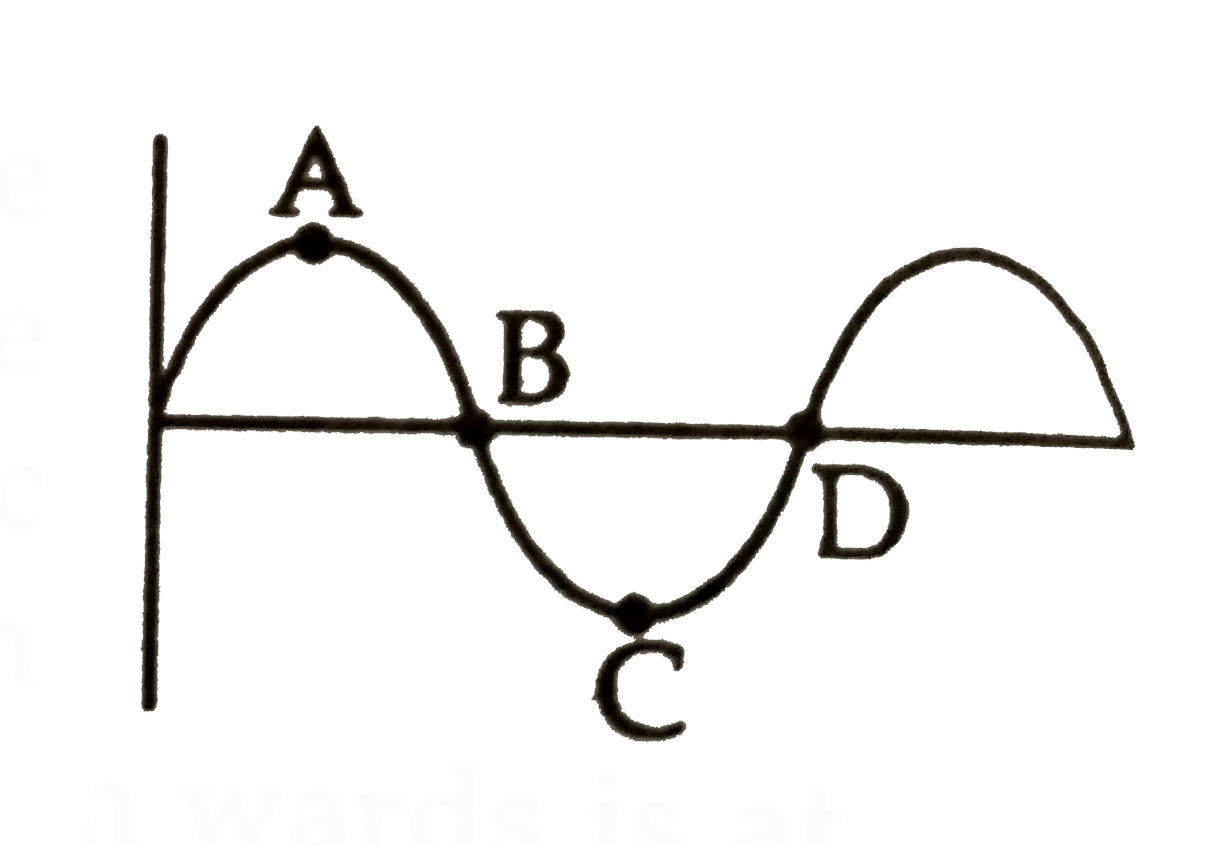
View SolutionIn a simple harmonic oscillation, what fraction of total mechanical energy is in the form of kinetic energy, when the particle is midway between mean and extreme position.
View Solution
Knowledge Check
Velocity of a simple harmonic oscillator in the mean position is v0. If its amplitude is doubled, without changing its period of oscillation, its velocity in the mean position will be
Av0/(2)B2v0Cv0Dv0/4When a longitudinal wave propagates through a medium, the particles of the medium execute simple harmonic oscillations about their mean positions. These oscillations of a particle are characterised by an invariant
AKinetic energyBPotential energyCSum of kinetic energy and potential energyDDifference between kinetic energy and potential energyA simple harmonic oscillator starts from mean position at time, t = 0, moves along +x-direction are reaches the extreme point in 1s covering a distance of 20 cm
(a) The equation of its motion is x=0.2cosπ2t
(b) Its maximum speed is 0.314 ms−1
(c) Its angular frequency is π2rads−1
(d) Its maximum acceleration is π2100ms−2Aa, b, c, d are correctBa, b, c are correctCb, c, d are correctDb, c are correct
Simple harmonic oscillations are
View SolutionIn simple harmonic motion, at the extreme positions
View SolutionThe energy of a simple harmonic oscillator in the state of rest is 3 Joules. If its mean K.E. is 4 joules, its total energy will be :
View SolutionFor a simple harmonic oscillator, the aceeleration is 3m/s2 when the displacement is 0.03 m. The angular frequency of the oscillator is
View SolutionSTATEMENT-1 : In simple harmonic motion, at extreme position the velocity and acceleration of object is zero.
STATEMENT-2 : In simple harmonic motion at mean position?
View Solution
