The energy of a simple harmonic oscillator in the state of rest is 3 Joules. If its mean K.E. is 4 joules, its total energy will be :
7J
8J
10J
11J
The correct Answer is:D
To solve the problem step by step, we can follow these calculations:
Step 1: Understand the given information
- The energy of the simple harmonic oscillator in the state of rest (potential energy at maximum displacement) is given as 3 Joules.
- The mean kinetic energy is given as 4 Joules.
Step 2: Determine the kinetic energy at the mean position
In simple harmonic motion, the total energy (E) is the sum of kinetic energy (KE) and potential energy (PE). At the mean position, the potential energy is zero, and all the energy is kinetic.
The mean kinetic energy is given as 4 Joules. The kinetic energy at the mean position (E2) is twice the mean kinetic energy:
E2=2×Mean K.E.=2×4 Joules=8 Joules
Step 3: Calculate the total energy
The total energy (E) of the simple harmonic oscillator is the sum of the potential energy when at rest (E1) and the kinetic energy at the mean position (E2):
E=E1+E2
Where:
- E1=3 Joules (energy in the state of rest)
- E2=8 Joules (kinetic energy at the mean position)
Now substituting the values:
E=3 Joules+8 Joules=11 Joules
Final Answer
The total energy of the simple harmonic oscillator is 11 Joules.
---
- The energy of the simple harmonic oscillator in the state of rest (potential energy at maximum displacement) is given as 3 Joules.
- The mean kinetic energy is given as 4 Joules.
In simple harmonic motion, the total energy (E) is the sum of kinetic energy (KE) and potential energy (PE). At the mean position, the potential energy is zero, and all the energy is kinetic.
E2=2×Mean K.E.=2×4 Joules=8 Joules
The total energy (E) of the simple harmonic oscillator is the sum of the potential energy when at rest (E1) and the kinetic energy at the mean position (E2):
E=E1+E2
Where:
- E1=3 Joules (energy in the state of rest)
- E2=8 Joules (kinetic energy at the mean position)
E=3 Joules+8 Joules=11 Joules
The total energy of the simple harmonic oscillator is 11 Joules.
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - EXERCISE -3 Section - A Previous Year Problems | NEET24videos
SIMPLE HARMONIC MOTION
- BOOK - MOTIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - EXERCISE -3 Section - B Previous Year Problems | JEE MAIN23videos
SIMPLE HARMONIC MOTION
- BOOK - MOTIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - EXERCISE -1 (Objective Problems | NEET) SECTION-E Simple Pendulum6videos
SIMPLE HARMONIC MOTION
- BOOK - MOTIONCHAPTER - SEMI CONDUCTOR AND LOGIC GATESEXERCISE - EXERCISE 334videos
SEMI CONDUCTOR AND LOGIC GATES
- BOOK - MOTIONCHAPTER - SIMPLE HARONIC MOTION EXERCISE - EXERCISE -4 (Leve-II) [ JEE 2011]11videos
SIMPLE HARONIC MOTION
Similar Questions
When the displacement of a simple harmonic oscillator is half of its amplitude, its potential energy is 3J. Its total energy is
View SolutionThe total energy of a harmonic oscillator of mass 4 kg is 18 Joules. If its energy at rest is 10 Joules then its K. E. at the mean position will be
View Solution
Knowledge Check
- Question 1 - Select One
The average kinetic energy of a simple harmonic oscillator is 2 joule and its total energy is 5 joule. Its minimum potential energy is
A1JB1.5JC2JD3J - Question 2 - Select One
The potential energy of a simple harmonic oscillator of mass 2 kg in its mean position is 5 J. If its total energy is 9 J and its amplitude is 0.01 m, its time period would be
Aπ10sBπ20sCπ50sDπ100s - Question 3 - Select One
Find the average kinetic energy of a simple harmonic oscillator if its total energy is 10 joule and minimum potential energy is 2 joule.
A1JB4JC8JD5J
The variation of potential energy (U) of a simple harmonic oscillator is as shown. Then force constant of the system is (PE is in joules, displacement 'x' is in mm)
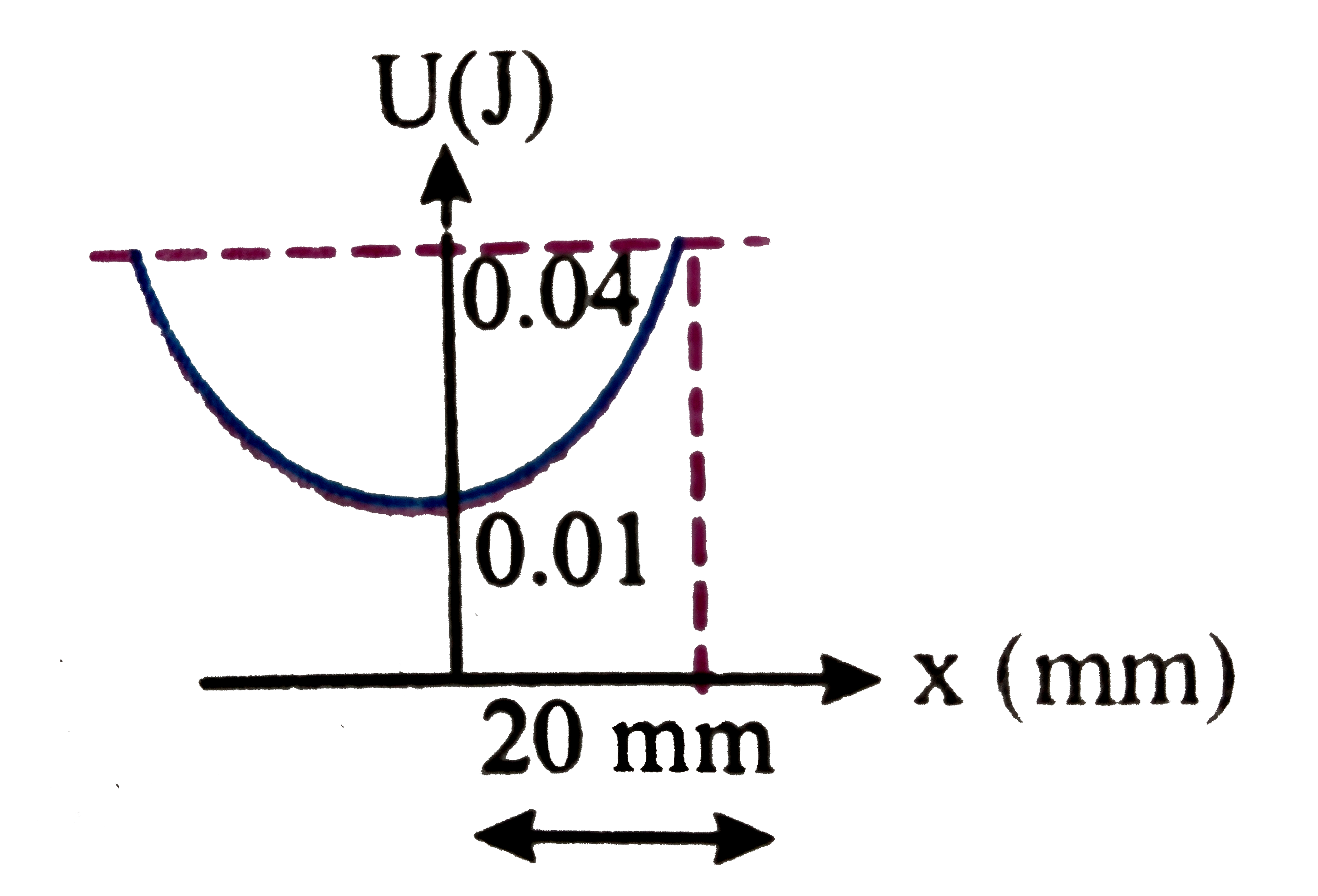 View Solution
View SolutionVelocity of a simple harmonic oscillator in the mean position is v0. If its amplitude is doubled, without changing its period of oscillation, its velocity in the mean position will be
View SolutionThe potential energy of a harmonic oscillator of mass 2kg in its equilibrium position is 5 joules. Its total energy is 9 joules and its amplitude is 1cm. Its time period will be
View SolutionIf the total energy of a simple harmonic oscillator is E, then its potential energy, when it is halfway to its endpoint will be
View SolutionThe PE of a simple harmonic oscillator 0.1 s after crossing the mean position is 1/4 of its total energy. Then the period of its oscillation is
View Solution

