In a single slit diffraction of light of wavelength λ by a slit of width e, the size of the central maximum on a screen at a distance b is
(a) 2bλ+e
(b) 2bλe
(c) 2bλe=e
(d) 2bλe−e
The correct Answer is:C
The direction in which the first minima occurs is θ (say). Then esinθλ or eθ=λ or, θ=λe
(∵θ=sinθ when θ small)
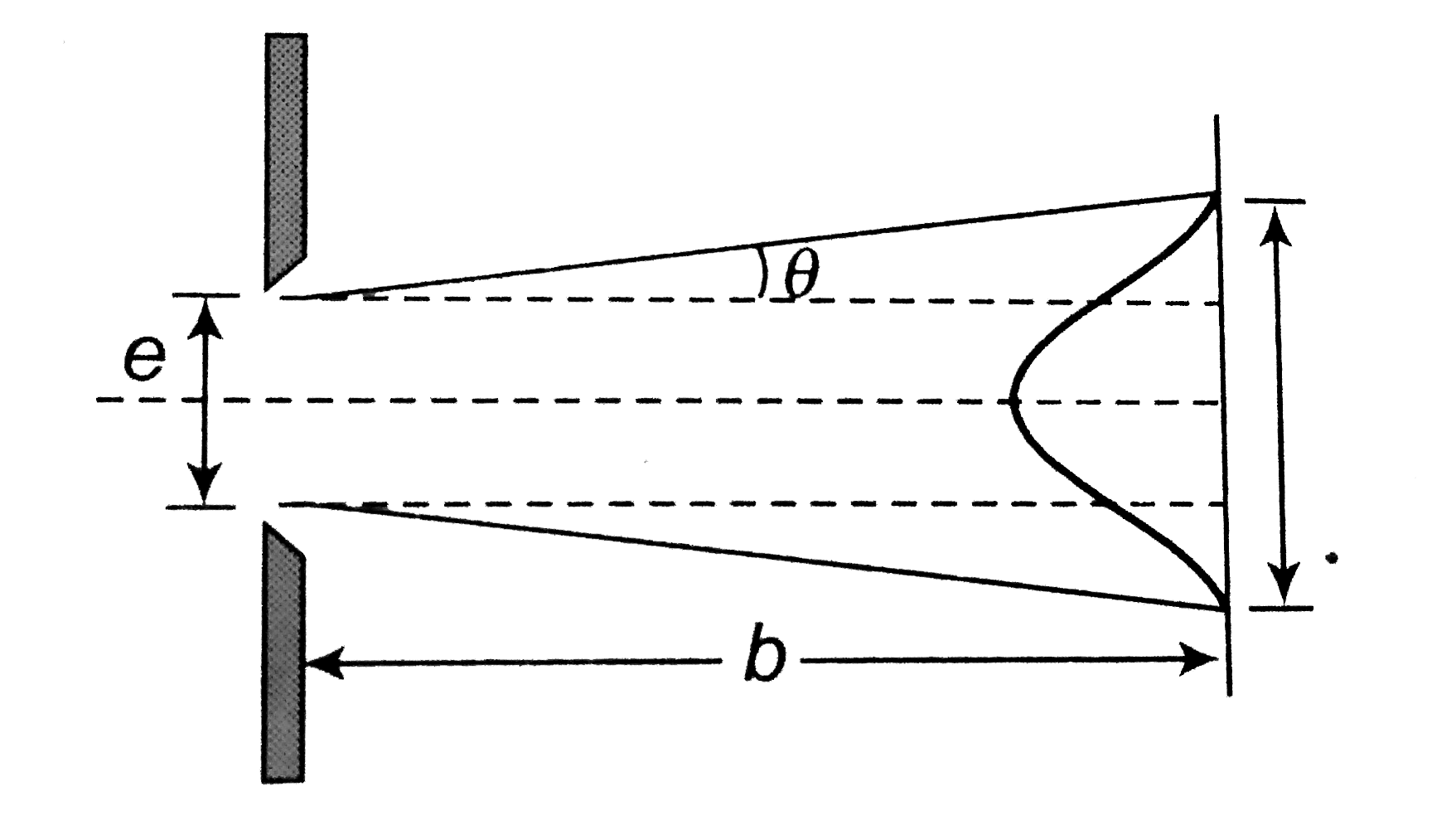
Width of the central maximum =2bθ+e=2b⋅λe+e
Topper's Solved these Questions
- WAVE OPTICSBOOK - A2ZCHAPTER - WAVE OPTICSEXERCISE - Assertion Reason
16 Videos
- WAVE OPTICSBOOK - A2ZCHAPTER - WAVE OPTICSEXERCISE - Section D - Chapter End Test
29 Videos
- WAVE OPTICSBOOK - A2ZCHAPTER - WAVE OPTICSEXERCISE - AIPMT/NEET Questions
22 Videos
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
In a single-slit diffraction experiment, light of wavelength λ illuminates the slit of width 'a' and the diffraction pattern is observed on a screen.
(a) Show the intensity distribution in the pattern with the angular position θ.
(b) How are the intensity and angular width of central maxima affected when
(i) width of slit is increased, and
(ii) separation between slit and screen is decreased ?
View Solution(a) Derive the relation a sinθ=λ for the first minimum of the diffraction pattern produced due to a single slit of width ‘a’ using light of wavelengthλ.
(b) State with reason, how the linear width of central maximum will be affected if
(i) monochromatic yellow light is replaced with red light, and
(ii) distance between the slit and the screen is increased.
(c) Using the monochromatic light of same wavelength in the experimental set-up of the diffraction pattern as well as in the interference pattern where the slit separation is 1 mm, 10 interference fringes are found to be within the central maximum of the diffraction pattern. Determine the width of the single slit, if the screen is kept at the same distance from the slit in the two cases.
View Solution
Knowledge Check
If we observe the single slit Fraunhofer diffraction with wavelength λ and slit width e, the width of the central maxima is θ. On decreasing the slit width for the same λ :
Aθ increasesBθ remains unchangedCθ decreasesDθ increases or decreases depending on the intensity of lightIf we observe the single slit Fraunhofer diffraction with wavelength λ and slit width e, the width of the central maxima is θ. On decreasing the slit width for the same λ :
Aθ increasesBθ remains unchangedCθ decreasesDθ increases or decreases depending on the intensity of lightIf we observe the single slit Fraunhofer diffraction with wavelength λ and slit width e , the width of the central maxima is 2θ . On decreasing the slit width for the same λ
Aθ increasesBθ remains unchangedCθ decreasesDθ increases or decreases depending on the intensity of light
(a) Derive the relation asinθ=λ for the first minimum of the diffraction pattern produced due to a single-slit of width 'a' using light of wavelength λ.
(b) State with reason, how the linear width of central maximum will be affected if (i) monochromatic yellow light is replaced with red light, and (ii) distance between the slit and the screen is increased.
(c) using the monochromatic light of same wavelength in the experimental set-up of the diffraction pattern as well as in the interference pattern where the slit separation is 1mm, 10 interference fringes are found to be within the central maximum of the diffraction pattern. determine the width of the single-slit, if the screen is kept at the same distance from the slit in the two cases.
View SolutionIf we observe the single slit Fraunhofer diffraction with wavelength λ and slit width d, the width of the central maxima is 2θ. On decreasing the slit width for the same λ
View SolutionIn the experiment of diffraction at a single slit, if the slit width is decreased, the wdith of the central maximum
View SolutionIn the experiment of diffraction at a single slit, if the slit width is decreased, the wdith of the central maximum
View SolutionIn a single slit diffraction experiment, the width of the slit is made double its original width. Then the central maximum of the diffraction pattern will become
View Solution
