In a standing wave on a string.
In one time period all the particles are simultaneously at rest twice.
All the particles must be at their positive extremes simultaneously once in one time period
All the particles may be at their positive extremes simultaneously once in a time period.
All the particles are never at rest simultaneously.
The correct Answer is:A, C
Step by step video & image solution for In a standing wave on a string. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Fill in the Blanks Type
34 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Subjective Type
2 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Single Correct Answer Type
56 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - 24
1 Videos
Similar Questions
Statement I : In a standing wave on a string , the spacing between nodes is Δx. If the tension in string is increased wave same as before , then the separation between nearest nodes will be increased.
Statement II : Spacing between nodes ( consecutive) in the standing wave is equal to half of the wavelength of component waves.
View SolutionLet the two waves y1=Asin(kx−ωt) and y2=Asin(kx+ωt) from a standing wave on a string . Now if an additional phase difference of ϕ is created between two waves , then
View SolutionStatement I : In standing waves on a string , the medium particles , i.e., different striung elements remain at rest .
Statement II : In standing waves all the medium particles attain maximum velocity twice in one cycle.
View SolutionAdjacent antinodes of a standing wave on a string are 15.0 cm apart. A particle at an antinode oscillates in simple harmonic motion with amplitude 0.850 cm and period 0.0750 s. The string lies along the +x-axis and is fixed at x=0.
(a) find the displacement of a point on the string as a function of position and time.
(b) Find the speed of propagation of a transverse wave in the string.
(c) Find the amplitude at a point 3.0 cm to the right of an antinode.
View SolutionExplain the formation of standing waves in a string clamped at both ends and discuss the various modes of vibration.
View SolutionThe equation of a standing wave in a string fixed at both its ends is given as y=2A sin kx cos ωt. The amplitude and frequency of a particle vibrating at the point of string midway between a node and an antinode is
View SolutionThe wave-function for a certain standing wave on a string fixed at both ends is y(x,t)=0.5sin(0.025πx)cos500t where x and y are in centimeters and t is seconds. The shortest possible length of the string is :
View SolutionThe vibrations from an 800 Hz tuning fork set up standing waves in a string clamped at both ends. The wave speed in the string is known to be 400m/s for the tension used. The standing wave is observed to have four antinodes. How long is the string?
View SolutionColumn I shows different sets of standing waves in a string of length L whose ends are fixed or free according to respective figure and Column - II shows possible equations for them where symbols have usual meaning
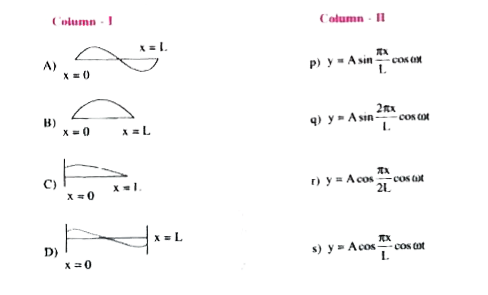
View SolutionA standing wave on a string is given by y=(4cm)cos[xπ]sin[50πt], where x is in metres and t is in seconds. The velocity of the string section at x=1/3matt=1/5s, is
View Solution
