Column I shows different sets of standing waves in a string of length L whose ends are fixed or free according to respective figure and Column - II shows possible equations for them where symbols have usual meaning
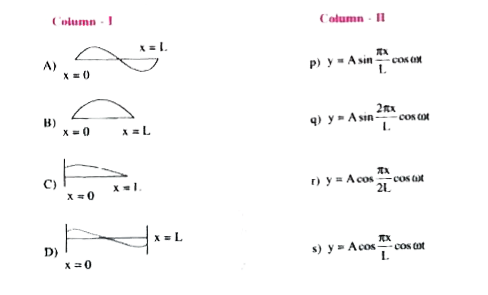
The correct Answer is:A, B, C, D
Step by step video & image solution for Column I shows different sets of standing waves in a string of length L whose ends are fixed or free according to respective figure and Column - II shows possible equations for them where symbols have usual meaning by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - PRACTICE SHEET ADVANCED (INTEGER TYPE QUESTIONS)
10 Videos
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - PRACTICE SHEET ADVANCED (LINKED COMPREHENSION TYPE QUESTIONS)
9 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTSEXERCISE - EXERCISE -3
66 Videos
- WAVE MOTION AND SOUNDBOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - II)
97 Videos
Similar Questions
Draw a diagram to show the shape of a square wave pulse on a string when it gets reflected from (i) fixed boundary and (ii) a free end boundary.
View SolutionColumn-II lists some equations and arrangements of string. They are either corresponding to stationary wave or progressive wave match the entries of column-I with all possible entries in column-II
View SolutionThe wave-function for a certain standing wave on a string fixed at both ends is y(x,t)=0.5sin(0.025πx)cos500t where x and y are in centimeters and t is seconds. The shortest possible length of the string is :
View SolutionFigure shows different standing wave patterns on a string of linear mass density 4.0×10−2kg/m under a tension of 100 N. The amplitude of antinodes is indicated in each figure. The length of the string is 2.0m.
(i) Obtain the frequencies of the modes shown in figures (a) and (b).
(ii)Write down the transverse displacement y as a function of x and t for each mode. (Take the initial configuration of the wire in each mode to be as shown by the dark lines in the figure).

View SolutionString I and II have identical and linear mass densities, but string I is under greater tension than string II. The accompanying figure shows four different situations, A to D, in which standing wave patterns exist on the two strings. In which situation it is possible that strings I and II are oscillating at the same resonant frequency ?
View SolutionA string fixed at both ends has consecutive standing wave modes for which the distances between adjacent nodes are 18 cmand16 cm respectively. The minimum possible length of the string is:
View SolutionFour pieces of string of length L are joined end to end to make a long string of length 4L. The linear mass density of the strings are μ,4μ,9μand16μ, respectively. One end of the combined string is tied to a fixed support and a transverse wave has been generated at the other end having frequency f (ignore any reflection and absorption). string has been stretched under a tension F. Find the time taken by wave to reach from source end to fixed end.

View SolutionA string fixed at both ends has consecutive standing wave modes for which the distances between adjacent nodes are 18 cm and 16 cm, respectively.
(a) What is the minimum possible length of the string?
(b) If the tension is 10 N and the linear mass density is 4 g/m, what is the fundamental frequency?
View SolutionA stationary wave of amplitude A is generated between the two fixed ends x = 0 and x = L. The particle at x=L3 is a node. There are only two particle between x=L6andx=L3 which have maximum speed half of the maximum speed of the anti-node. Again there are only two particles between x= 0 and x=L6 which have maximum speed half of that at the antibodes. The slope of the wave function at x=L3 changes with respect to time according to the graph shown. The symbols μ,ωandA are having their usual meanings if used in calculations.
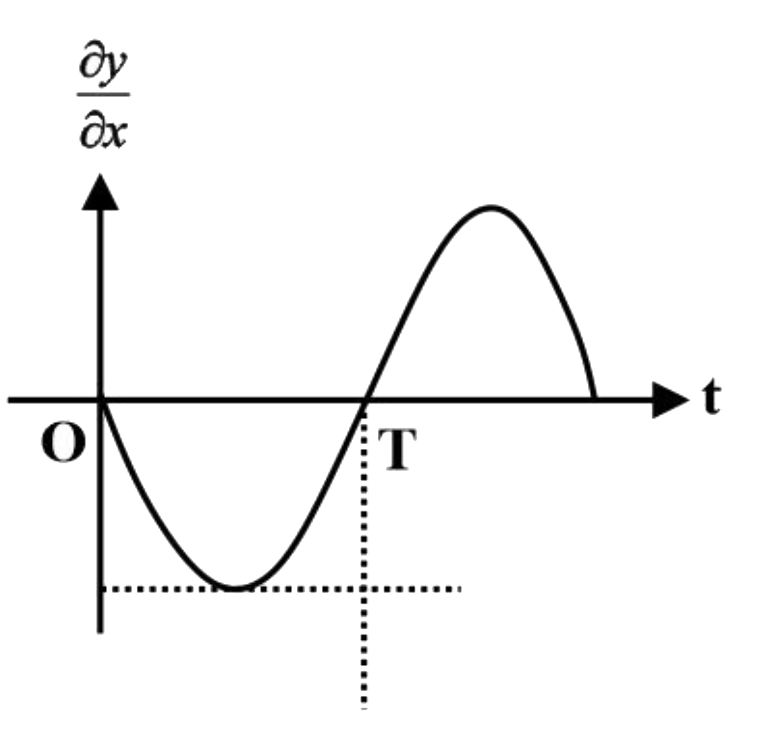
The time period of oscillations of a particle is
View SolutionA light string is tied at one end to a fixed support and to a heavy string of equal length L at the other end as shown in figure. A block of mass m is tied to the free end of heavy string. Mass per unit length of the strings are μ and 9μ and the tension is T. Find the possible values of frequencies such that junction of two wire point A is a node.

View Solution
