In a system of particles 8kg mass is subjected to a force of 16N along + ve x-axis and another 8kg mass is subjected to a force of 8N along + ve y-axis. The magnitude of acceleration of centre of mass and the angle made by it with x-axis are given, respectively, by
√52ms2,θ=45∘
3√5ms2,θ=tan−1(23)
√52ms2,θ=tan−1(12)
1ms2,θ=tan−1√3
The correct Answer is:C
To solve the problem, we need to determine the acceleration of the center of mass of the system of particles and the angle it makes with the x-axis. Here’s the step-by-step solution:
Step 1: Identify the Forces and Masses
We have two masses:
- Mass m1=8kg subjected to a force F1=16N along the positive x-axis.
- Mass m2=8kg subjected to a force F2=8N along the positive y-axis.
Step 2: Calculate the Acceleration of Each Mass
Using Newton's second law F=ma, we can find the acceleration for each mass.
For mass m1:
a1=F1m1=16N8kg=2m/s2(along x-axis)
For mass m2:
a2=F2m2=8N8kg=1m/s2(along y-axis)
Step 3: Calculate the Total Mass of the System
The total mass M of the system is:
M=m1+m2=8kg+8kg=16kg
Step 4: Calculate the Acceleration of the Center of Mass
The acceleration of the center of mass acm can be calculated using the formula:
acm=m1a1+m2a2M
Substituting the values:
acm=8⋅2+8⋅116=16+816=2416=32m/s2
Step 5: Calculate the Components of the Acceleration
The x-component of the acceleration is:
acm,x=m1a1M=8⋅216=1m/s2
The y-component of the acceleration is:
acm,y=m2a2M=8⋅116=0.5m/s2
Step 6: Calculate the Magnitude of the Acceleration of the Center of Mass
Using the Pythagorean theorem:
|acm|=√(acm,x)2+(acm,y)2=√(1)2+(0.5)2=√1+0.25=√1.25=√52m/s2
Step 7: Calculate the Angle Made with the x-axis
The angle θ can be calculated using the tangent function:
tanθ=acm,yacm,x=0.51=0.5
Thus,
θ=tan−1(0.5)
Final Answer
The magnitude of the acceleration of the center of mass is √52m/s2 and the angle made with the x-axis is tan−1(0.5).
We have two masses:
- Mass m1=8kg subjected to a force F1=16N along the positive x-axis.
- Mass m2=8kg subjected to a force F2=8N along the positive y-axis.
Using Newton's second law F=ma, we can find the acceleration for each mass.
a1=F1m1=16N8kg=2m/s2(along x-axis)
a2=F2m2=8N8kg=1m/s2(along y-axis)
The total mass M of the system is:
M=m1+m2=8kg+8kg=16kg
The acceleration of the center of mass acm can be calculated using the formula:
acm=m1a1+m2a2M
Substituting the values:
acm=8⋅2+8⋅116=16+816=2416=32m/s2
The x-component of the acceleration is:
acm,x=m1a1M=8⋅216=1m/s2
acm,y=m2a2M=8⋅116=0.5m/s2
Using the Pythagorean theorem:
|acm|=√(acm,x)2+(acm,y)2=√(1)2+(0.5)2=√1+0.25=√1.25=√52m/s2
The angle θ can be calculated using the tangent function:
tanθ=acm,yacm,x=0.51=0.5
Thus,
θ=tan−1(0.5)
The magnitude of the acceleration of the center of mass is √52m/s2 and the angle made with the x-axis is tan−1(0.5).
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct
25 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Subjective
23 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
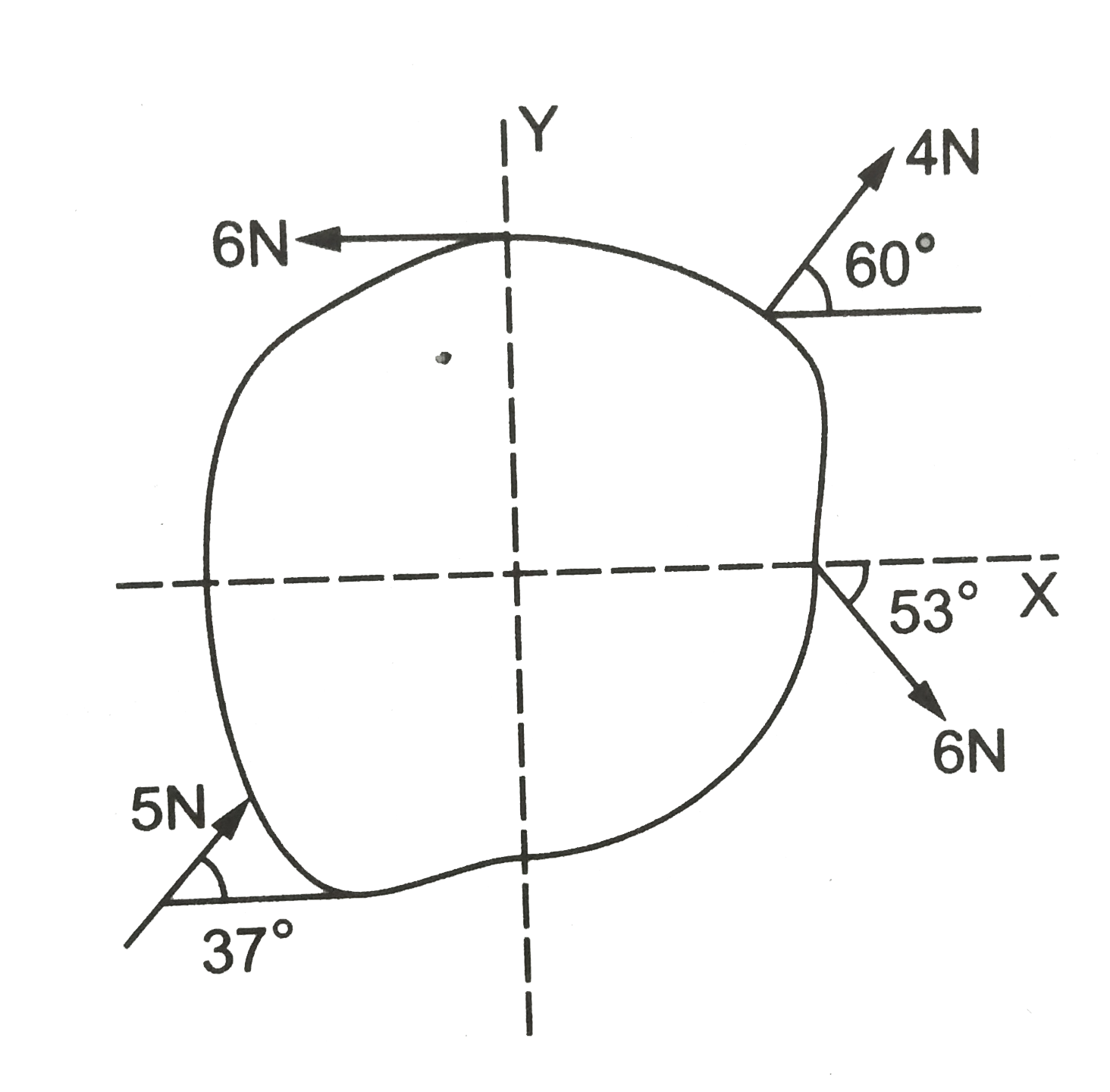
A body of mass 2.5 kg is subjected to the forces shown in figure. Find the acceleration of the centre of maas.
View SolutionA body of mass 10 kg is acted upon by two perpendicular forces , 6 N and 8 N . The resultant acceleration of the body is
View SolutionA body of mass 5 kg is acted upon by two perpendicular forces 8 N and 6 N Give the magnitude and direction of the acceleration of the body.
View SolutionResolve a force F = 10N along x and y-axes. Where this force vector in making an angle of 60∘ from negative x-axis towards nagetive y-axis?
View SolutionThree bodies having masses 5 kg, 4 kg and 2 kg is moving at the speed of 5 m/sand2m//s and 5 m/s respectively along X-axis.The magnitude of velocity of centre of mass is
View SolutionA particle is subjected simultaneously to two SHMs, one along the x - axis and the other along the y - axis. The two vibrations are in phase and have unequal amplitudes. The particle will execute
View SolutionConsider a block of mass 10kg. which rests on as smooth surface and is subjected to a horizontal force of 6N. If observer A is in a fixed frame x.
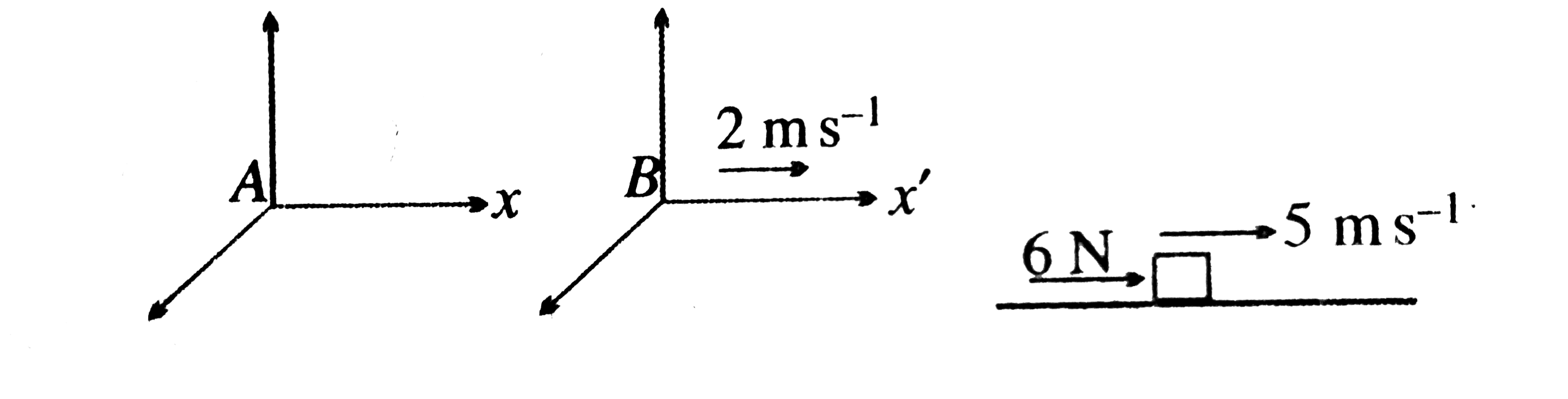
View SolutionA point object of mass m is kept at (a, 0) along x-axis. What mass should be kept at (-3a,0), so that centre of mass lies at origin ?
View SolutionA particle of mass 0.3 kg subject to a force F=−kx with k=15N/m. What will be its initial acceleration if it is released from a point 20cm away from the origin?
View SolutionThree particles of masses 8 kg, 4 kg and 4 kg situated at (4,1), (-2,2) and (1,-3) are acted upon by external forces 6¯jN,−6¯iN and 14¯iN. The acceleration of centre of mass of the system is
View Solution
