In a two diamensional motion of a particle, the particle moves from point A, with position vector →r1 to point B, with position vector →r2. If the magnitudes of these vectors are, respectively, r1=3 and r2=4 and the angles they make with the x-axis are θ1=75∘ and θ2=15∘, respectively, then find the magnitude of the displacement vector.

15
√13
17
√15
The correct Answer is:B
Displacement =−−→AB, angle between →r1 and →r2 is θ=75∘−15∘=60∘
From (Figure), AB2=r21+r22−2r1r2cosθ
=32+42−2×3×4cos60∘=13
⇒AB=√13
Topper's Solved these Questions
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Subjective
28 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Integer
9 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (integer)
4 Videos
Similar Questions
A particle moves from position A to position B in a path as shown in If the poit vectors →r1 and →r2 making an angle θ between them are give, find the magnitude of displacement.
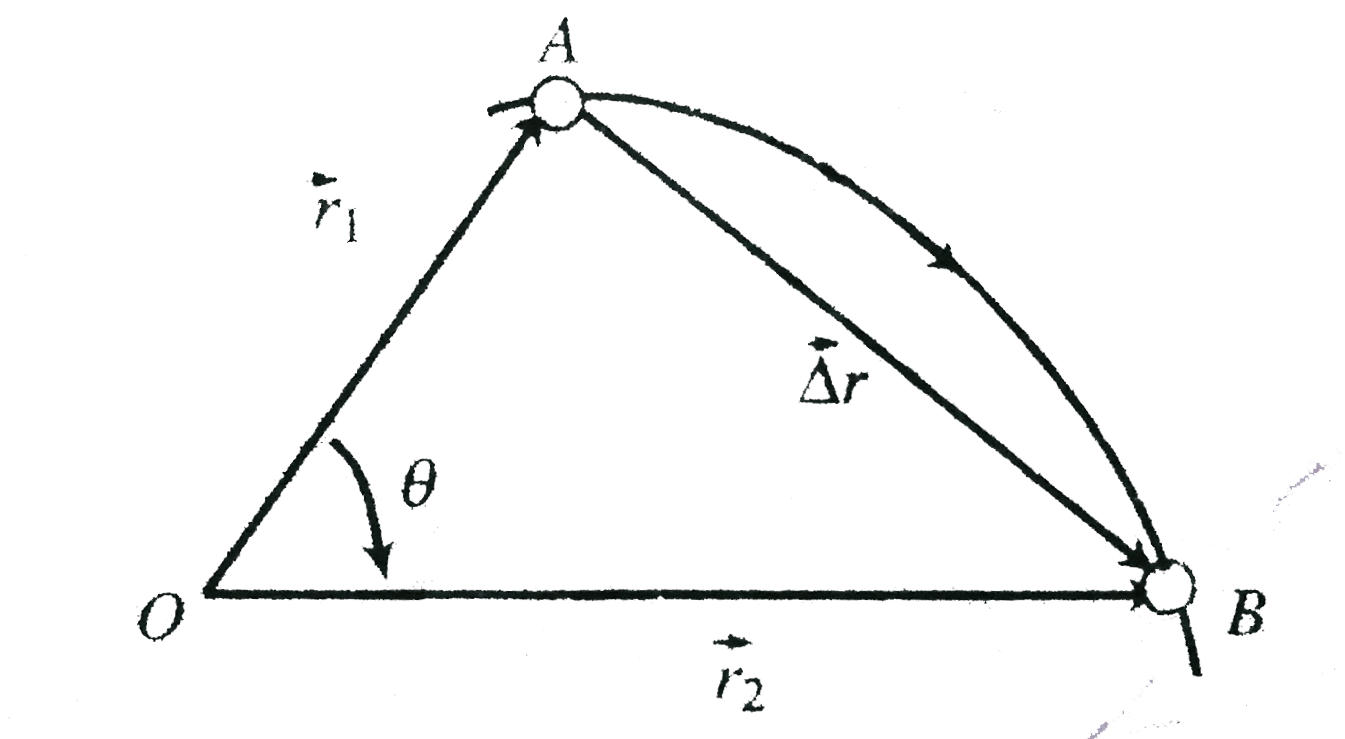 .
.
View SolutionPosition vector of centre of two particles of masses m1 and m2 whose position vectors r1 and r2 then rcm?
View Solution
Knowledge Check
In a two diamensional motion of a particle, the particle moves from point A, with position vector →r1 to point B, with position vector →r2. If the magnitudes of these vectors are, respectively, r1=3 and r2=4 and the angles they make with the x-axis are θ1=75∘ and θ2=15∘, respectively, then find the magnitude of the displacement vector.
 A15B√13C17D√15
A15B√13C17D√15In a two-dimensional motion of a particle, the particle moves from point A of position vector →r1, to point B of vectors are , respectively, r1=3andr2=4 and the angles they make with the x axis are θ1=75∘andθ2=15∘, respectively, then find the magnitude of the displacement vector.
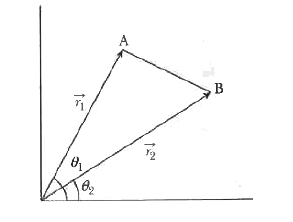 A15B√13C17D√15
A15B√13C17D√15The displacement of a particle from a point having position vector 2ˆi+4ˆj to another point having position vector 5ˆj+1ˆj is
A3 unitsB3√2 unitsC5 unitsD5√3units
Find the position vector of the point, which divides the join of points with position vectors 3→a−2→b and 2→a+3→b in the ratio 2 : 1.
View SolutionFind the position vector of a point R which divides the line joining the two points P and Q with position vectors −−→OP=2→a+→b and −−→OQ=→a−2→b, respectively in the ratio 1:2 internally and externally.
View SolutionA vector →r is inclined at equal angle to the three axes. If the magnitude of →r is 2√3, find →r.
View SolutionFind the position vector of a point which divides the join of points with position vectors →a−2→b and 2→a+→b externally in the ration 2:1.
View SolutionA vector a makes 30∘ and b makes 120∘ angle with the x-axis. The magnitude of these vectors are 3 unit and 4 unit, respectively. The magnitude of resultant vector is
View Solution
