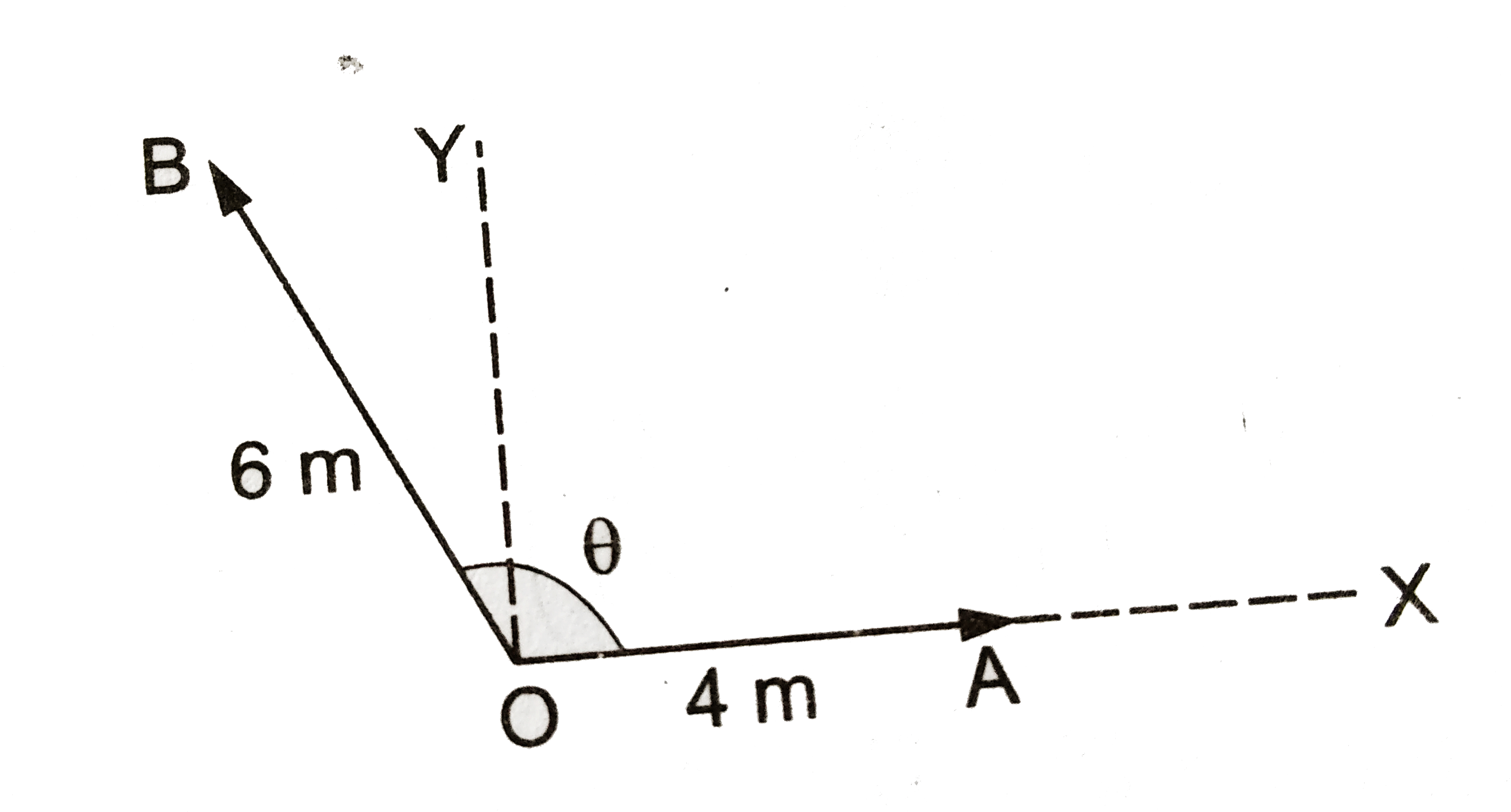
Find the resultant of the three vectors −−→OA,−−→OB and −−→OC shown in figure. Radius of the circle is R.

r
2r
r(1+√2)
r(√2)
The correct Answer is:C
−−→OC and −−→OA are equal in magnitude and inclined to each other at an angle of 90∘, So their resultant is √2r. It acts mid-way between −−→OC and −−→OA,i.e., along OB.
Now, both r and √2r are along the same line and in the same direction.
Resultant =r+√2r=r(1+√2)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
- BOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Subjective28videos
VECTORS
- BOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Integer9videos
TRAVELLING WAVES
- BOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (integer)4videos
WORK, POWER & ENERGY
Similar Questions
Knowledge Check
- Question 1 - Select One
The resultant of the three vectors −−→OA,−−→OB and −−→OC shown in figure is
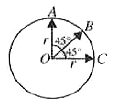 ArB2rCr(1+√s)Dr(√2−1)
ArB2rCr(1+√s)Dr(√2−1) - Question 2 - Select One
What is the angle between the vector →A and →B as shown in figure ?
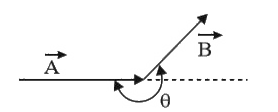 AθBπ−θCθ−πD2π−θ
AθBπ−θCθ−πD2π−θ - Question 3 - Select One
The resultant of two vectors →A and →B is perpendicular to the vector →A and its magnitudes is equal to half of the magnitudes of vector →B (figure). The angle between →A and →B is
 A120∘B150∘C135∘DNone of these
A120∘B150∘C135∘DNone of these
The magnitude of vectors −−→OA,−−→OBand−−→OC in figure are equal. Find the direction of −−→OA+−−→OB−−−→OC.
 .View Solution
.View SolutionThe resultant of two velocity vectors →A and →B is perpendicular to →A. Magnitude of Resultant →R is equal to half magnitude of →B. If the angle between →A and →B is (30θ)∘, then value of θ is ?
View SolutionThe magnitudes of vectors −−→OA,−−→OB and −−→OC in figure(2-W3) are equal. Find the direction of −−→OA+−−→OB−−−→OC.
View SolutionThe sum of the three vectors shown in figure is zero. Find the magnitudes of the vectors −−→OBand−−→OC.
View SolutionABCD is a quadrilateral and E is the point of intersection of the lines joining the middle points of opposite side. Show that the resultant of −−→OA , −−→OB , −−→OC and −−→OD = 4 −−→OE , where O is any point.
View Solution