In a Young's double slit experiment using red and blue lights of wavelengths 600 nm and 480 nm respectively, the value of n for which the nth red fringe coincides with (n+1) th blue fringe is
5
4
3
2
The correct Answer is:A
To solve the problem, we need to find the value of n for which the nth red fringe coincides with the (n+1)th blue fringe in a Young's double slit experiment.
Step 1: Understand the fringe width formula
The fringe width (β) in a Young's double slit experiment is given by the formula:
β=λDd
where:
- λ is the wavelength of light,
- D is the distance from the slits to the screen,
- d is the distance between the slits.
Step 2: Write the equations for red and blue light
For red light with wavelength λR=600nm:
βR=nλR
For blue light with wavelength λB=480nm:
βB=(n+1)λB
Step 3: Set the fringe widths equal
Since the nth red fringe coincides with the (n+1)th blue fringe, we can equate the two fringe width equations:
nλR=(n+1)λB
Step 4: Substitute the wavelengths
Substituting the values of λR and λB:
n×600nm=(n+1)×480nm
Step 5: Simplify the equation
We can cancel out the units of nm:
600n=480(n+1)
Step 6: Expand and rearrange the equation
Expanding the right side:
600n=480n+480
Now, rearranging gives:
600n−480n=480
120n=480
Step 7: Solve for n
Dividing both sides by 120:
n=480120=4
Conclusion
The value of n for which the nth red fringe coincides with the (n+1)th blue fringe is:
4
The fringe width (β) in a Young's double slit experiment is given by the formula:
β=λDd
where:
- λ is the wavelength of light,
- D is the distance from the slits to the screen,
- d is the distance between the slits.
For red light with wavelength λR=600nm:
βR=nλR
For blue light with wavelength λB=480nm:
βB=(n+1)λB
Since the nth red fringe coincides with the (n+1)th blue fringe, we can equate the two fringe width equations:
nλR=(n+1)λB
Substituting the values of λR and λB:
n×600nm=(n+1)×480nm
We can cancel out the units of nm:
600n=480(n+1)
Expanding the right side:
600n=480n+480
Now, rearranging gives:
600n−480n=480
120n=480
Dividing both sides by 120:
n=480120=4
The value of n for which the nth red fringe coincides with the (n+1)th blue fringe is:
4
Topper's Solved these Questions
- WAVE OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion reason
8 Videos
- WAVE OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - WAVE OPTICSEXERCISE - match column
4 Videos
- WAVE OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Check point
65 Videos
- SOLVED PAPERS 2018BOOK - DC PANDEY ENGLISHCHAPTER - SOLVED PAPERS 2018EXERCISE - JIPMER
22 Videos
Similar Questions
In Young's double slit experiment, the wavelength of red light is 7800Å. The value of n for which nth bright band due to red light coincides with (n+1)th bright band due to blue light(λ=5200Angstrom), is
View SolutionThe Young's double slit experiment is performed with blue light and green light of wavelength 4360Å and 5460Å respectively. If y is the distance of 4th maxima from the central one, then
View Solution
Knowledge Check
In Young's double slit experiment, the fringe width with light of wavelength 6000 Ã… is 3 mm. The fringe width, when the wavelength of light is changed to 4000 Ã… is
A3 mmB1 mmC2 mmD4 mm
In Young.s double slit experiment sodium light is replaced by blue lamp, then the fringe width
View SolutionIn Young's double slit experiment, when light of wavelength 4000A∘ is used 90 fringes are seen on the screen. When light of 3000 A is used, the number of fringes seen is
View SolutionIn the Young’s double slit experiment, for which colour the fringe width is least
View SolutionIn a standard Young's double-slit experiment with coherent light of wavelength 600 nm, the fringe width of the fringes in the central region (near the central fringe, P0) is observed it to be 3 mm. An extremely thin glass plate is introduced to be displaced by 11 mm. Another thin plate is placed before the second slit and it is observed that the fringe are now displaced by an additional 12 mm. If the additional optical path lengths introduced are Δ1 and Δ2 then
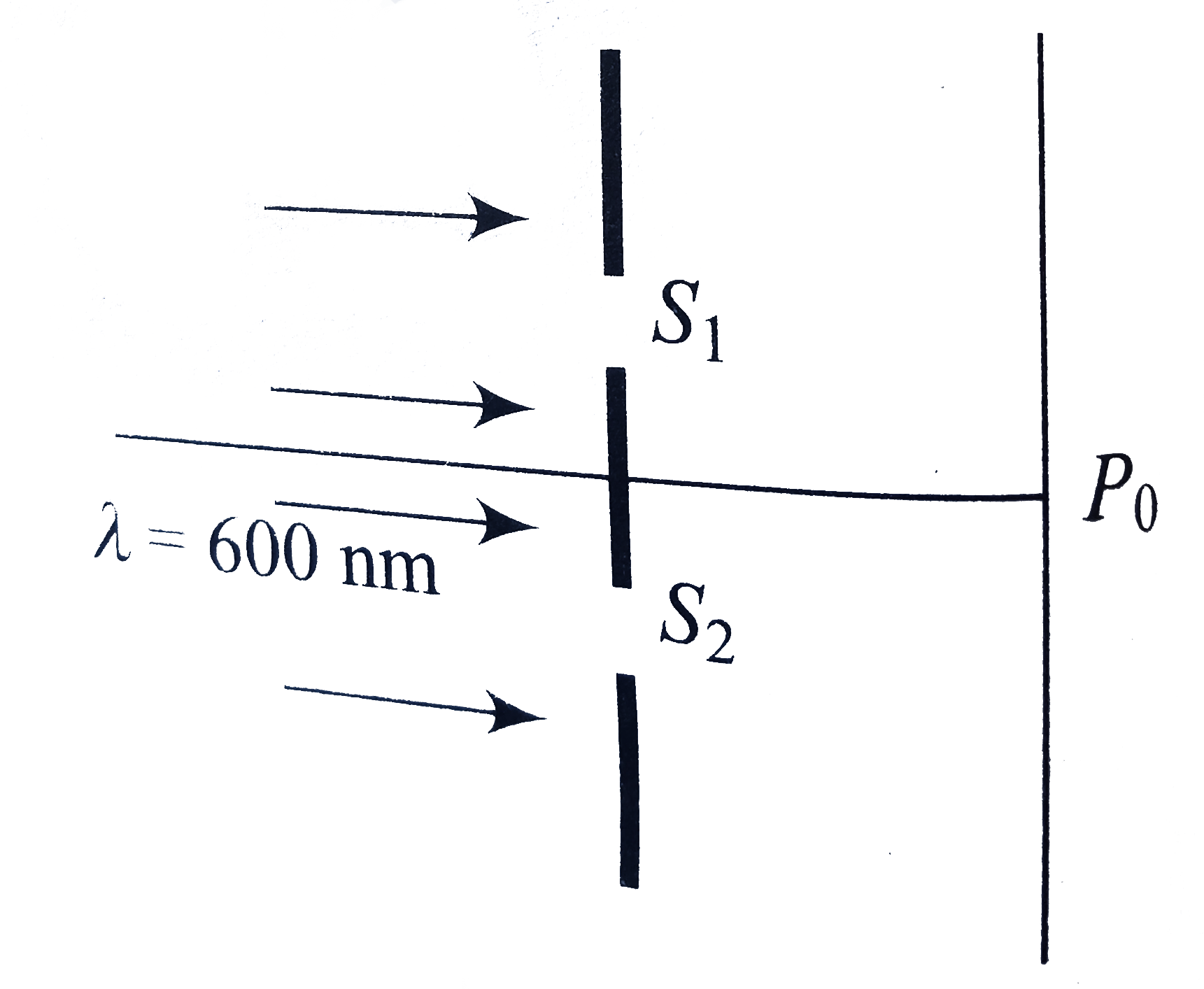
View SolutionIn Young.s double slit experiment using monochromatic light of wavelength 600 nm, 5th bright fringe is at a distance of 0.48 mm from the centre of the pattern. If the screen is at a distance of 80 cm from the plane of the two slits, calculate :
Fringe width, i.e., fringe separation.
View SolutionIn Young's double-slit experiment, if yellow light is replaced by blue light, the interference fringes become
View SolutionIn Young.s double slit experiment using monochromatic light of wavelength 600 nm, 5th bright fringe is at a distance of 0.48 mm from the centre of the pattern. If the screen is at a distance of 80 cm from the plane of the two slits, calculate :
Distance between the two slits.
View Solution
