In the Young's double slit experiment, the intensities at two points P1 and P2 on the screen are respectively I1 and I2 If P1 is located at the centre of a bright fringe and P2 is located at a distance equal to a quarter of fringe width from P1 then I1I2 is
a.2 b.3 c.4 d.None of these
2
3
4
None of these
The correct Answer is:A
To solve the problem, we will follow these steps:
Step 1: Identify the positions of points P1 and P2
- Point P1 is located at the center of a bright fringe, which corresponds to a position where the path difference is zero.
- Point P2 is located at a distance equal to a quarter of the fringe width (β) from P1.
Step 2: Define the fringe width (β)
- The fringe width (β) in the Young's double slit experiment is given by the formula:
β=λDd
where:
- λ is the wavelength of light,
- D is the distance from the slits to the screen,
- d is the distance between the slits.
Step 3: Calculate the position of P2
- Since P2 is at a distance of β4 from P1, we can express this as:
yP2=β4=λD4d
Step 4: Calculate the path difference (Δx)
- The path difference (Δx) for point P2 can be calculated as:
Δx=yP2⋅dD=(λD4d)⋅dD=λ4
Step 5: Calculate the phase difference (Δφ)
- The phase difference (Δφ) corresponding to the path difference can be calculated using the formula:
Δϕ=2πλΔx
Substituting Δx:
Δϕ=2πλ⋅λ4=π2
Step 6: Calculate the intensities (I1 and I2)
- The intensity at point P1 (I1) is at the center of a bright fringe, so:
I1=I0
where I0 is the maximum intensity.
- The intensity at point P2 (I2) can be calculated using:
I2=I0cos2(Δϕ2)
Substituting Δφ:
I2=I0cos2(π4)=I0(1√2)2=I02
Step 7: Calculate the ratio of intensities (I1/I2)
- Now we can find the ratio:
I1I2=I0I02=2
Final Answer
Thus, the ratio I1I2 is:
I1I2=2
- Point P1 is located at the center of a bright fringe, which corresponds to a position where the path difference is zero.
- Point P2 is located at a distance equal to a quarter of the fringe width (β) from P1.
- The fringe width (β) in the Young's double slit experiment is given by the formula:
β=λDd
where:
- λ is the wavelength of light,
- D is the distance from the slits to the screen,
- d is the distance between the slits.
- Since P2 is at a distance of β4 from P1, we can express this as:
yP2=β4=λD4d
- The path difference (Δx) for point P2 can be calculated as:
Δx=yP2⋅dD=(λD4d)⋅dD=λ4
- The phase difference (Δφ) corresponding to the path difference can be calculated using the formula:
Δϕ=2πλΔx
Substituting Δx:
Δϕ=2πλ⋅λ4=π2
- The intensity at point P1 (I1) is at the center of a bright fringe, so:
I1=I0
where I0 is the maximum intensity.
- The intensity at point P2 (I2) can be calculated using:
I2=I0cos2(Δϕ2)
Substituting Δφ:
I2=I0cos2(π4)=I0(1√2)2=I02
- Now we can find the ratio:
I1I2=I0I02=2
Thus, the ratio I1I2 is:
I1I2=2
Topper's Solved these Questions
- WAVE OPTICSBook:DC PANDEY ENGLISHChapter:WAVE OPTICSExercise:Assertion reason
Explore 8 Videos
- WAVE OPTICSBook:DC PANDEY ENGLISHChapter:WAVE OPTICSExercise:match column
Explore 4 Videos
- WAVE OPTICSBook:DC PANDEY ENGLISHChapter:WAVE OPTICSExercise:Check point
Explore 65 Videos
- SOLVED PAPERS 2018Book:DC PANDEY ENGLISHChapter:SOLVED PAPERS 2018Exercise:JIPMER
Explore 22 Videos
Similar Questions
In a Young's double slit experiment, I0 is the intensity at the central maximum and β is the fringe width. The intensity at a point P distant x from the centre will be
View SolutionIn a Young's double slit experiment, I0 is the intensity at the central maximum and β is the fringe width. The intensity at a point P distant x from the centre will be
View Solution
Knowledge Check
In a Young's double slit experiment, let S1 and S2 be the two slits, and C be the centre of the screen. If ∠S1CS2=θ and λ is the wavelength, the fringe width will be
AλθBλθC2λθDλ2θIn Young's double slit experiment, the slits are horizontal. The intensity at a point P as shown in figure is 34I0,whereI0 is the maximum intensity.
Then the value of θ is,
(Given the distance between the two slits S1 and S2 is 2λ)
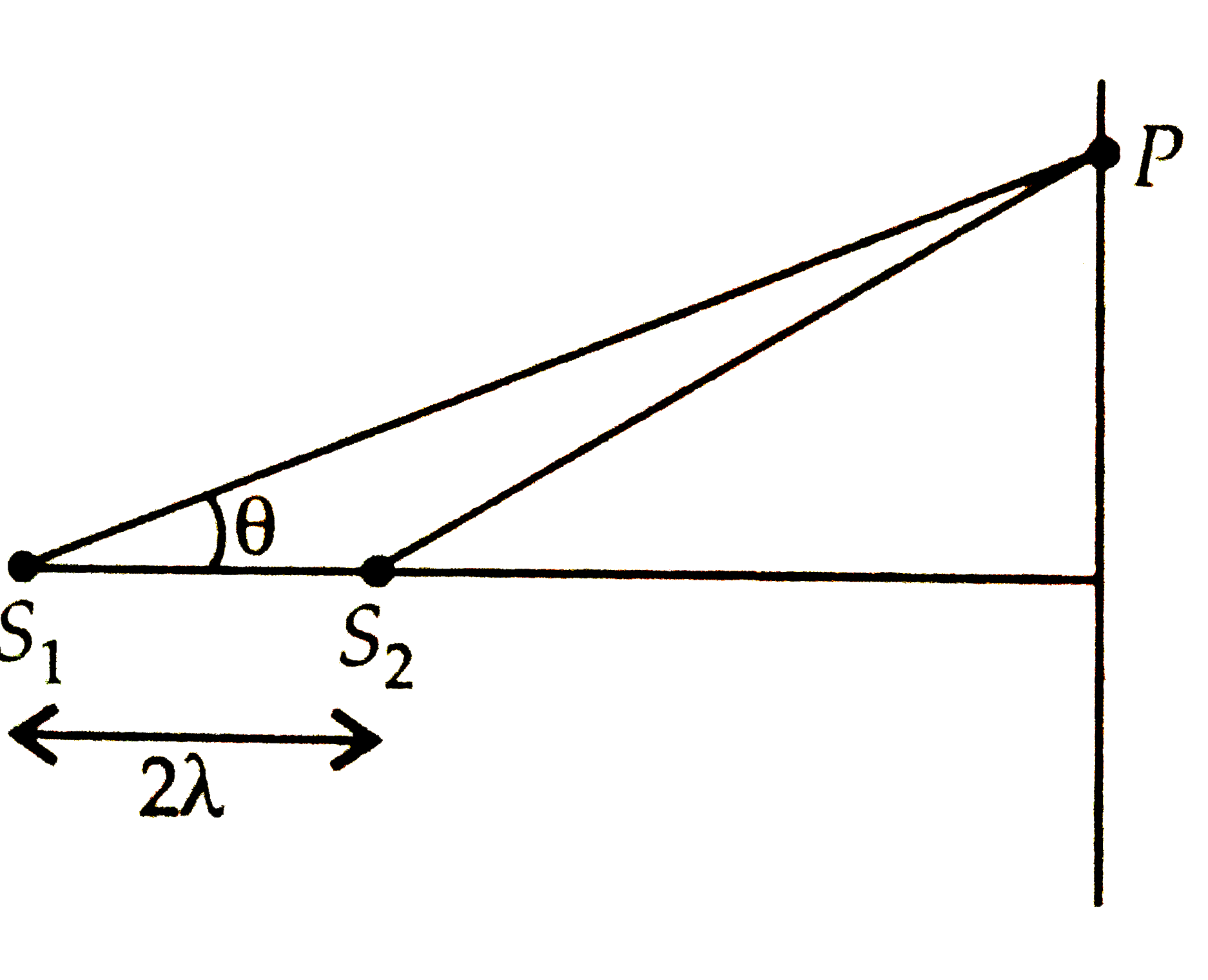 Acos−1(112)Bsin−1(112)Ctan−1(112)Dsin−1(35)
Acos−1(112)Bsin−1(112)Ctan−1(112)Dsin−1(35)
In a Young's double slit experiment, I0 is the intensity at the central maximum and β is the fringe width. The intensity at a point P distant x from the centre will be
View SolutionIn the standard Young's double slit experiment, the intensity on the screen at a point distant 1.25 fringe widths from the central maximum is (assuming slits to be identical)
View SolutionIn the Young's double slit experiment, the spacing between two slits is 0.1mm. If the screen is kept at a distance of 1.0m from the slits and the wavelength of ligth is 5000Å, then the fringe width is
View SolutionIn Young's double-slit experiment, the intensity at a point P on the screen is half the maximum intensity in the interference pattern. If the wavelength of light used is λ and d is the distance between the slits, the angular separation between point P and the center of the screen is
View SolutionIn a Young's double-slit expriment using identical slits, the intensity at a bright fringe is I_(0). If one of the slits is now covered, the intensity at any point on the screen will be
View SolutionThe intensity of each of the two slits in Young's double slit experiment is I0 Calculate the minimum separation between the two points on the screen where intensities are 2I0 and I0 Given the fringe width equal to α
View Solution