In an uniform electric field of strength E, a charge particle Q moves point A to point B in the direction of the field and back from B to A. Calculate the ratio of the work done by the electric field in taking the charge particle from A to B and from B to A.

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem of calculating the ratio of work done by the electric field when a charged particle moves from point A to point B and back from point B to point A, we can follow these steps:
1. Understanding the Electric Field:
- We have a uniform electric field $E$ directed from point A to point B.
- A charge $Q$ is moved from A to B in the direction of the electric field.
2. Work Done from A to B:
- When the charge $Q$ moves from A to B, the work done by the electric field $W_{1}$ can be calculated using the formula:
$W_{1} = F \cdot d \cdot cos (θ)$
- Here, $F$ is the force acting on the charge due to the electric field, $d$ is the distance between A and B, and $θ$ is the angle between the force and the displacement.
- Since the force $F = Q \cdot E$ acts in the same direction as the displacement, $θ = 0^{\circ}$ and $cos (0) = 1$ .
- Therefore, the work done from A to B is:
$W_{1} = Q \cdot E \cdot d \cdot 1 = Q \cdot E \cdot d$
3. Work Done from B to A:
- When the charge $Q$ moves back from B to A, the work done by the electric field $W_{2}$ is calculated similarly:
$W_{2} = F \cdot d \cdot cos (θ)$
- In this case, the force $F = Q \cdot E$ is still in the direction of the electric field, but the displacement is in the opposite direction. Thus, $θ = 180^{\circ}$ and $cos (180) = - 1$ .
- Therefore, the work done from B to A is:
$W_{2} = Q \cdot E \cdot d \cdot (- 1) = - Q \cdot E \cdot d$
4. Calculating the Ratio:
- We need to find the ratio of the work done from A to B and from B to A:
$\frac{W_{1}}{W_{2}} = \frac{Q \cdot E \cdot d}{- Q \cdot E \cdot d}$
- Simplifying this gives:
$\frac{W_{1}}{W_{2}} = - 1$
Final Result:
The ratio of the work done by the electric field in taking the charge particle from A to B and from B to A is:
$\frac{W_{1}}{W_{2}} = - 1$

Updated on:18/9/2024

If the test charge is moved back to R from P, then work done by electric field is
A3 J
Bzero
Ccannot be determined
DNone of the above
A charged particle moving in an electric field
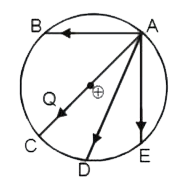
Amust undergo change in velocity
Bmust undergo change in speed
Cmay not undergo change in velocity
Dmay not undergo change in speed
In the electric field of a point chargde $q$ , a cetrain charge is carried from point $A$ to $B, C, D$ and $E$ . Then the ork done

Ais least along the path $A B$
Bis least along the path $A D$
Cis zero along all the paths $A B, A C, A D and A E$
Dis least along $A E$