In case of linearly polarised light, the magnitude of the electric field vector
is parallel to the direction of propagation
does not change with time
increases linearly with time
varies perodically with time
The correct Answer is:D
To solve the question regarding the magnitude of the electric field vector in the case of linearly polarized light, we can follow these steps:
1. Understanding Polarization:
- Polarization is a phenomenon that restricts the vibrations of the electric field vector of light waves to a particular direction. In the case of linearly polarized light, the electric field oscillates in a single plane.
Hint: Remember that polarization affects the direction of the electric field vector.
2. Electric Field Vector in Electromagnetic Waves:
- Light can be described as an electromagnetic wave, which consists of oscillating electric and magnetic fields. The electric field vector (E) varies with time and space.
Hint: Recall that electromagnetic waves consist of both electric and magnetic fields that oscillate perpendicular to each other.
3. Variation of the Electric Field Vector:
- For linearly polarized light, the electric field vector can be expressed mathematically as:
E(t)=E0sin(ωt+ϕ)
where E0 is the maximum amplitude, ω is the angular frequency, t is time, and ϕ is the phase constant. This equation shows that the electric field varies sinusoidally with time.
Hint: Consider how the sine function represents periodic motion.
4. Conclusion on the Magnitude of the Electric Field Vector:
- Since the electric field vector varies sinusoidally with time, we conclude that the magnitude of the electric field vector in linearly polarized light varies periodically.
Hint: Think about how periodic functions repeat their values at regular intervals.
5. Final Answer:
- The correct answer is that the magnitude of the electric field vector varies periodically with respect to time.
Summary:
The electric field vector of linearly polarized light oscillates in a single direction and varies periodically over time, reflecting the nature of electromagnetic waves.
- Polarization is a phenomenon that restricts the vibrations of the electric field vector of light waves to a particular direction. In the case of linearly polarized light, the electric field oscillates in a single plane.
- Light can be described as an electromagnetic wave, which consists of oscillating electric and magnetic fields. The electric field vector (E) varies with time and space.
- For linearly polarized light, the electric field vector can be expressed mathematically as:
E(t)=E0sin(ωt+ϕ)
where E0 is the maximum amplitude, ω is the angular frequency, t is time, and ϕ is the phase constant. This equation shows that the electric field varies sinusoidally with time.
- Since the electric field vector varies sinusoidally with time, we conclude that the magnitude of the electric field vector in linearly polarized light varies periodically.
- The correct answer is that the magnitude of the electric field vector varies periodically with respect to time.
The electric field vector of linearly polarized light oscillates in a single direction and varies periodically over time, reflecting the nature of electromagnetic waves.
Topper's Solved these Questions
- WAVE OPTICSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - HIGHER ORDER THINKING SKILLS
8 Videos
- WAVE OPTICSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - NCERT EXEMPLAR PROBLEMS
5 Videos
- SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS EXERCISE - Assertion And Reason
15 Videos
Similar Questions
A : In an EM wave the magnitude of the electric field vector is more than the magnitude of the magnetic field vector.
R : Energy of the EM wave is shared equally between the electric and magnetic fields.
View Solutiona proton placed in an electric field would experience an electrical force equal to its weight. the magnitude of electric field intensity E would be
View SolutionImagine a short diploe at the center of a spherical surface. If the magnitude of the electric field at a certain point on the surface of he sphere is 10NC_1 then which of the following cannot be the magnitude of the electric field anywhere on the surface of the sphere?
View SolutionThe maximum electric field at a point on the axis of a uniformly charged ring is E0. At how many points on the axis will the magnitude of the electric field be E0/2.
View SolutionAt which distance along the centre axis of a uniformaly charged plastic disc of radius R is the magnitude of the electric field equal to one-half the magnitude of the field at the centre of the surface of the disc ?
View SolutionAssertion: If we see along the axis of a chaged ring, the magnitudeof electric field is minimum at centre and magnitude of electridc potential is maximum.
Reason: Electric field is a vector quantity while electric potential is scalar.
View Solutiondefine plane polarised light in short ?
View SolutionA cylindrical region of radius R contains a uniform magnetic field parallel to axis with magnitude that is changing linearly with time. If r is the radial distance of a point from axis of cylinder in a plane perpendicular to axis then the magnitude of the induced electrical field outside the cylinder is directly proportional to
View SolutionConsider the following two statements regarding a linearly polarized, plane electromagnetic wave:
The electric field and the magnetic field have equal average values.
The electric energy and the magnetic energy have equal average values.
View SolutionIn fig, two particles, each of charge -q are arranged symmetrically about the y-axis, each producing an electric field at point P on the y-axis.
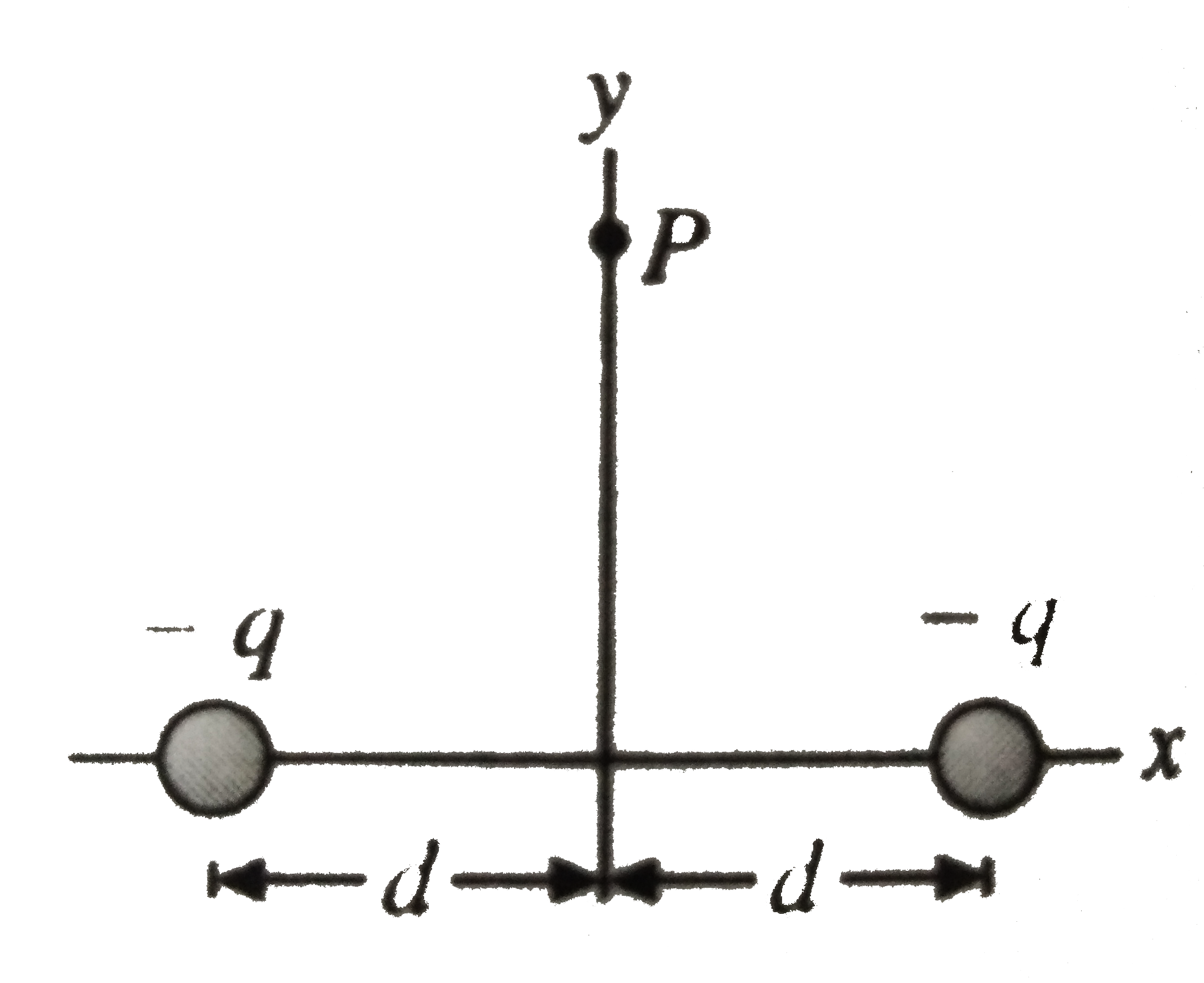 .
.
(a) Are the magnitudes of the fields at P equal?
(b) Is each electric field directed towards or away form the charge producing it ?
(c ) Is the magnitude of the net electric field at P equal to the sum of the magnitudes E of the two field vectors (is it equal to 2E)?
(d) Do the x-components of those two field vectors add or cancel?
(e ) Do their y-components add or cancel?
(f) Is the diretion of the net field at P that of the canceling components or the adding components?
(g) What is the direction of the net field?
View Solution
