In charging singe loop R - C circuit, after how many time constant, the potential energy in the capacitor will be 25% of its maximum value.
To solve the problem of determining how many time constants it takes for the potential energy in a capacitor to reach 25% of its maximum value in a charging single loop R-C circuit, we can follow these steps:
1. Understand the Formula for Potential Energy in a Capacitor:
The potential energy U stored in a capacitor at any time t is given by:
U=q22C
where q is the charge on the capacitor and C is the capacitance.
2. Identify the Maximum Potential Energy:
The maximum potential energy U0 when the capacitor is fully charged (with charge Q) is:
U0=Q22C
3. Set Up the Equation for 25% of Maximum Potential Energy:
We want to find when the potential energy U is 25% of the maximum potential energy:
U=0.25U0=14⋅Q22C=Q28C
4. Relate Charge q to Maximum Charge Q:
The charge q on the capacitor at time t is given by:
q(t)=Q(1−e−t/τ)
where τ is the time constant of the circuit.
5. Substitute q(t) into the Potential Energy Formula:
Substitute q(t) into the potential energy formula:
U=(Q(1−e−t/τ))22C
6. Set the Potential Energy Equal to 25% of Maximum Energy:
Equate the potential energy to Q28C:
(Q(1−e−t/τ))22C=Q28C
7. Simplify the Equation:
Cancel Q22C from both sides:
(1−e−t/τ)2=14
8. Take the Square Root:
Taking the square root of both sides gives:
1−e−t/τ=12
9. Solve for e−t/τ:
Rearranging gives:
e−t/τ=12
10. Take the Natural Logarithm:
Taking the natural logarithm of both sides:
−tτ=ln(12)
11. Solve for t:
Thus, we have:
t=−τln(12)=τln(2)
12. Calculate the Time in Terms of Time Constant:
Knowing that ln(2)≈0.693:
t≈0.693τ
Final Answer:
The time taken for the potential energy in the capacitor to reach 25% of its maximum value is approximately 0.693τ.
The potential energy U stored in a capacitor at any time t is given by:
U=q22C
where q is the charge on the capacitor and C is the capacitance.
The maximum potential energy U0 when the capacitor is fully charged (with charge Q) is:
U0=Q22C
We want to find when the potential energy U is 25% of the maximum potential energy:
U=0.25U0=14⋅Q22C=Q28C
The charge q on the capacitor at time t is given by:
q(t)=Q(1−e−t/τ)
where τ is the time constant of the circuit.
Substitute q(t) into the potential energy formula:
U=(Q(1−e−t/τ))22C
Equate the potential energy to Q28C:
(Q(1−e−t/τ))22C=Q28C
Cancel Q22C from both sides:
(1−e−t/τ)2=14
Taking the square root of both sides gives:
1−e−t/τ=12
Rearranging gives:
e−t/τ=12
Taking the natural logarithm of both sides:
−tτ=ln(12)
Thus, we have:
t=−τln(12)=τln(2)
Knowing that ln(2)≈0.693:
t≈0.693τ
The time taken for the potential energy in the capacitor to reach 25% of its maximum value is approximately 0.693τ.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Subjective29videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Single Correct72videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Exercise 5.128videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits15videos
ELECTRIC CURRENT & CIRCUITS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s38videos
ELECTRIC FLUX AND GAUSS LAW
Similar Questions
Find the time after which current in the circuit becomes 80% of its maximum value
View SolutionHow many time constants will elapse before the charge on a capacitor falls to 0.1%of its maximum value in a discharging RC circuit.
View SolutionIn C−R circuit, answer the following two questions
During charging of C−R circuit let t1 and i1 be the time constant and initial charging current when capacitor is assumed to be filled by a perfect insulator and t2 and i2 be the corresponding values when it is assumed imperfect. ThenView SolutionHow many time constant will elapse before the power delivered by the battery drops to half of its maximum value in RC circuit.
View Solutionhow many time constants will elapse before the power delovered by the battery drops to half of its maximum value in an RC circuit ?
View SolutionIn the circuit of figure, the battery emf is ε the resitance is R and the capacitance is C. The switch S is closed for a long time interval, and zero potential difference is measured across the capacitor

After the switch is opened. the potential difference across the capacitor reaches a maximum value of ΔV. What is the value of the inductance?View SolutionLet C be the capacitance of a capacitor discharging through a resistor R. Suppose t1 is the time taken for the energy stored in the capacitor to reduce to half its initial value and t2 is the time taken for the charge to reduce to one-fourth its initial value. Then the ratio t1/t2 will be
View SolutionFind the charge and energy stored on the capacitor C in the following circuit.
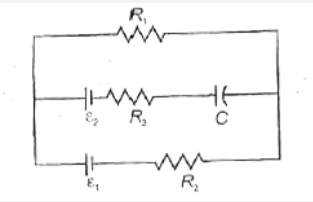 View Solution
View SolutionIn an oscillating L−C circuit in which C=4.00μF, the maximum potential difference capacitor during the oscillations is 1.50V and the maximum current through 50.0mA.
(a) What is the inductance L?
(b) What is the frequency of the oscillations?
(c) How much time does the charge on the capacitor take to rise from zero to its maximum value?View SolutionIn a decaying L−R circuit, the time after which energy stores in the inductor reduces to one fourth of its initial values is
View Solution

