Find the time after which current in the circuit becomes 80% of its maximum value
ln2100
ln3100
ln5100
ln6100
The correct Answer is:C
To find the time after which the current in an LR circuit becomes 80% of its maximum value, we can follow these steps:
1. Understand the LR Circuit:
In an LR circuit, the current I(t) at time t is given by the formula:
I(t)=Imax(1−e−RLt)
where Imax is the maximum current, R is the resistance, and L is the inductance.
2. Set Up the Equation for 80% of Maximum Current:
We want to find the time t when the current I(t) is 80% of its maximum value:
I(t)=0.8Imax
3. Substitute into the Current Equation:
Substitute 0.8Imax into the current equation:
0.8Imax=Imax(1−e−RLt)
4. Cancel Imax:
Since Imax is common on both sides, we can cancel it out:
0.8=1−e−RLt
5. Rearranging the Equation:
Rearranging gives:
e−RLt=1−0.8=0.2
6. Taking the Natural Logarithm:
Taking the natural logarithm on both sides:
−RLt=ln(0.2)
7. Solving for Time t:
Rearranging for t:
t=−LRln(0.2)
8. Substituting Values:
If we have R=1Ω and L=10mH=10×10−3H:
t=−10×10−31ln(0.2)
9. Calculating ln(0.2):
We know that ln(0.2)≈−1.6094:
t=−10×10−3×(−1.6094)=10×10−3×1.6094≈0.016094s
10. Final Answer:
Thus, the time after which the current becomes 80% of its maximum value is approximately:
t≈0.0161s
In an LR circuit, the current I(t) at time t is given by the formula:
I(t)=Imax(1−e−RLt)
where Imax is the maximum current, R is the resistance, and L is the inductance.
We want to find the time t when the current I(t) is 80% of its maximum value:
I(t)=0.8Imax
Substitute 0.8Imax into the current equation:
0.8Imax=Imax(1−e−RLt)
Since Imax is common on both sides, we can cancel it out:
0.8=1−e−RLt
Rearranging gives:
e−RLt=1−0.8=0.2
Taking the natural logarithm on both sides:
−RLt=ln(0.2)
Rearranging for t:
t=−LRln(0.2)
If we have R=1Ω and L=10mH=10×10−3H:
t=−10×10−31ln(0.2)
We know that ln(0.2)≈−1.6094:
t=−10×10−3×(−1.6094)=10×10−3×1.6094≈0.016094s
Thus, the time after which the current becomes 80% of its maximum value is approximately:
t≈0.0161s
Topper's Solved these Questions
Similar Questions
If maximum energy is stored in capacitor at t = 0 then find the time after which current in the circuit will be maximum.
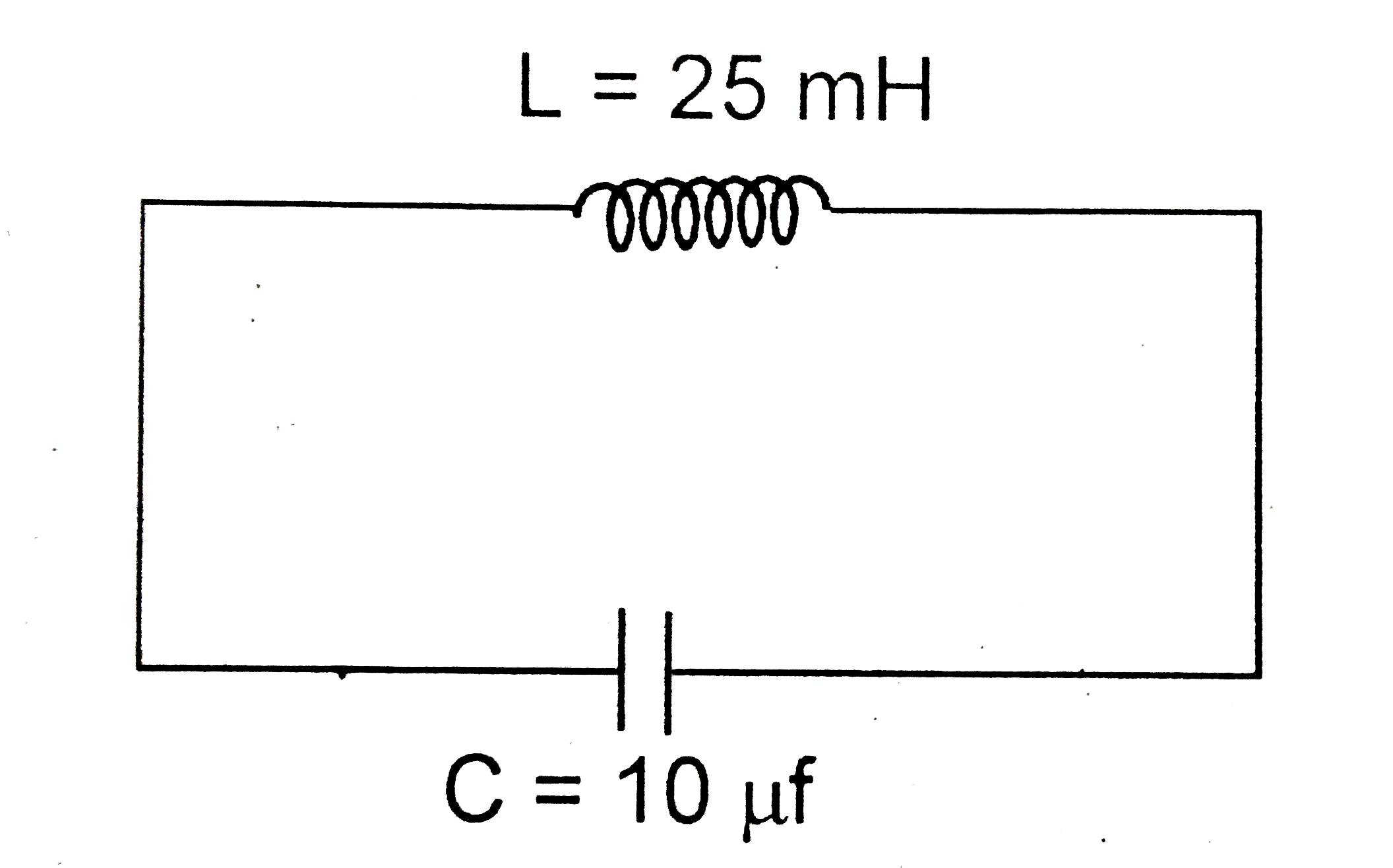
View SolutionA charged capacitro and an inductor are connected in series. At time t = 0 , the current is zero but the capacitor is charged, If T is the period of resulting oscillations, then the time after which current in the circuit becomes maximum , is
View SolutionA circuit consists of a coil, a switch and a battery, all in series. The internal resistance of the battery is negligible compared with that of the coil. The switch is originally open. It is thrown closed, after a time interval Δt. The current in the circuit reaches 80.0% of its final value. The switch then remains closed for a time interval much longer than Δt. The wires connected to the terminals of the battery are then short circuited with another wire and removed from the battery, so that the current is uninterrupted.
At an instant that is a time interval Δt. After the short circuit, the current is what percentage of its maximum value? a)20% b) 8% c) 4% d)10 %
View SolutionIf at t = 0 the switch Sw is closed , then the charge on capacitor (initially unchanged)in the given circuit when the current through battery becomes 50 % of its maximum value is (assume battery is ideal)

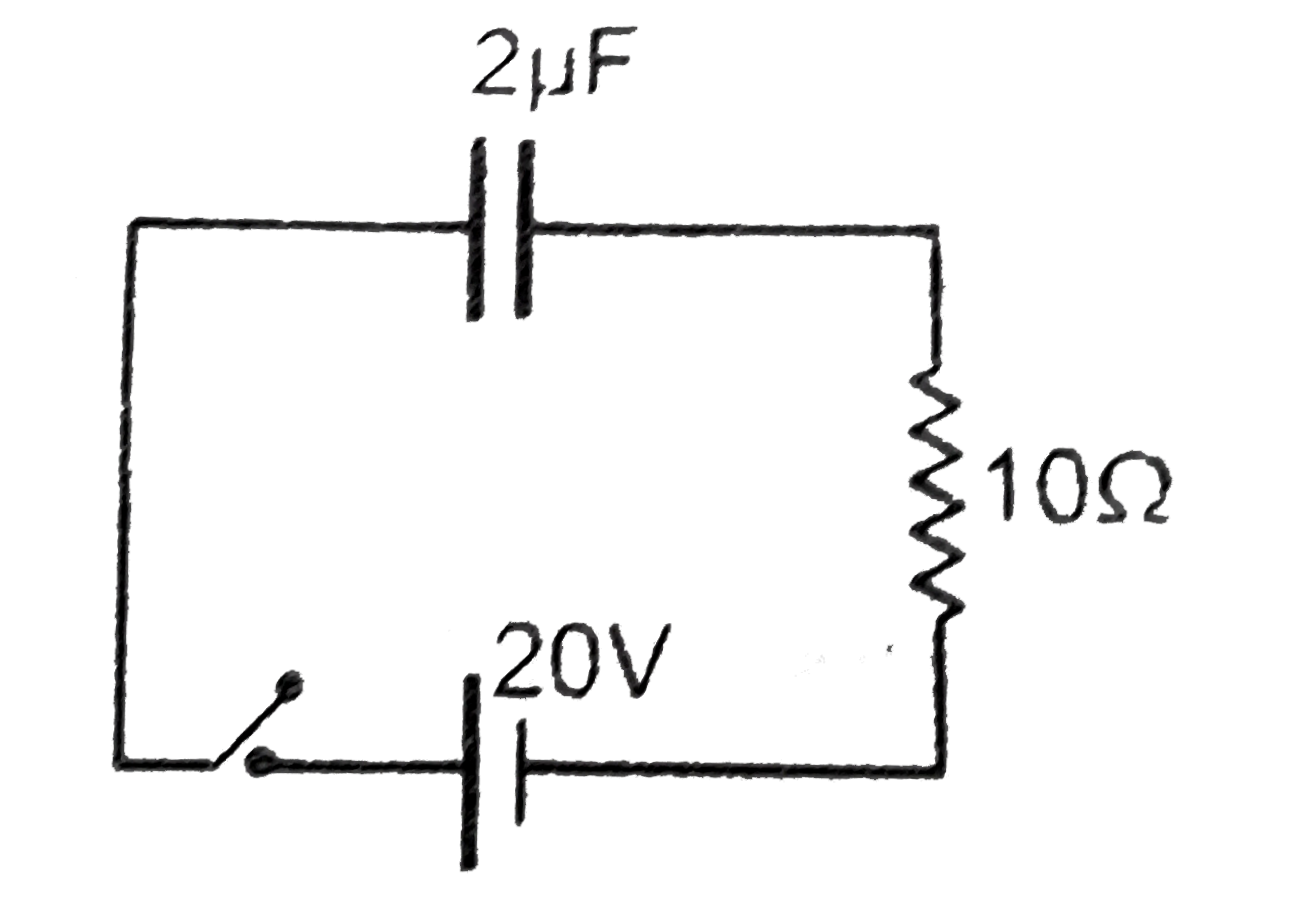
View SolutionInitially capacitor is uncharged at t=0 switch is closed. Charge on capacitor when current in the circuit is 10% of maximum current :
View SolutionThe magnetic field at a point inside a 2.0 mH inductor coil becomes 0.80 of its maximum value in 20μs when the inductor is joined to a battery. Find the resistance of the circuit.
View SolutionThe magnetic field at a point inside a 2.0 mH inductor coil becomes 0.80 of its maximum value in 20μs when the inductor is joined to a battery. Find the resistance of the circuit.
View SolutionA resistance of 20Ω is connected to a source of alternating current rated 110V,50Hz. Find (a) the rms current, (b) the maximum instantaneous current in the resistor and (c) the time taken by the current to change from its maximum value to the rms value.
View SolutionIn charging singe loop R - C circuit, after how many time constant, the potential energy in the capacitor will be 25% of its maximum value.
View SolutionIn a decaying L−R circuit, the time after which energy stores in the inductor reduces to one fourth of its initial values is
View Solution
