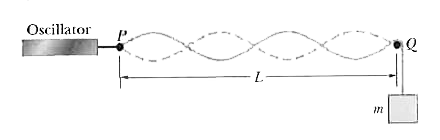
In Fig. 16-45, a string, tied to a sinusoidal oscillator at P and running over a support at Q, is stretched by a block of mass m. The separation L between P and Q is 1.20 m, and the frequency f of the oscillator is fixed at 120 Hz. The amplitude of the motion at P is small enough for that point to be considered a node. A node also exists at Q. A standing wave appears when the mass of the hanging block is 286.1 g or 4470g, but not for any intermediate mass. What is the linear density of the string?
The correct Answer is:0.845 g/m
Topper's Solved these Questions
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Single Correct Choice Type)
33 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (More than One Coorect Choice Type)
10 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Checkpoint
8 Videos
- WAVE - IIBOOK - RESNICK AND HALLIDAYCHAPTER - WAVE - IIEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)
5 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (Integer Type)
5 Videos
Similar Questions
In Fig 16-45, a string, tied to a sinusoidal oscillator at P and running over a support at Q, is strecthed by a block of mass m, Separation, L=1,20m,l linear density μ=1.20g/m, and the oscilator frequency f=120Hz. The amplitude of the motion at P is small enough for that point to be considered a node. A node also exists at Q. (a) What mass m allows the osciallator to set up the fourth harmonic on the string? (b) What standing wave mode, if any can be set up if m=1.00kg?
View SolutionFind the frequency of small oscillations of thin uniform vertical rod of mass m and length l hinged at the point O.

View Solution
Knowledge Check
The mass M shown in the figure oscillates in simple harmnonic motion and amplitude A. The amplitude of the point P is
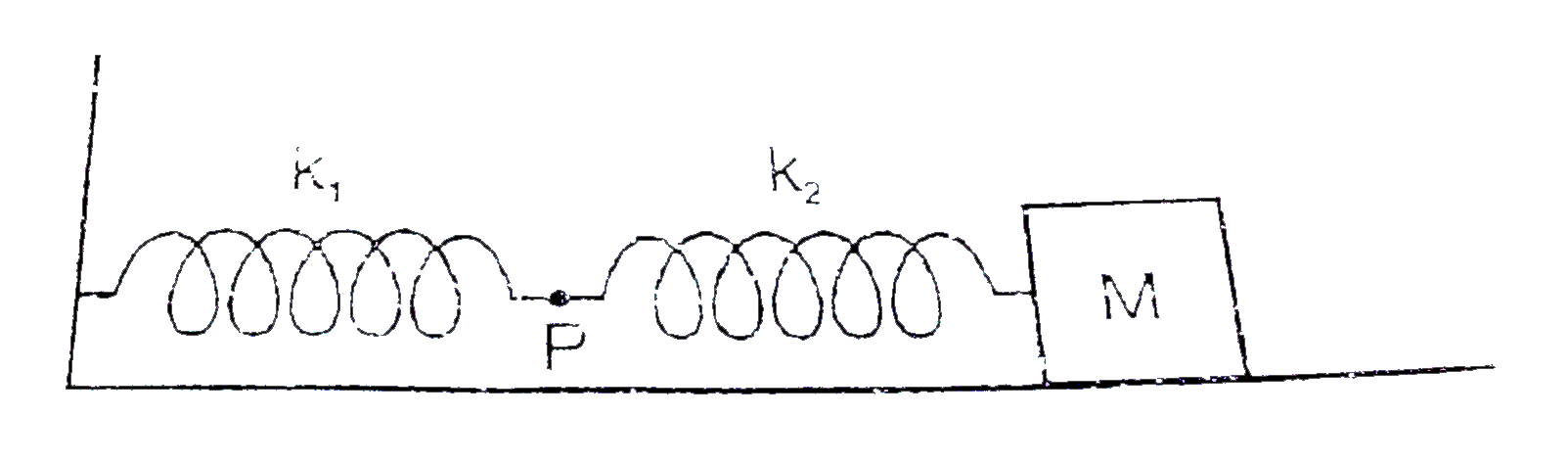 Ak1Ak2Bk2Ak1Ck1Ak1+k2Dk2Ak1+k2
Ak1Ak2Bk2Ak1Ck1Ak1+k2Dk2Ak1+k2A block of mass ‘m’ rests on a piston executing S.H.M. of period 1sec. The amplitude of oscillations so that the mass is separated from the piston is
A0.25 mB0.5 mC1mDzeroA simple harmonic oscillator has a frequency of 2.5 Hz and an amplitude of 0.05m. What is the period of the oscillations?
A0.4sB0.2sC8sD20s
A string, fixed at both ends, vibrates in a resonant mode with a separation of 2.0 cm between the consecutive nodes. For the next higher resonant frequency, this separation is reduced to 1.6 cm. Find the length of the string.
View SolutionA string, fixed at both ends, vibrates in a resonant mode with a separation of 2.0 cm between the consecutive nodes. For the next higher resonant frequency, this separation is reduced to 1.6 cm. Find the length of the string.
View SolutionThe resultant R of vector P andQ is perpendicular to P and R=P both , then angle betwwen |P|and|Q|is
View SolutionA uniform string fixed at both ends vibrates in a resonant mode with a separation of 2.0 cm between the consecutive nodes. For next higher resonant frequency, this separation is reduced to 1.6 cm. The length of the string is
View SolutionStanding waves are established on a string of length L such that A is a node and B is an immediate anti node. Oscillation amplitude of point B is a0. Let a' be the oscillation amplitude for point C. Pick the suitable option (s) for correct value of a' and the possible equation (s) for standing waves on the string.

View Solution
