In measuring time period of a pendulum, it is advised to measure the time between consecutive passage through the mean position in the same direction. This is said to result in better accuracy than measuring time between consecutive passage through an extreme position. Explain.
To explain why measuring the time period of a pendulum by observing its passage through the mean position in the same direction results in better accuracy than measuring the time between consecutive passages through an extreme position, we can break down the reasoning into several steps:
1. Understanding the Pendulum Motion:
- A simple pendulum swings back and forth in a periodic motion. The points where the pendulum changes direction are called extreme positions, and the point where it passes through the center is called the mean position.
2. Velocity at Different Positions:
- At the mean position, the pendulum has its maximum velocity. This is because all the potential energy has been converted into kinetic energy at this point.
- At the extreme positions, the pendulum momentarily comes to rest, meaning its velocity is nearly zero.
3. Measurement Accuracy:
- When measuring the time period by observing the pendulum at the mean position, the high speed of the pendulum allows for a clear and distinct observation of when the pendulum crosses this point.
- Conversely, at the extreme positions, the pendulum moves very slowly. This slow movement can lead to difficulty in accurately determining the exact moment when the pendulum reaches the extreme position, as the change in position is minimal.
4. Error in Timing:
- The slow speed at the extreme positions can introduce significant timing errors. For instance, if the observer is not precise in noting the exact moment the pendulum reaches the extreme position, the time measured could be longer or shorter than the actual time period.
- In contrast, the quick passage through the mean position reduces the chance of human error in timing, as the crossing is more pronounced and easier to observe.
5. Conclusion:
- Therefore, measuring the time between consecutive passages through the mean position in the same direction minimizes the potential for error and leads to a more accurate determination of the pendulum's time period compared to measuring at the extreme positions.
- A simple pendulum swings back and forth in a periodic motion. The points where the pendulum changes direction are called extreme positions, and the point where it passes through the center is called the mean position.
- At the mean position, the pendulum has its maximum velocity. This is because all the potential energy has been converted into kinetic energy at this point.
- At the extreme positions, the pendulum momentarily comes to rest, meaning its velocity is nearly zero.
- When measuring the time period by observing the pendulum at the mean position, the high speed of the pendulum allows for a clear and distinct observation of when the pendulum crosses this point.
- Conversely, at the extreme positions, the pendulum moves very slowly. This slow movement can lead to difficulty in accurately determining the exact moment when the pendulum reaches the extreme position, as the change in position is minimal.
- The slow speed at the extreme positions can introduce significant timing errors. For instance, if the observer is not precise in noting the exact moment the pendulum reaches the extreme position, the time measured could be longer or shorter than the actual time period.
- In contrast, the quick passage through the mean position reduces the chance of human error in timing, as the crossing is more pronounced and easier to observe.
- Therefore, measuring the time between consecutive passages through the mean position in the same direction minimizes the potential for error and leads to a more accurate determination of the pendulum's time period compared to measuring at the extreme positions.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises58videos
SIMPLE HARMONIC MOTION
- BOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer21videos
ROTATIONAL MECHANICS
- BOOK - HC VERMA ENGLISHCHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective-27videos
SOME MECHANICAL PROPERTIES OF MATTER
Similar Questions
Two simple pendulums have time period 4s and 5s respectively. If they started simultaneously from the mean position in the same direction, then the phase difference between them by the time the larger one completes one oscillation is
View SolutionA man measures time period of a pendulum (T) in stationary lift. If the lift moves upward with acceleration g4, then new time period will be
View Solution
Knowledge Check
- Question 1 - Select One
Figure shows the position-time (x-t) graph of one dimensional motion of a mass 500g. What is the time interval between two consecutive impulses received by the body?
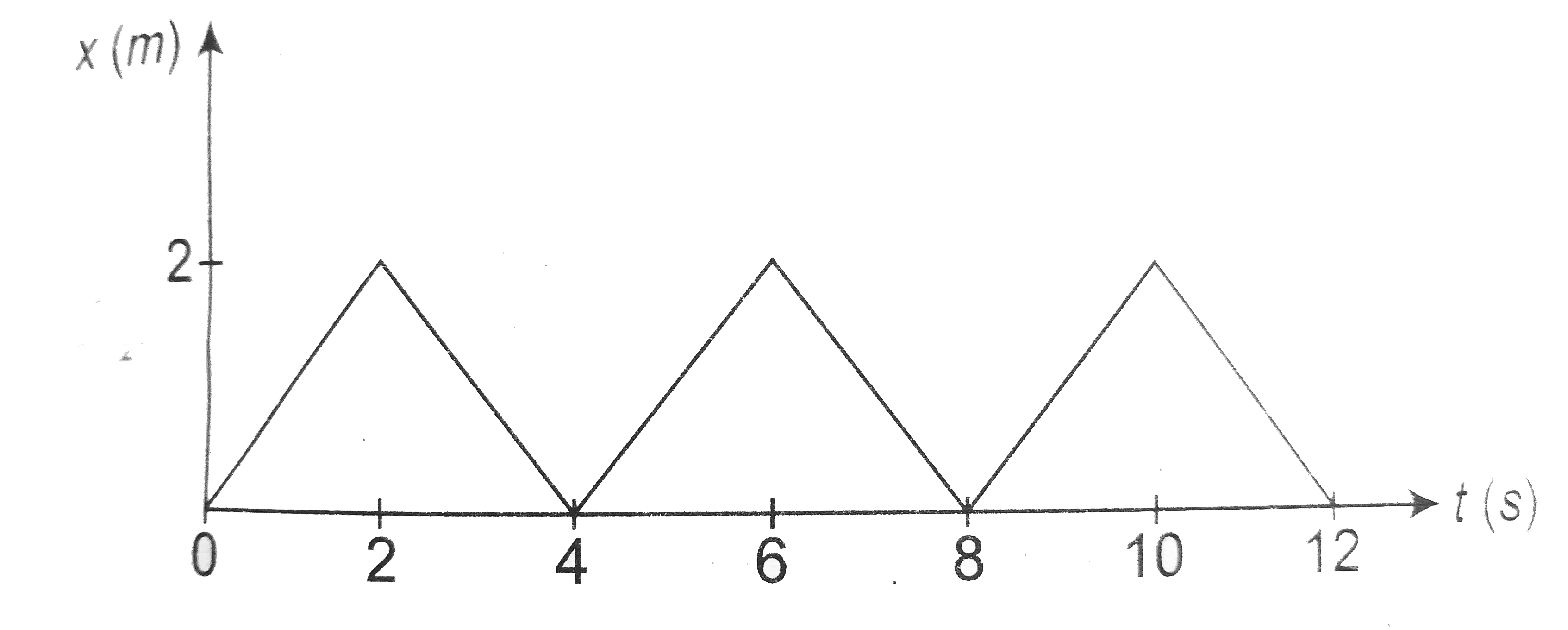 A2sB4sC6sD8s
A2sB4sC6sD8s
Two periodic waves of intensities I1 and I2 pass through a region at the same time in the same direction. The sum of the maximum and minimum intensities is:
View SolutionTwo periodic waves of intensities I1 and I2 pass through a region at the same time in the same direction. The sum of the maximum and minimum intensities is:
View SolutionThe time period of a simple pendulum of length L as measured in an elevator descending with acceleration g / 3 is
View SolutionThe kinetic energy of a particle executing shm is 32 J when it passes through the mean position. If the mass of the particle is.4 kg and the amplitude is one metre, find its time period.
View SolutionA particle executes shm of period.8 s. After what time of its passing through the mean position the energy will be half kinetic and half potential.
View SolutionA scientist measures the time period of a simple pendulum as T in a lift at rest. If the lift moves up with accelerationi as one fourth of the acceleratioin of gravity, the new time period is
 View Solution
View SolutionA simple pendulum suspended from the roof off a lift oscillates with frequency υ when the lift is at rest. If the lift falls freely under gravity, its frequency of oscillation becomes
View Solution

