In Melde's experiment a loaded string of lenyek Im weighing 0.5 gm khanging from a coming fork of thegoency 200 and is vibrating in four loops. Calculate the tension in string?
To calculate the tension in the string during Melde's experiment, we can use the formula for the frequency of a vibrating string. Here’s the step-by-step solution:
Step 1: Understand the Given Values
- Length of the string (L) = 1 meter
- Mass per unit length (μ) = 0.5 g/m = 0.5 × 10^(-3) kg/m
- Frequency of the fork (f) = 200 Hz
- Number of loops (N) = 4
Step 2: Write the Formula for Frequency
The frequency of a vibrating string can be given by the formula:
f=N2L√Tμ
Where:
- f = frequency
- N = number of loops (or harmonics)
- L = length of the string
- T = tension in the string
- μ = mass per unit length
Step 3: Rearrange the Formula to Solve for Tension (T)
We need to isolate T in the formula. Squaring both sides gives:
f2=(N2L)2Tμ
Rearranging gives:
T=f2⋅4L2⋅μN2
Step 4: Substitute the Known Values into the Formula
Now, substitute the known values into the equation:
- f=200 Hz
- L=1 m
- μ=0.5×10−3 kg/m
- N=4
So, we have:
T=(200)2⋅4⋅(1)2⋅(0.5×10−3)(4)2
Step 5: Simplify the Equation
Calculating the components:
- (200)2=40000
- 4⋅(1)2=4
- (4)2=16
Now substituting these values:
T=40000⋅4⋅0.5×10−316
Step 6: Calculate the Tension
Now, calculate:
T=40000⋅4⋅0.5×10−316=80000×10−316=8016=5 N
Final Answer
The tension in the string is 5 Newtons.
---
- Length of the string (L) = 1 meter
- Mass per unit length (μ) = 0.5 g/m = 0.5 × 10^(-3) kg/m
- Frequency of the fork (f) = 200 Hz
- Number of loops (N) = 4
The frequency of a vibrating string can be given by the formula:
f=N2L√Tμ
Where:
- f = frequency
- N = number of loops (or harmonics)
- L = length of the string
- T = tension in the string
- μ = mass per unit length
We need to isolate T in the formula. Squaring both sides gives:
f2=(N2L)2Tμ
Rearranging gives:
T=f2⋅4L2⋅μN2
Now, substitute the known values into the equation:
- f=200 Hz
- L=1 m
- μ=0.5×10−3 kg/m
- N=4
T=(200)2⋅4⋅(1)2⋅(0.5×10−3)(4)2
Calculating the components:
- (200)2=40000
- 4⋅(1)2=4
- (4)2=16
T=40000⋅4⋅0.5×10−316
Now, calculate:
T=40000⋅4⋅0.5×10−316=80000×10−316=8016=5 N
The tension in the string is 5 Newtons.
Topper's Solved these Questions
- WAVESBOOK - ICSECHAPTER - WAVESEXERCISE - Musical Sound
2 Videos
- WAVESBOOK - ICSECHAPTER - WAVESEXERCISE - Conceptual Short Answer Questions With Answers
25 Videos
- WAVESBOOK - ICSECHAPTER - WAVESEXERCISE - Additional Solved Problems
13 Videos
- VECTORS SCALARS ELEMENTARY CALCULUS BOOK - ICSECHAPTER - VECTORS SCALARS ELEMENTARY CALCULUS EXERCISE - UNSOLVED PROBLEMS
79 Videos
Similar Questions
Find the tension needed to produce stationary waves with 4 loops in a string 1m long and 0.5 gram in weight, fixed to a tuning fork of frequency 200Hz, when the prongs of the fork are vibrating perpendicular to the string.
View SolutionIn Melde's experiment when the tension is 100 gm and the fork vibrates at right angles to the direction of the string, the latter is thrown in four segments. If now the fork is set to vibrate along the string, find what additional load will make the string vibrate in one segment ?
View SolutionIn an experiment of standing waves, a string 90cm long is attached to the prong of an electrically driven tuning fork that scillates perpendicular to the length of the string at a frequency of 60Hz. The mass of the string is 0.044kg. What tension (in newton) must the string be under (weights are attached to the other end) if it is to oscillate in four loops?
View SolutionA lift starts from rest with a constant upward acceleration It moves 1.5 m in the first 0.4 A person standing in the lift holds a packet of 2 kg by a string Calculate the tension in the string during the motion .
View SolutionIn Melde's experiment it was found that the string vibrated in three loops wien 8 gm were placed on the scale pan. What mass must be placed on the pan to make the string vibrate in six loops? (Neglect the mass of the string and the scale pan]
View SolutionA string breaks under a load of 4.8kg A mass of 0.5 kg is attached to one end of a string 2 m long and is rotated in a horizontal circle . Calculate the greatest number of revolutions that the mass can make without breaking the string .
View SolutionIn Melde's experiment it was found that the string vibrated in 3 loops when 8gm were placed in a pan. What mass must be placed in the pan to make the string vibrate in 5 loops? (Neglect the mass of the string an the pan).
View SolutionIn Melde's experiment if there are two loops for one meter length in the longitudinal position, calculate the tension in the string. [Frequency of the fork is 128Hz and mass per unit length of the string is 5×10−6kg]. What will happen if the fork's is rotated through 90∘].
View SolutionA disc shaped pulley of mass 'm'=4kg and radius R=0.5m can rotate freely about its center. A block of mass M=2kg hangs from the pulley through is massless string that is tightly wrapped around the pulley. When the system is released, there is no slipping between pulley and string.
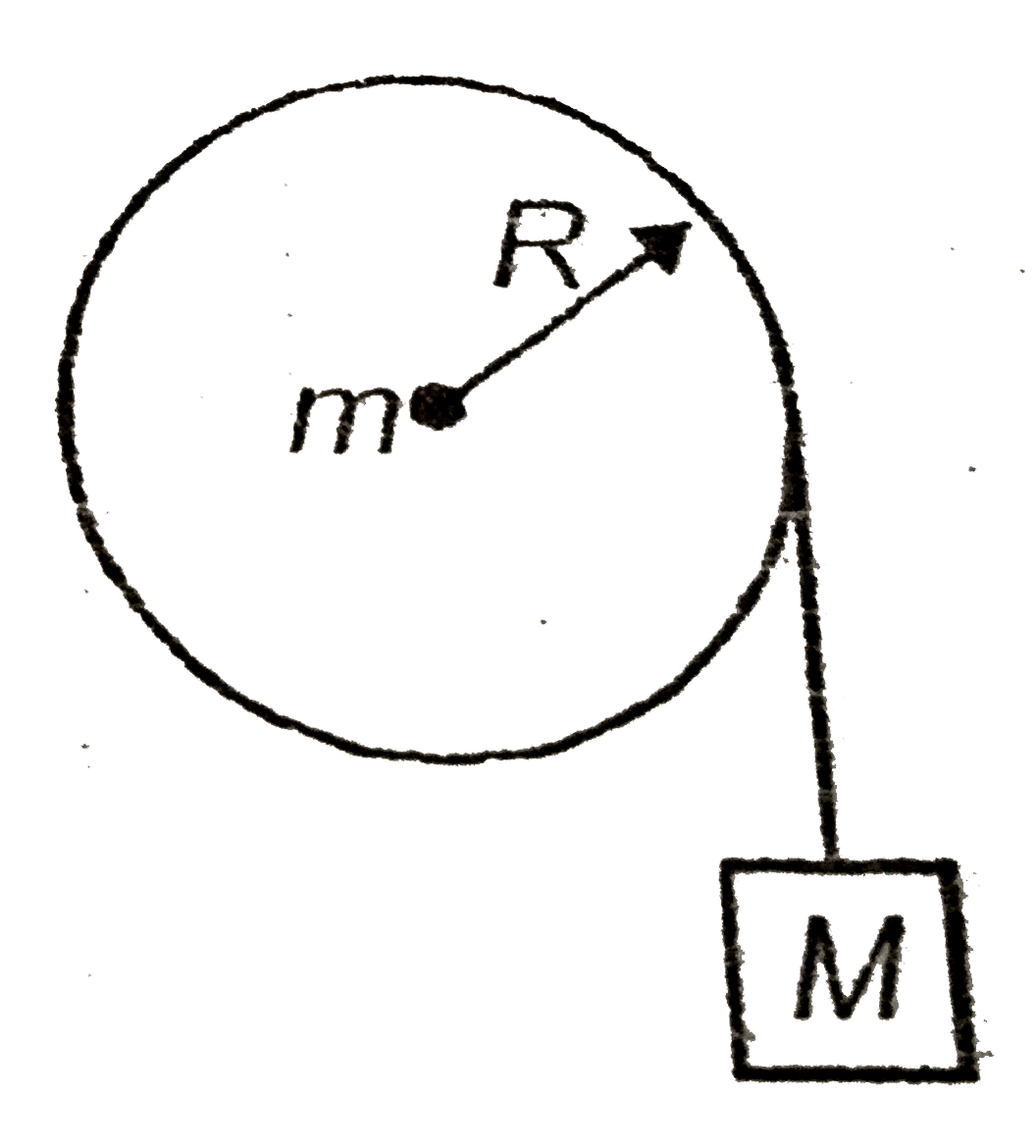
(a) Calculate the angular accelerating of the pulley
(b) Calculate the tension in the string
View SolutionA metal bob of mass 0.6 kg is attached to the end of a string of length 1 m and the bob is whirled in a horizontal circle with a uniform speed of 12 m/s. What is the centripetal force acting on the bob ? If the speed of the bob is 5 m/s calculate the tension in the string.
View Solution
