In SHM , the acceleration is ahead of velocity by a phase angle
0∘
π2
π
2π
The correct Answer is:B
As x=Asinωt
Velocity , v=Aωsin(ωt+π2) and the acceleration ,
a=Aω2sin(ωt+π)
Here, A=amplitude

∴ In SHM, the acceleration is ahead of velocity by a phase angle π2.
Similar Questions
Statement-1 : Frequency of kinetic energy of SHM is double that of frequency of SHM.
Statement-2. In SHM the velocity is ahead of displacement by a phase angle of π2.
View SolutionFor a particle in S.H.M. if the maximum acceleration is a and maximum velocity is v then amplitude is
View SolutionA wire is sliding as shown in Figure. The angle between the acceleration and the velocity of the wire is
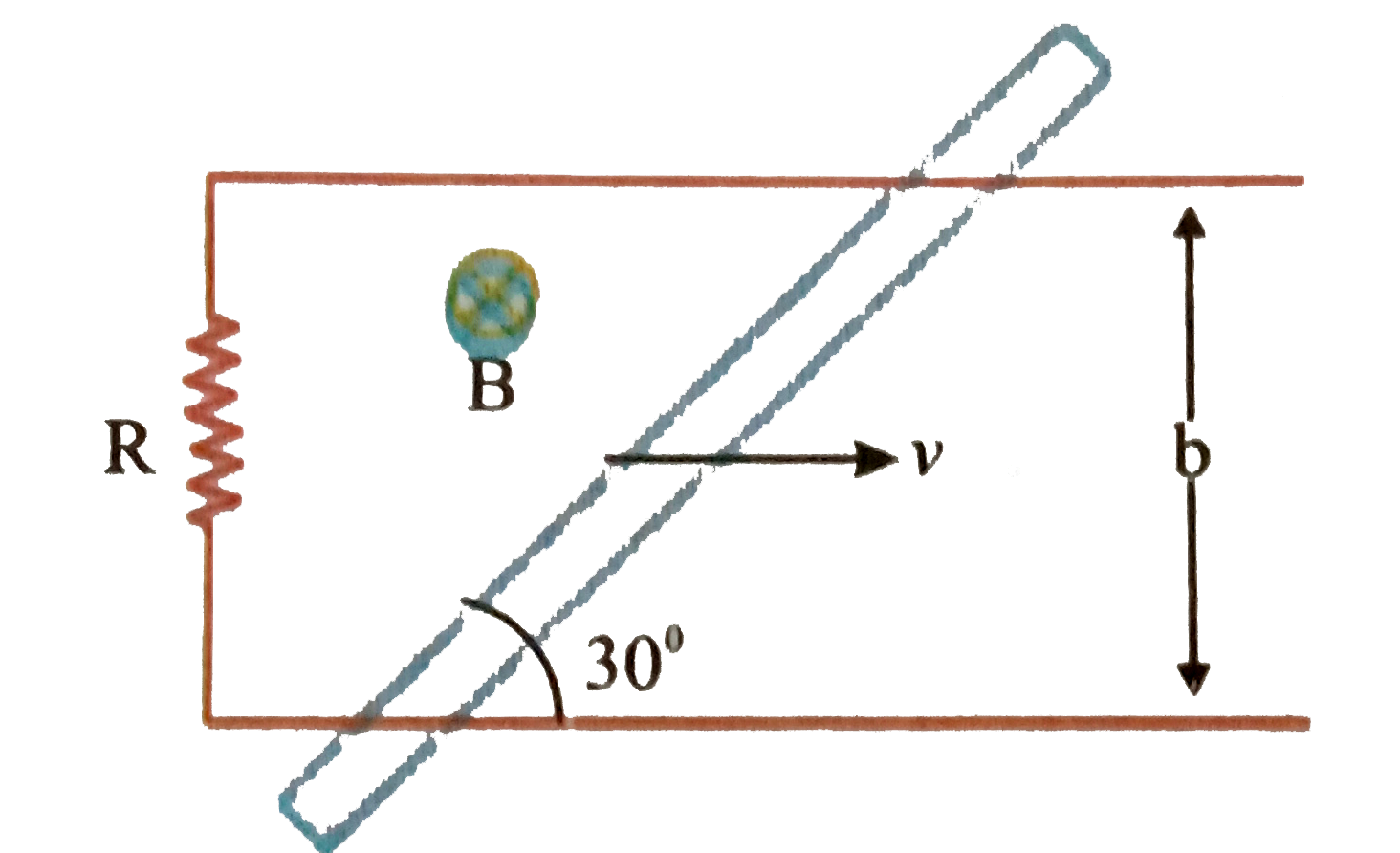
View SolutionGive examples where a. the velocity of a particle is zero but its acceleration is not zero. b.the velocity is opposite in direction to the acceleration, c. the velocity is perpendicular to the acceleration.
View SolutionA particle executes SHM on a straight line path. The amplitude of oscialltion is 3 cm. Magnitude of its acceleration is eqal to that of its velocity when its displacement from the mean position is 1 cm. Find the time period of S.H.M.
Hint :A=3cm
Whenx=1cm , magnitude of velocity =magnitude of acceleration
i.e., ω(A2−x2)(12)=ω2x
Find ω
T=(2π)(ω)
View SolutionGive examples for the particle where (a) the velocity is in opposite direction to the acceleration (b)the velocity of the particle is zero but is acceleration is not zero.
View SolutionFor any particle moving with some velocity (→v) & acceleration (→a), tangential acceleration & normal acceleration are defined as follows.
Tangential acceleration - The component of acceleration in the direction of velocity.
Normal acceleration - The component of acceleration in the direction perpendicular to velocity.
If at a given instant, velocity & acceleration of a particle are given by .
→c=4ˆi+3ˆj
→a=10ˆi+15ˆj+20ˆk
Find the tangential acceleration of the particle at the given instant :-
View SolutionThe acceleration of a body in SHM is
View SolutionIf a particle is executing S.H.M. then the graph between its acceleration and velocity is , in general
View SolutionFor Question , find maximum velocity and maximum acceleration
Hint : Maximum velocity =Aω
Maximum acceleration=Aω2
A particle executes SHM on a straight line path. The amplitude of oscillation is 3cm . magnitude of its acceleration is equal to that of its velocity when its displacement from the mean position is 1cm.
View Solution
