In the above problem, if the rod is released from horizontal position, the angular velocity of the rod as it passes the vertical position is (l=length fo rod)
√12g5l
√2g3l
√3gl
√3g7l
The correct Answer is:C
To solve the problem of finding the angular velocity of a rod as it passes the vertical position after being released from a horizontal position, we can follow these steps:
1. Identify the System:
- We have a uniform rod of length l that is hinged at one end and initially held in a horizontal position.
2. Determine the Initial and Final Positions:
- The initial position of the rod is horizontal, and the final position we are interested in is vertical.
3. Calculate the Change in Potential Energy:
- The center of mass of the rod is located at a distance of l2 from the hinge.
- When the rod is horizontal, its height relative to the lowest point (vertical position) is l2.
- The loss in gravitational potential energy (PE) as the rod moves from horizontal to vertical is given by:
ΔPE=mgh=mg⋅l2
4. Relate Potential Energy to Kinetic Energy:
- As the rod falls, the loss in potential energy is converted into kinetic energy (KE).
- The kinetic energy of a rotating body is given by:
KE=12Iω2
- For a rod rotating about one end, the moment of inertia I is:
I=13ml2
5. Set Up the Energy Conservation Equation:
- Equating the loss in potential energy to the gain in kinetic energy:
mg⋅l2=12(13ml2)ω2
6. Simplify the Equation:
- Cancel m from both sides (assuming m≠0):
g⋅l2=16l2ω2
- Multiply both sides by 6:
3gl=l2ω2
7. Solve for Angular Velocity ω:
- Rearranging gives:
ω2=3gl
- Taking the square root:
ω=√3gl
8. Final Result:
- The angular velocity of the rod as it passes the vertical position is:
ω=√3gl
Conclusion:
The correct answer is option C: √3gl.
- We have a uniform rod of length l that is hinged at one end and initially held in a horizontal position.
- The initial position of the rod is horizontal, and the final position we are interested in is vertical.
- The center of mass of the rod is located at a distance of l2 from the hinge.
- When the rod is horizontal, its height relative to the lowest point (vertical position) is l2.
- The loss in gravitational potential energy (PE) as the rod moves from horizontal to vertical is given by:
ΔPE=mgh=mg⋅l2
- As the rod falls, the loss in potential energy is converted into kinetic energy (KE).
- The kinetic energy of a rotating body is given by:
KE=12Iω2
- For a rod rotating about one end, the moment of inertia I is:
I=13ml2
- Equating the loss in potential energy to the gain in kinetic energy:
mg⋅l2=12(13ml2)ω2
- Cancel m from both sides (assuming m≠0):
g⋅l2=16l2ω2
- Multiply both sides by 6:
3gl=l2ω2
- Rearranging gives:
ω2=3gl
- Taking the square root:
ω=√3gl
- The angular velocity of the rod as it passes the vertical position is:
ω=√3gl
The correct answer is option C: √3gl.
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - A Only One Option is Correct
86 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
A uniform thin rod of length l and mass m is hinged at a distance l/4 from one of the end and released from horizontal position as shown in Fig. The angular velocity of the rod as it passes the vertical position is

View SolutionA rod of length L is hinged from one end. It is brought to the horizontal position and released. The angular velocity of the rod when it is in the vertical position is √Kg/L. Then find the value of K.
View SolutionA rod of length L is hinged from one end. It is brought to a horizontal position and released. The angular velocity of the rod, when it is in vertical position, is
View SolutionTwo particles each of mass m are attached at end points of a massless rod AB of length l. Rod is hinged at point C as shown. Rod is released from rest from horizontal position. At the instant when rod reaches its vertical position as shown, which of the following is / are correct:

View SolutionA uniform rod of maass m and length L is placed on the fixed cylindrical surface of radius R at an small angular position θ from the vertical (vertical means line joining centre and vertex of the cylindrical path) as shown in the figure and released from rest. Find the angular velocity ω of the rod at the instant when it crosses the horizontal position (Assume that when rod comes at horizontal position its mid point and vertex of the circular surface coincide). Friction is sufficient to prevent any slipping.

View SolutionA rod of length l is pivoted about a horizontal , frictionless pin through one end. The rod is released from ret in a vertical position. Find the velocity of the CM of the rod when the rod is inclined at an angle θ from the vertical.

View SolutionA uniform rod of length l is slightly disturbed from its vertical position. Find the angular velocity of the rod just after if hits the step. (Friction is sufficient everywhere to prevent slipping)

View SolutionIn space of horizontal EF(E=(mg)/q) exist as shown in figure and a mass m is released at the end of a light rod. If mass m is releases from the position shown in figure find the angular velocity of the rod when it passes through the bottom most position
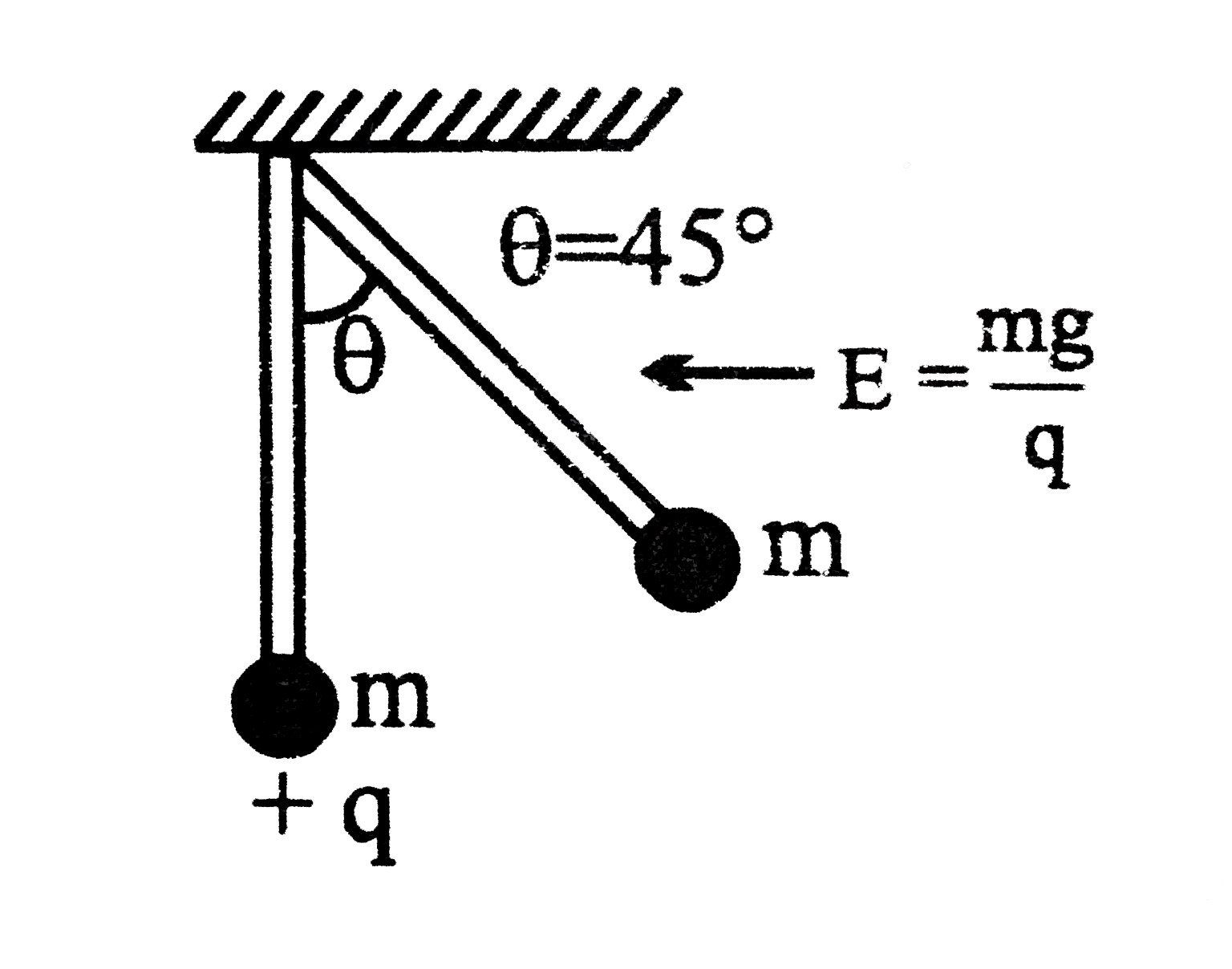 .
.
View SolutionIn the figure shown, the cart of mass 6m is initially at rest. A particle of mass in is attached to the end of the light rod which can rotate freely about A. If the rod is released from rest in a horizontal position shown, determine the velocity vrel of the particle with respect to the cart when the rod is vertical.

View SolutionA uniform rod of mass m, hinged at its upper end, is released from rest from a horizontal position. When it passes through the vertical position, the force on the hinge is
View Solution
