In the above question, if the velocity of the object on reaching the bottom is υ for the smooth plane andυn for the rough plane, then the coefficient of friction is given by :
μ=tanθ[1−1n2]
μ=cosθ[1−1n2]
μ=tanθ[1−1n2]12
μ=cosθ[1−1n2]12
The correct Answer is:a
Applying υ2−u2=2as we have υ2=2gsinθ×lor υ2=2gsinθ×l andυ2n2=2g(sinθ−μcosθ)l on
solving we get the same value of .u. as in the above question (a) is the choice
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - MODERN PUBLICATIONCHAPTER - LAWS OF MOTIONEXERCISE - MULTIPLE CHOICE QUESTION (LEVEL-II)
64 Videos
- LAWS OF MOTIONBOOK - MODERN PUBLICATIONCHAPTER - LAWS OF MOTIONEXERCISE - MULTIPLE CHOICE QUESTION (LEVEL-III)
2 Videos
- HEAT AND THERMODYNAMICSBOOK - MODERN PUBLICATIONCHAPTER - HEAT AND THERMODYNAMICSEXERCISE - Recent Competitve Questions
17 Videos
- MAGNETOSTATICSBOOK - MODERN PUBLICATIONCHAPTER - MAGNETOSTATICSEXERCISE - RECENT COMPETITIVE QUESTION
5 Videos
Similar Questions
A block moves down a smooth inclined plane of inclination θ. Its velocity on reaching the bottom is v. If it slides down a rough inclined plane of some inclination, its velocity on reaching the bottom is v/n, where n is a number greater than 0. The coefficient of friction is given by -
View SolutionA block is placed on the top of a plane inclined at 37∘ with horizontal. The length of the plane is 5m. The block slides down the plane and reaches the bottom.
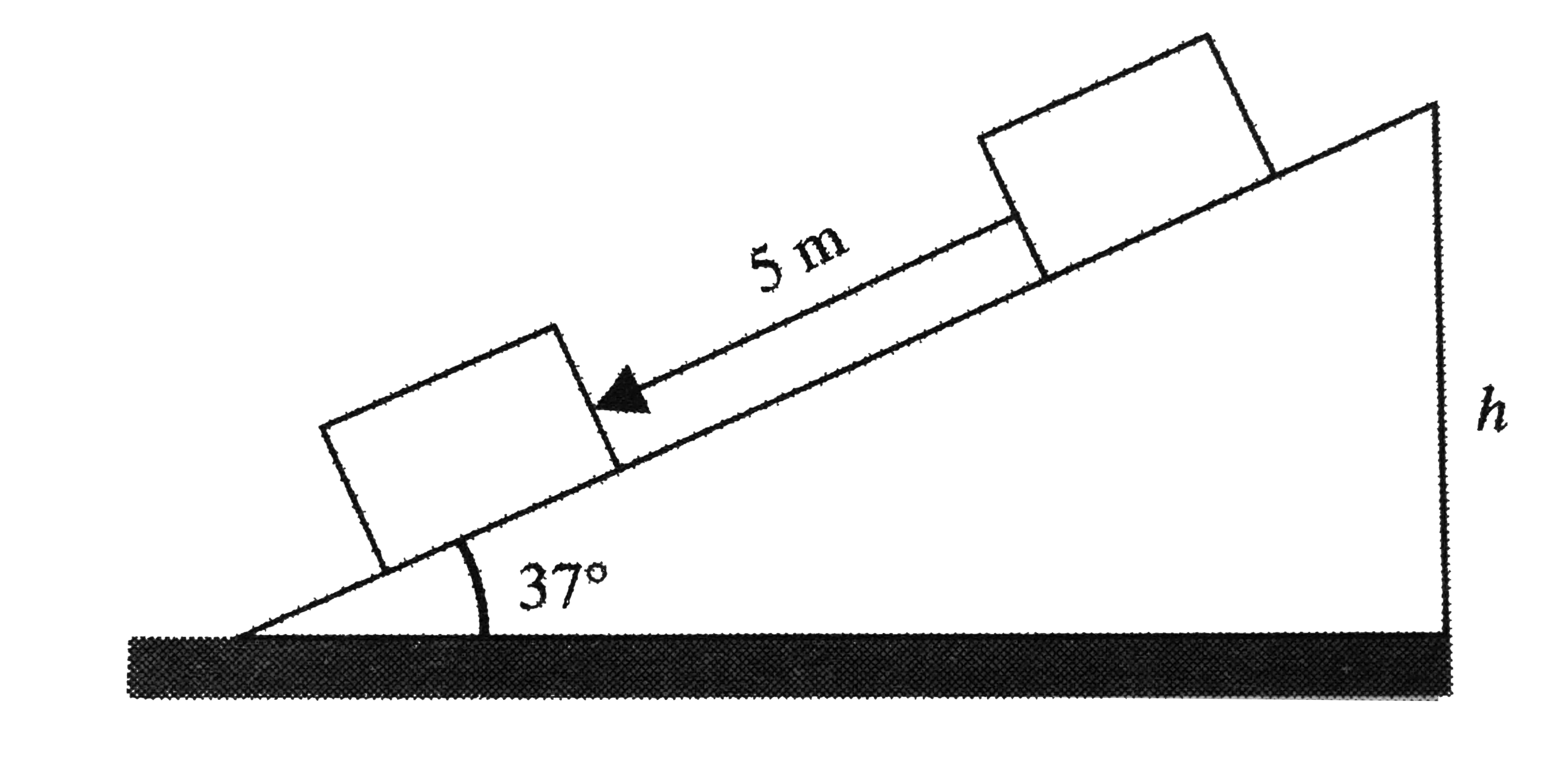
a. Find the speed of the block at the bottom if the inclined plane is smooth.
b. Find the speed of the block at the bottom if the coefficient of friction is 0.25.
View Solution
Knowledge Check
A block moves down a smooth inclined plane of inclination θ. Its velocity on reaching the bottom is v. If it slides down a rough inclined plane of some inclination, its velocity on reaching the bottom is v/n, where n is a number greater than 0. The coefficient of friction is given by -
Aμ=tanθ(1−1n2)Bμ=cotθ(1−1n2)Cμ=tanθ(1+1n2)Dμ=cotθ(1+1n2)A block moves down a smooth plane of inclination θ. Its velocity on reaching the bottom is v. If it slides down a rough inclined plane some inclination, its velocity on reaching the bottom is v/n, where n is a number greater than 0. The coefficient of friction is given by:
Aμ=tanθ(1−1n2)Bμ=cotθ(1−1n2)Cμ=tanθ(1−1n2)1/2Dμ=cotθ(1−1n2)1/2A block moves down a smooth inclined plane of inclination 45∘. Its velocity on reaching the bottom is v. If it slides down a rough inclined plane of same inclination, its velocity on reaching the bottom is vin, where n is a number greater than zero. The coefficient of friction μ is given by
Aμ=(1−1n)Bμ=(1−1n2)Cμ=√1−1n2Dμ=√1−1n
A block is placed on the top of a plane inclined at 37∘ with horizontal. The length of the plane is 5m. The block slides down the plane and reaches the bottom.

a. Find the speed of the block at the bottom if the inclined plane is smooth.
b. Find the speed of the block at the bottom if the coefficient of friction is 0.25.
View SolutionA particle starts from rest from the top of an inclined plane and again comes to rest on reaching the bottom most point of the inclined plane. If the coefficient of friction on some part of inclined plane is 3tanθ and rest portion is smooth then the ratio of the rough length of the inclined to smooth length is 1:n1 then value of n is .....?
View SolutionAn object is placed on the surface of a smooth inclined plane of inclination θ. It takes time t to reach the bottom. If the same object is allowed to slide down a rough inclined plane of inclination θ, it takes time nt to reach the bottom where n is a number greater than 1. The coefficient of friction μ is given by:-
View SolutionAn object is placed on the surface of a smooth inclined plane of inclination . It takes time t to reach the bottom of the inclined plane. If the same object is allowed to slide down rough inclined plane of same inclination , it takes time nt to reach the bottom where n is a number greater than 1. The coefficient of friction is given by -
View SolutionAn object is placed on the surface of a smooth inclined plane of inclination . It takes time t to reach the bottom of the inclined plane. If the same object is allowed to slide down rough inclined plane of same inclination , it takes time nt to reach the bottom where n is a number greater than 1. The coefficient of friction is given by -
View Solution
