In the above question, the ratio of masses of the charge particles q1,q2,andq3 is
1:1:1
q1:q2:q3
1:√3:2
This ratio cannot be calculated
The correct Answer is:C
To solve the problem regarding the ratio of masses of charged particles q1,q2, and q3, we can follow these steps:
Step 1: Understand the relationship between force, mass, and acceleration
According to Newton's second law, the force F acting on an object is equal to the mass m of the object multiplied by its acceleration a:
F=m⋅a
In circular motion, the centripetal force required to keep an object moving in a circle is given by:
F=mv2R
where v is the velocity of the object and R is the radius of the circular path.
Step 2: Set up the equations for each charged particle
Assuming that the charged particles q1,q2, and q3 are moving in circular paths under the influence of forces due to their charges, we can express the centripetal force for each particle:
- For particle q1:
F1=m1v21R1
- For particle q2:
F2=m2v22R2
- For particle q3:
F3=m3v23R3
Step 3: Relate the forces to the charges
The forces acting on the charged particles can also be expressed in terms of the charges and the electric field or other interactions. Assuming the forces are proportional to the charges, we can write:
F1∝q1,F2∝q2,F3∝q3
Step 4: Establish the ratios of the masses
From the proportionality of forces and the equations for centripetal force, we can derive the ratios of the masses:
m1v21R1:m2v22R2:m3v23R3
This leads to the conclusion that:
m1m2=q1v21/R1,m2m3=q2v22/R2,m3m1=q3v23/R3
Step 5: Solve for the specific ratio
If we assume specific values or relationships between the velocities and radii, we can simplify the ratios. The final result given in the video transcript states that:
m1:m2:m3=1:√3:2
Conclusion
Thus, the ratio of the masses of the charged particles q1,q2, and q3 is:
1:√3:2
According to Newton's second law, the force F acting on an object is equal to the mass m of the object multiplied by its acceleration a:
F=m⋅a
In circular motion, the centripetal force required to keep an object moving in a circle is given by:
F=mv2R
where v is the velocity of the object and R is the radius of the circular path.
Assuming that the charged particles q1,q2, and q3 are moving in circular paths under the influence of forces due to their charges, we can express the centripetal force for each particle:
- For particle q1:
F1=m1v21R1
- For particle q2:
F2=m2v22R2
- For particle q3:
F3=m3v23R3
The forces acting on the charged particles can also be expressed in terms of the charges and the electric field or other interactions. Assuming the forces are proportional to the charges, we can write:
F1∝q1,F2∝q2,F3∝q3
From the proportionality of forces and the equations for centripetal force, we can derive the ratios of the masses:
m1v21R1:m2v22R2:m3v23R3
This leads to the conclusion that:
m1m2=q1v21/R1,m2m3=q2v22/R2,m3m1=q3v23/R3
If we assume specific values or relationships between the velocities and radii, we can simplify the ratios. The final result given in the video transcript states that:
m1:m2:m3=1:√3:2
Thus, the ratio of the masses of the charged particles q1,q2, and q3 is:
1:√3:2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason Type8videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Comprehension Type94videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type2videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer12videos
MISCELLANEOUS VOLUME 5
Similar Questions
Three charged paricles are placed on a straight line as shown in fig. q1 and q2 are fixed but q3 can be moved. Under the action of the forces from q1,q2 and q3 is in equilbrium. What is the relation between q1 and q2.
 View Solution
View SolutionA charge particle q1, is at position (2, -1, 3). The electrostatic force on another charged particle q2 at (0, 0, 0) is :
View SolutionThree concentric metallic spherical shells of radii R, 2R, 3R are given charges Q1Q2Q3, respectively. It is found that the surface charge densities on the outer surface of the shells are equal. Then, the ratio of the charges given to the shells Q1:Q2:Q3 is
View SolutionIn the previous question,if the particle has−Q charge the time spend by the particle in the field will be .
View SolutionThree equal charges are placed on the three corners of a square. If the force between q1 and q2 is F12 and that between q1 and q3 is F13, then the ratio of magnitudes (F12/F13) is
View SolutionIdentify the correct statement about the charges q1 and q2 then
 View Solution
View SolutionA charge Q located at a point →r is in equilibrium under the combined field of three charges q1,q2 and q3. If the charges q1 and q2 are located at point →r1 and →r2 respectively, find the direction of the force on Q due to q3 in terms of q1,(q2),→r1→r2, and →r.
View SolutionA point charge q1 is placed inside cavity 1 and another point charge q2 is inside cavity 2. A point charge q is placed outside the conductor. For the situation described above, answer the following questions.
If the potential of the conductor is V0 and charge q2 is placed at the center of cavity 2, then potential at point Q isView SolutionIn the adjoining figure, the electric field lines for charges q1andq2 are shown. Identify the sign of the charges.
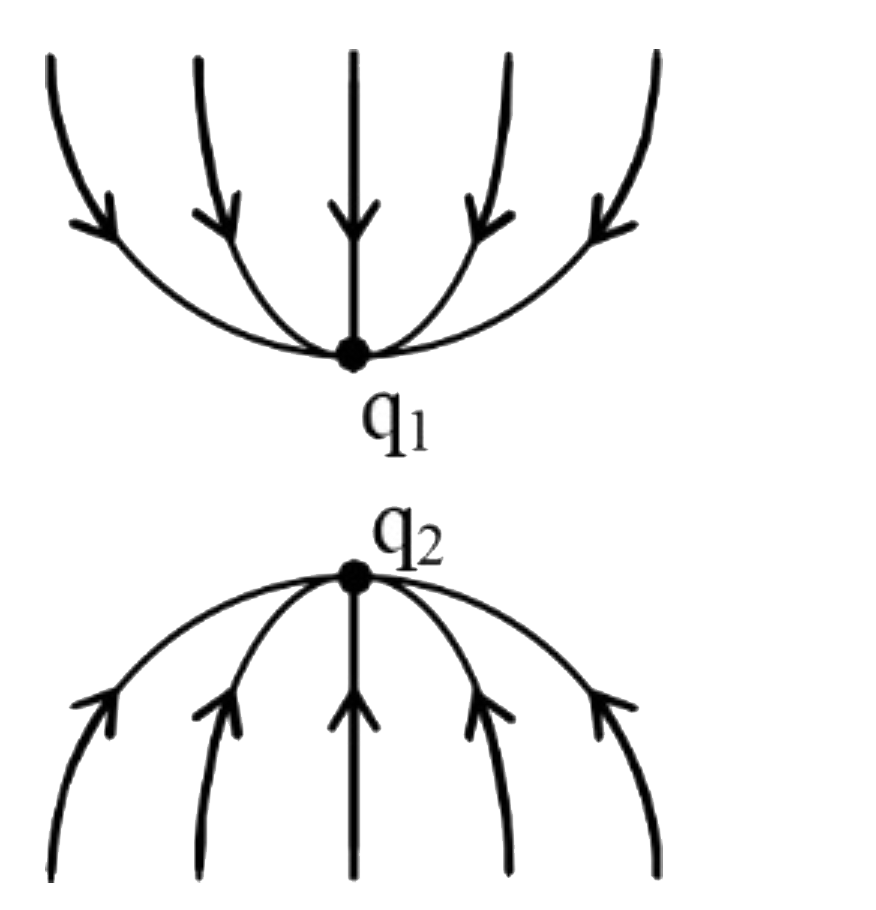 View Solution
View SolutionThe figure shows a region containing a uniform magnetic field B, which is increasing at the rate dBdt The region is gravity free. A disc of mass m and radius R is kept in this magnetic field. Two charged particles having charge q1andq2 and masses m and 2m are embedded to the non-conducting disc on the circumference at diametrically opposite points. The disc is free to translate as well as rotate.

If q1=−qandq2=q , then the initial acceleration of q1 will beView Solution
