A charge Q located at a point →r is in equilibrium under the combined field of three charges q1,q2 and q3. If the charges q1 and q2 are located at point →r1 and →r2 respectively, find the direction of the force on Q due to q3 in terms of q1,(q2),→r1→r2, and →r.
To solve the problem, we need to analyze the forces acting on the charge Q due to the other three charges q1,q2, and q3. Since the charge Q is in equilibrium, the net force acting on it must be zero. Let's break down the solution step by step.
Step 1: Understand the Forces Acting on Charge Q
The charge Q experiences forces due to charges q1, q2, and q3. We denote the forces as follows:
- →F1: Force on Q due to q1
- →F2: Force on Q due to q2
- →F3: Force on Q due to q3
Since Q is in equilibrium, we have:
→F1+→F2+→F3=0
Step 2: Express Forces →F1 and →F2
Using Coulomb's law, the forces can be expressed as:
→F1=kq1Q|→r−→r1|2^u1
→F2=kq2Q|→r−→r2|2^u2
where k is Coulomb's constant, ^u1 is the unit vector pointing from q1 to Q, and ^u2 is the unit vector pointing from q2 to Q.
Step 3: Find the Direction of →F3
From the equilibrium condition, we can express →F3:
→F3=−(→F1+→F2)
Substituting the expressions for →F1 and →F2:
→F3=−(kq1Q|→r−→r1|2^u1+kq2Q|→r−→r2|2^u2)
Step 4: Analyze the Resulting Direction
The direction of →F3 is opposite to the resultant of →F1 and →F2. Therefore, we can express the direction of →F3 in terms of the unit vectors ^u1 and ^u2:
^u3=−(q1^u1|→r−→r1|2+q2^u2|→r−→r2|2)
Final Expression for the Direction of →F3
Thus, the direction of the force on Q due to q3 can be summarized as:
^u3=−(q1(→r−→r1)|→r−→r1|3+q2(→r−→r2)|→r−→r2|3)
- →F1: Force on Q due to q1
- →F2: Force on Q due to q2
- →F3: Force on Q due to q3
→F1+→F2+→F3=0
→F1=kq1Q|→r−→r1|2^u1
→F2=kq2Q|→r−→r2|2^u2
where k is Coulomb's constant, ^u1 is the unit vector pointing from q1 to Q, and ^u2 is the unit vector pointing from q2 to Q.
→F3=−(→F1+→F2)
→F3=−(kq1Q|→r−→r1|2^u1+kq2Q|→r−→r2|2^u2)
^u3=−(q1^u1|→r−→r1|2+q2^u2|→r−→r2|2)
^u3=−(q1(→r−→r1)|→r−→r1|3+q2(→r−→r2)|→r−→r2|3)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Solved examples10videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Exercises58videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type51videos
CENGAGE PHYSICS DPP
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits15videos
ELECTRIC CURRENT & CIRCUITS
Similar Questions
In figure, the charges on C1,C2, and C3, are Q1,Q2, and Q3, respectively.
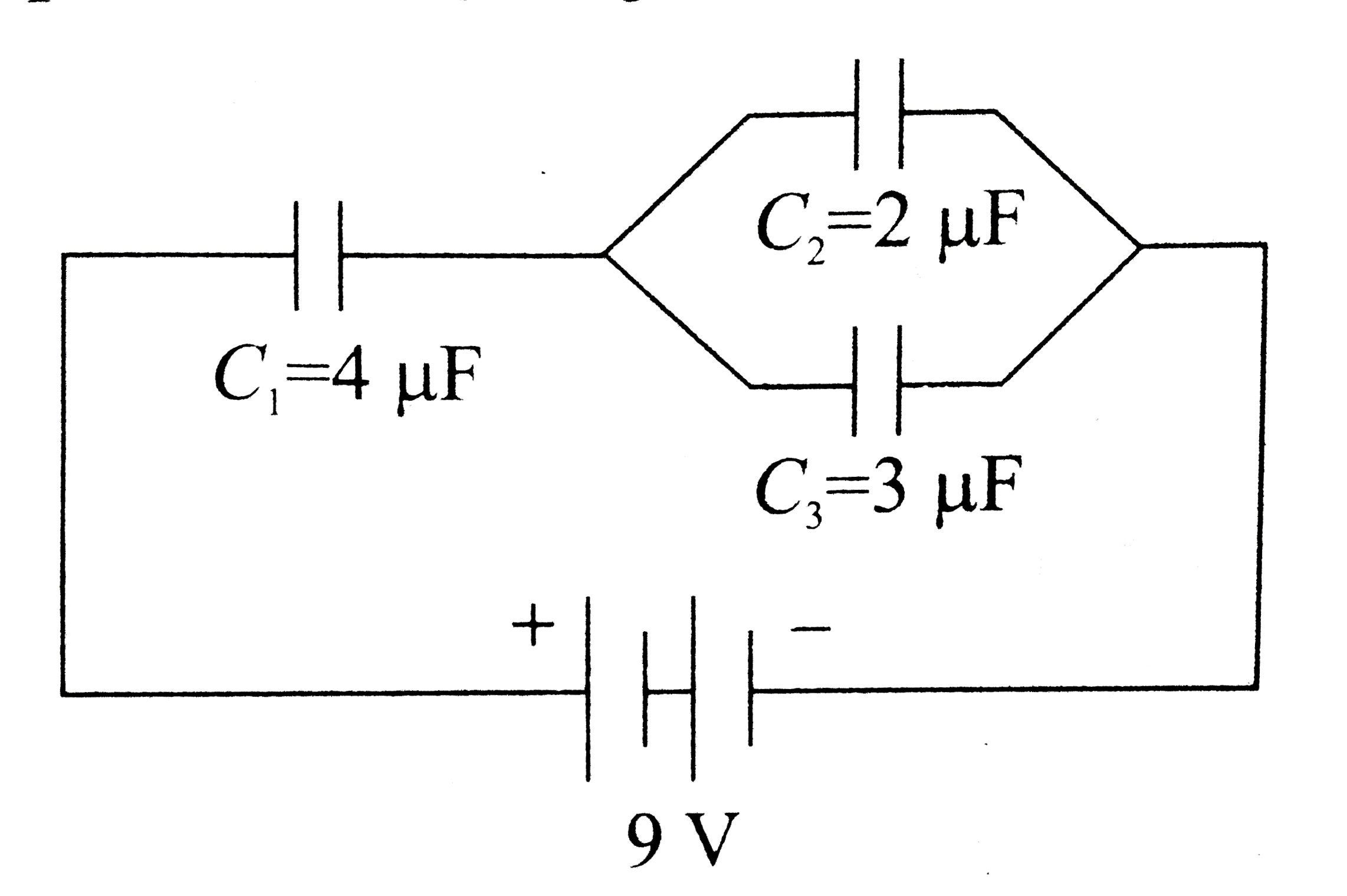 .View Solution
.View SolutionTwo point charges q1andq2 are located at →r1and→r2 respectively in an external electric field E. Obtain the expression for the total work done in assembling this configuration.
View SolutionThe insulated spheres of radii R1 and R2 having charges Q1 and Q2 respectively are connected to each other. There is
View SolutionThe insulated spheres of radii R1 and R2 having charges Q1 and Q2 respectively are connected to each other. There is
View SolutionFind out potential energy of the two point charge system having charges q1 and q2 separated by distance r.
View SolutionTwo metallic s pheres of radii R1 and R2 are connected b y a thin wire. If +q1~and+q_(2) are the charges on the two s pheres then
View SolutionTwo concentric spherical shells of radius R1 and R2(R2>R1) are having uniformly distributed charges Q1 and Q2 respectively. Find out total energy of the system.
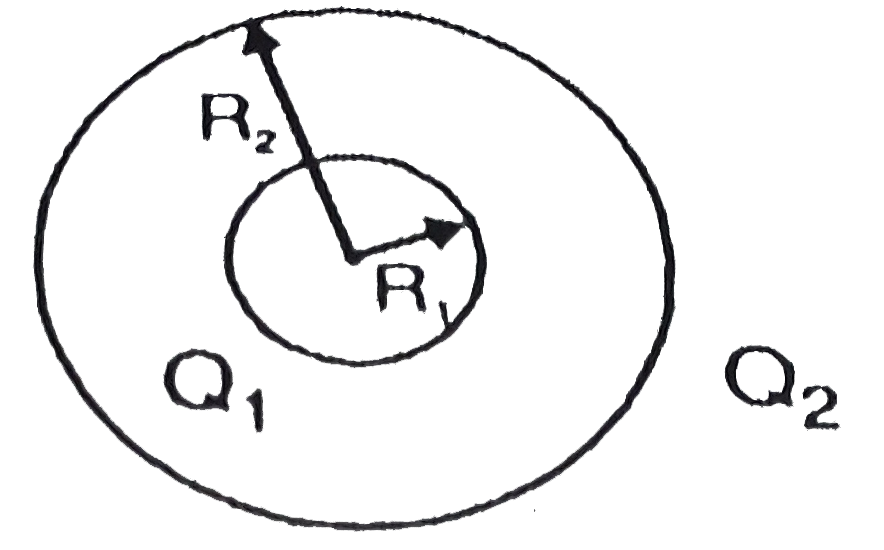 View Solution
View SolutionA positive point charge q1 is placed at (a,0) and another positive point charge q2 is placed at (0,a) . Find the force acting on q1.
View SolutionWhat is the direction of the force acting on a charged particle q, moving with a velocity →v a uniform magnetic field →B ?
View SolutionThree charged paricles are placed on a straight line as shown in fig. q1 and q2 are fixed but q3 can be moved. Under the action of the forces from q1,q2 and q3 is in equilbrium. What is the relation between q1 and q2.
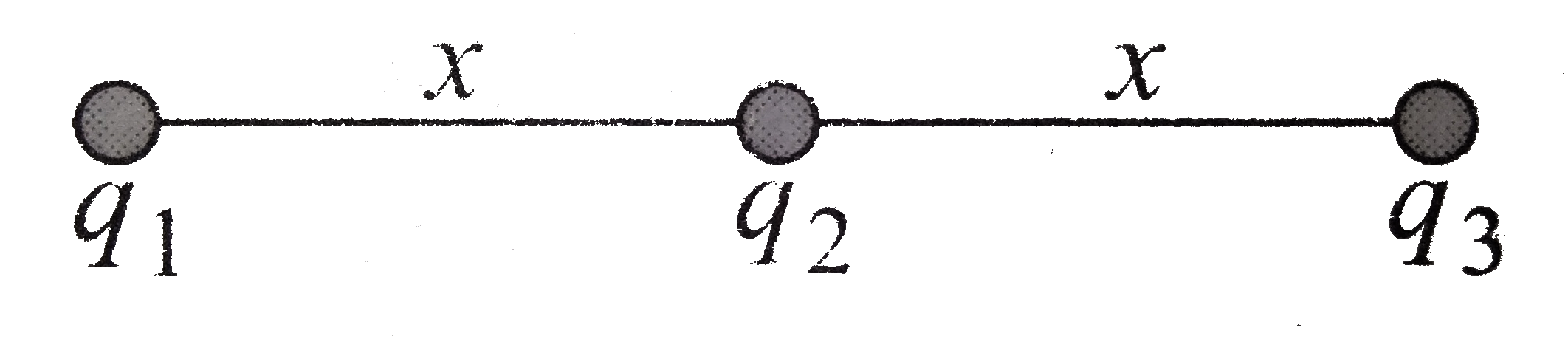 View Solution
View Solution

