In the arrangement shown in Fig., slits S1 and S4are having a variable separation Z. Point O on the screen is at the common perpendicular bisector of S1S2 and S3S4.
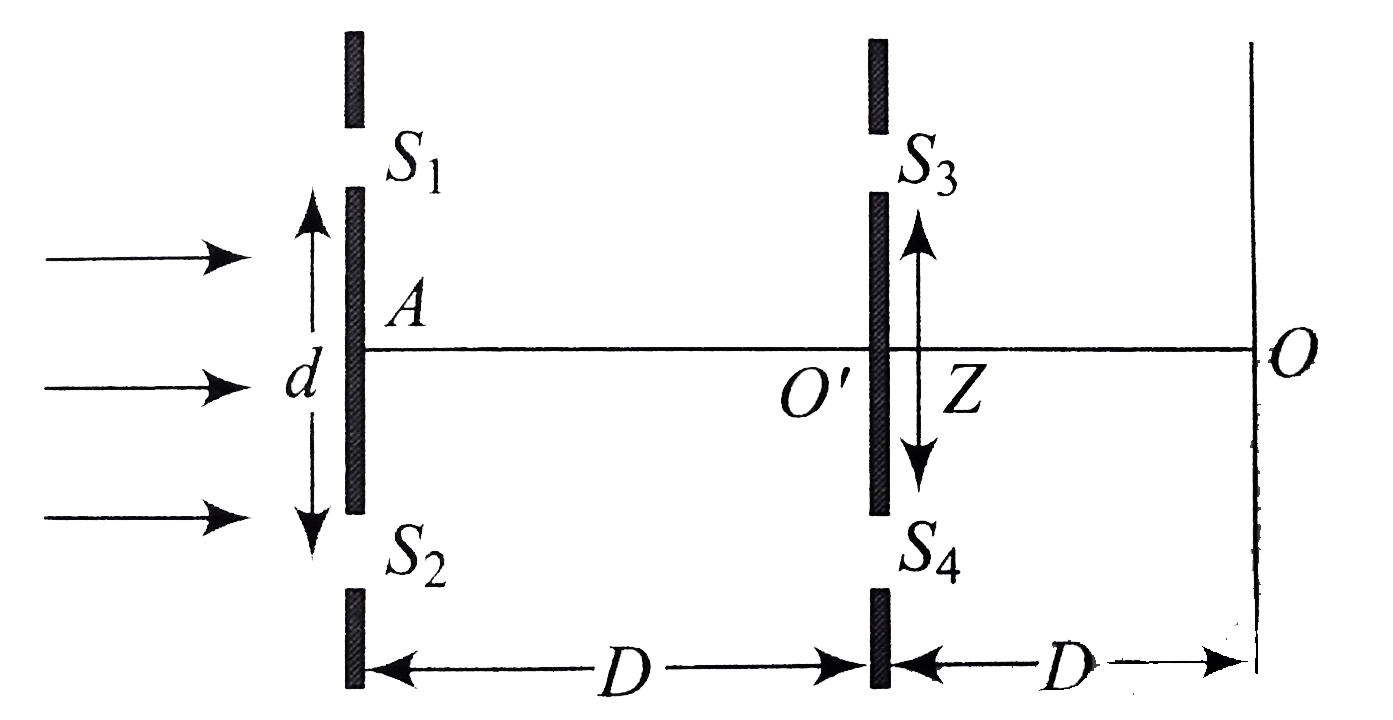
When Z=λD2d, the intensity measured at O is I0. The intensity at O When Z=2λDd is
I0
2I0
3I0
4I0
The correct Answer is:b
Intensity at O is proportional to intensity at S3 and at S4
I=kcos2(δ2), where k is constant and δ is the phase
difference.
δ=2πβ×Z2=πZβ, where β is fringe width
β=λDd
When Z=λD/2d:
δ=πdλD×λD2d=π2
I=I0=kcos2(π4)
k=2I0
When Z'=2λDd:
Path difference δ'=2πβZ'2=2πdλd×2πDλd=2π
Required intensity at O is
I'=kcos2.δ2=2I0cos2(π)=2I0
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Integer
3 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Archives
4 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - THERMODYNAMICSEXERCISE - QUESTION BANK
34 Videos
- WAVESBOOK - CENGAGE PHYSICSCHAPTER - WAVESEXERCISE - QUESTION BANK
38 Videos
Similar Questions
Parallel monochromatic beam is falling normally on two slits S1 and S2 separated by d as shown in figure. By some mechanism, the separation between the slits S3 and S4 can be changed. The intensity is measured at the point P which is at the common perpendicular bisector of S1S2 and S3S4. When z=Dλ2d, the intensity measured at P is I. and when z is equal to 4Dλd, Intensity is xl. Find x.

View SolutionConsider the arrangement shown in figure. By some mechanism,
the separation between the slits S3andS4 can be changed. The intensity is
measured at the point P which is at the common perpendicular bisector of S1S2
and S3S4. When z=Dλ2d, the intensity measured at P is I. Find the intensity when
z is equal to

(a)Dλd(b)3Dλ2d(c)2Dλd .
View Solution
Knowledge Check
In the arrangement shown in Fig., slits S1 and S4are having a variable separation Z. Point O on the screen is at the common perpendicular bisector of S1S2 and S3S4.
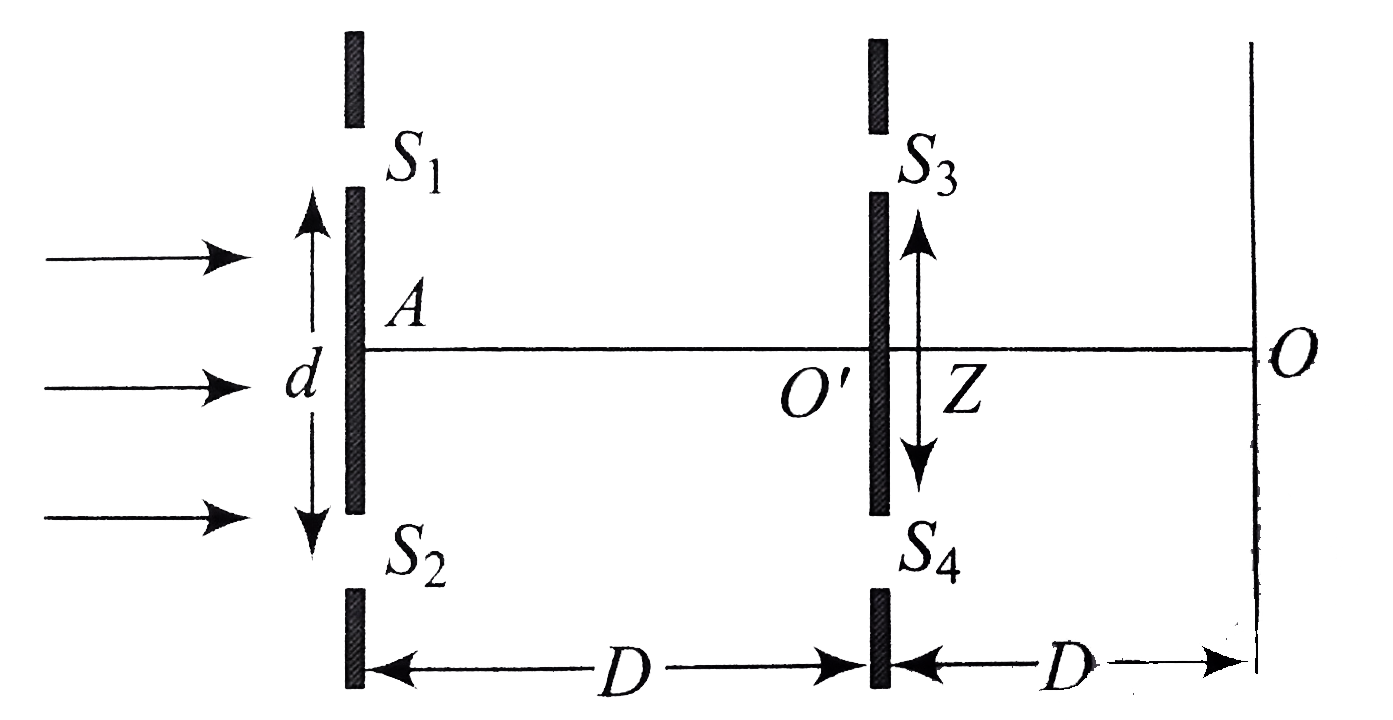
The minimum value of Z for which the intensity at O is zero isA2λDdBλD2dCλD3dDλDdIn the arrangement shown in Fig., slits S1 and S4are having a variable separation Z. Point O on the screen is at the common perpendicular bisector of S1S2 and S3S4.
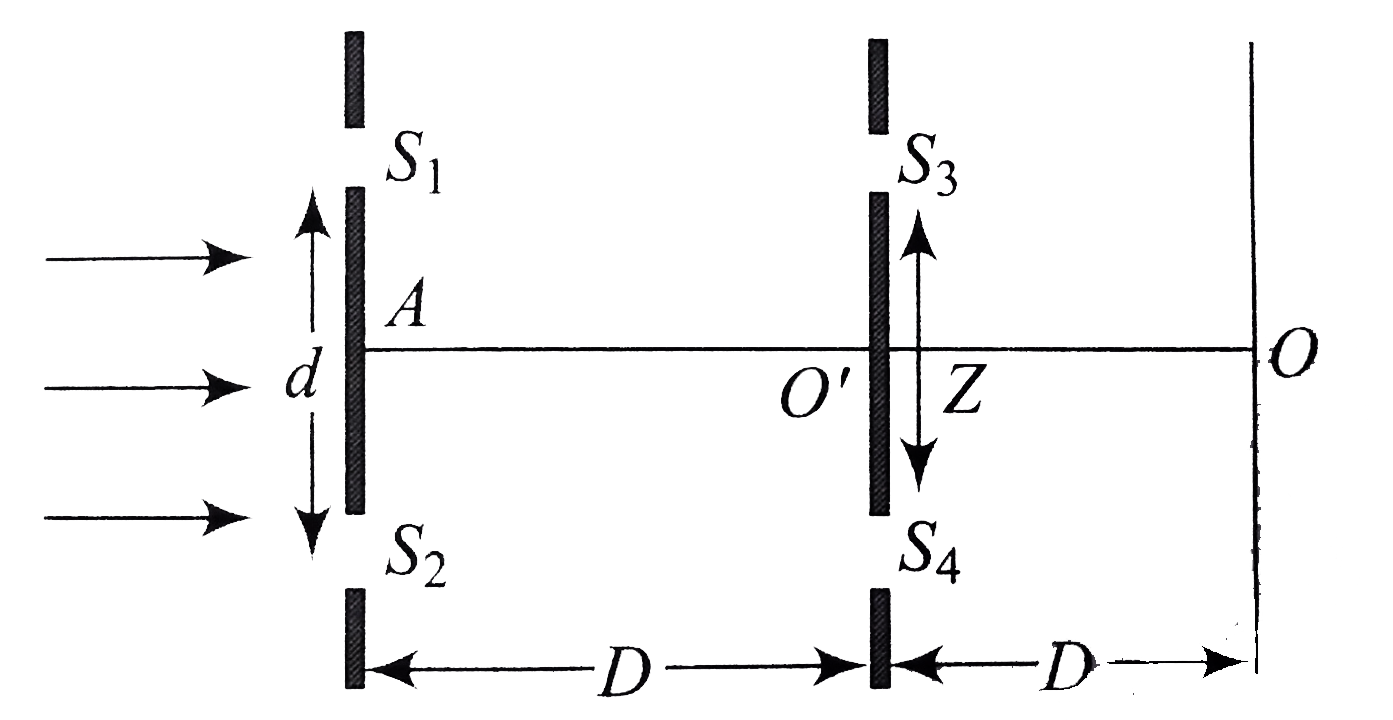
If a hole is made at O' on AO' O and the slit S4 is closed, then the ratio of the maximum to minimum observed on screen at O , if O'S3 is equal to λD4d, isA1BinfinityC34D4In arrangement shown in figure, plane wavefront of monochromatic light of wavelength λ is incident on identical slits S1 and S2. There is another pair of indentical slits S3 and S4 which are having separation Z=λD2d Point O is on the screen at the common perpendicular bisector of S1S2 and S3S4.I1 is the intensity at point O Now the board having slits S3S4 is moved upward parallel to itself and perpendicular to line AO till slit S4 is on line AO and it is observed that now intensity at point O is I2 then I2I1 is :
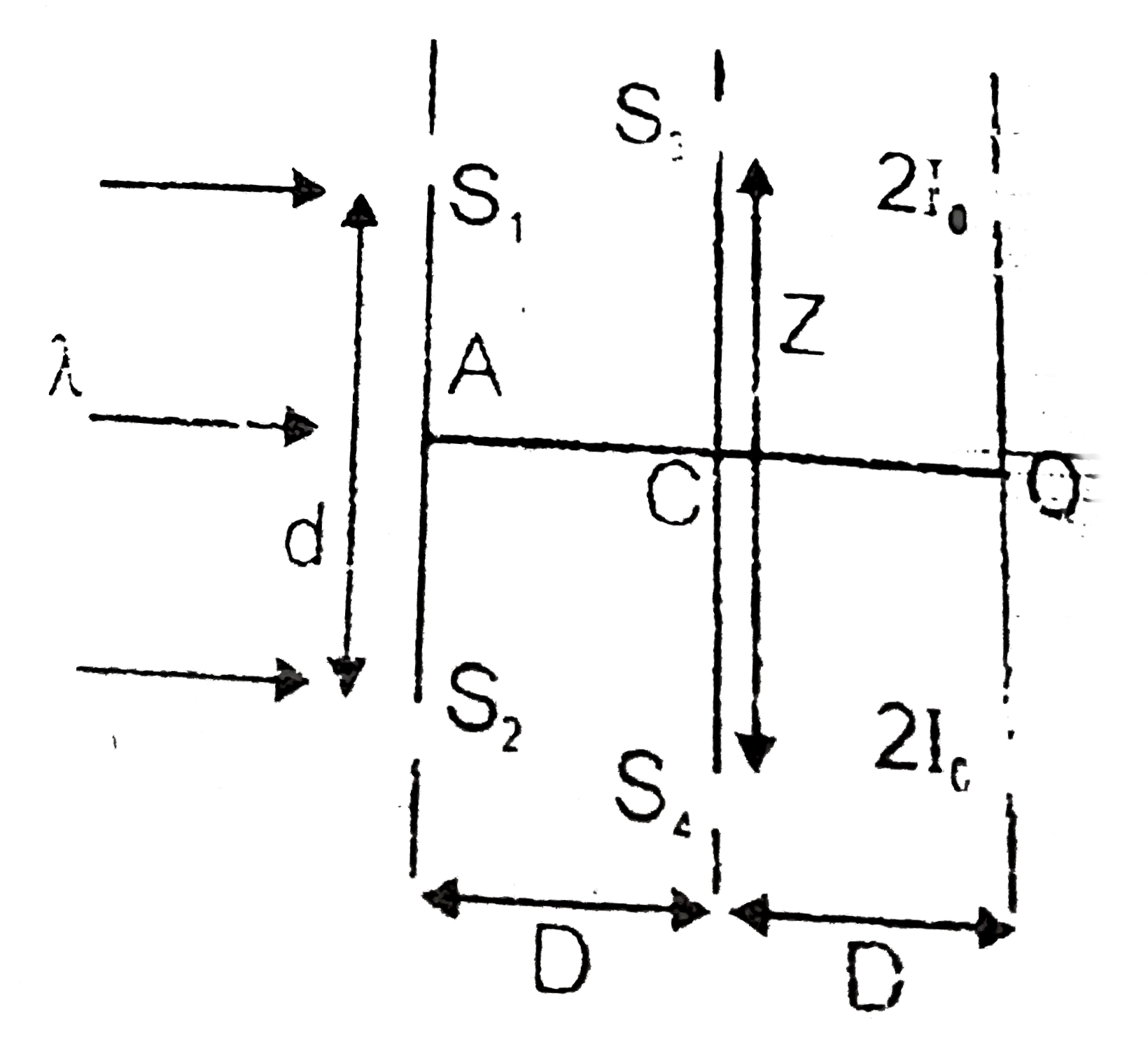 A12B2C1D0
A12B2C1D0
Consider the arrangement shownin figure. By some mechanism,the separation between the slits S3andS4 can be changed. The intensity in measured at the point P which is at the common perpendicular bisector of S1S2andS3S4.Whenz=(Dlamda)/(2d)the∫ensitymeasuredatPisI.F∈dthis∫ensitywhenzisequal→<br>a.Dλd,b.3Dλ2d,c.2Dλd

View SolutionIn the figure shown S1O−S2O=S3O−S2O=λ4, Intensity at O due to any one of the slits is I0. What is the intensity due to all the three coherent sources S1,S2andS3 ?
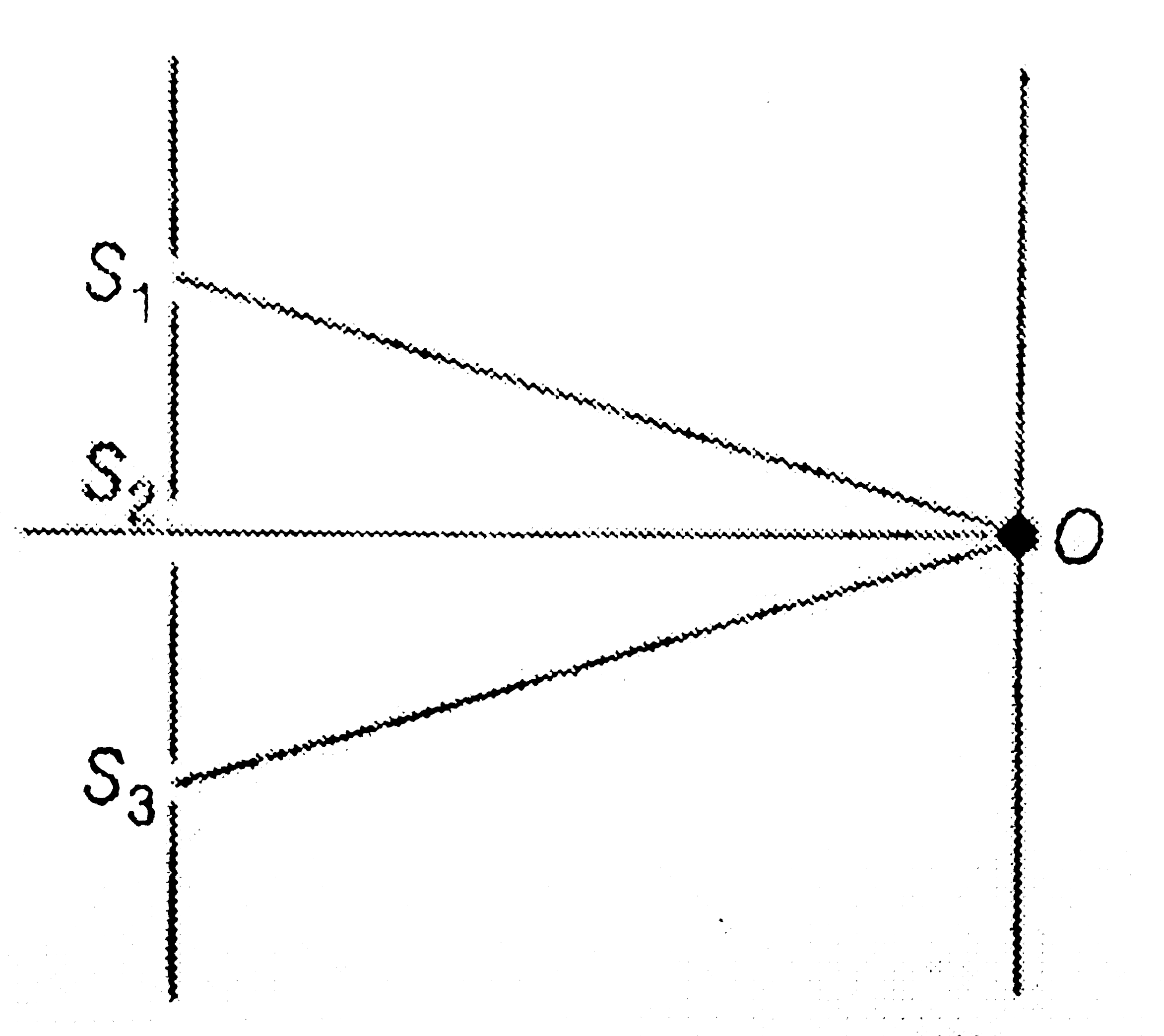
View Solution_E01_054_Q01.png)
A monochromatic light source of wavelength λ is placed at S. three slits S1,S2 and S3 are equidistant from the source S and the point P on the screen S1P−S2P=λ/6 and S1P−S3P=2λ/3. if I be the intensity at P when only one slit is open the intensity at P when all the three slits are open is-
View SolutionTwo coherent point sources S1andS2 are separated by a small distance 'd' as shown. The fringes obtained on the screen will be :

View SolutionTwo coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be

View Solution
