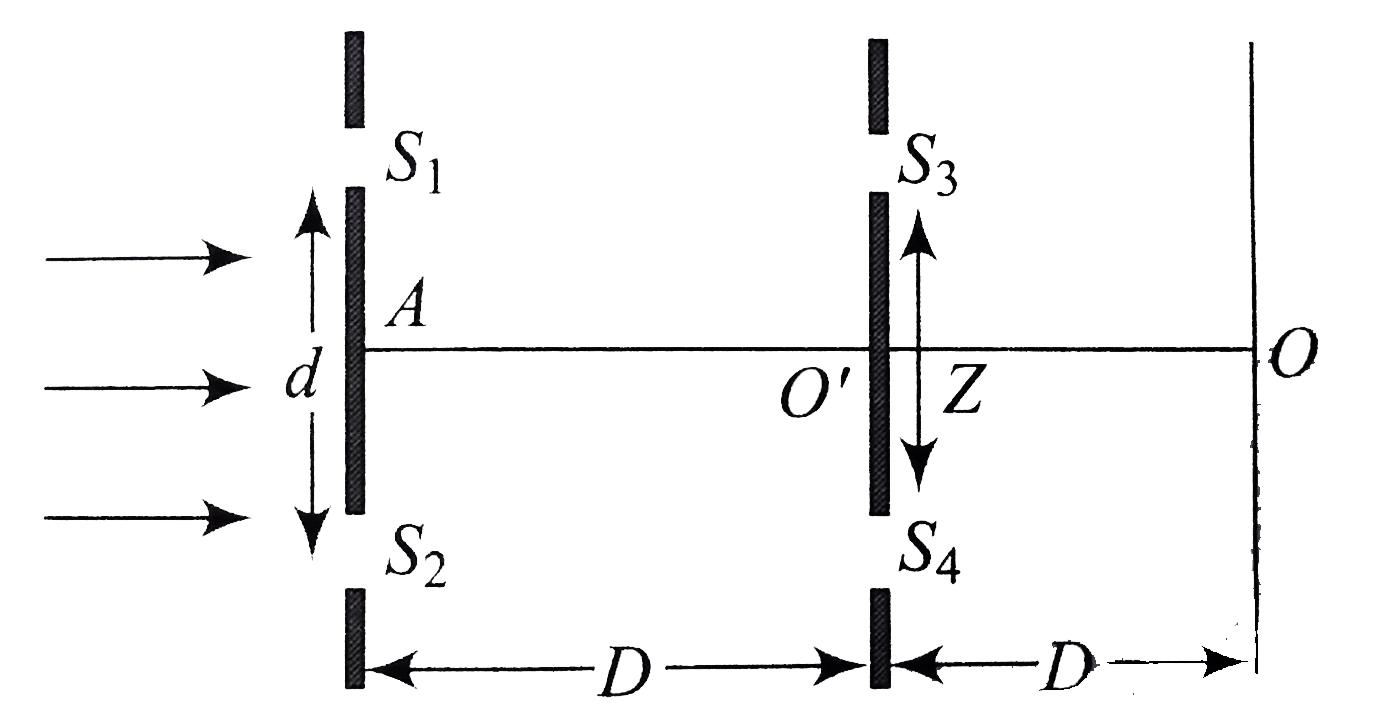
Consider the arrangement shownin figure. By some mechanism,the separation between the slits $S_{3} and S_{4}$ can be changed. The intensity in measured at the point P which is at the common perpendicular bisector of $S_{1} S_{2} and S_{3} S_{4} . W h e n$ z=(Dlamda)/(2d) $t h e \int e n s i t y m e a s u r e d a t P i s I . F \in d t h i s \int e n s i t y w h e n z i s e q u a l \to < b r > a . \frac{D λ}{d}, b . \frac{3 D λ}{2 d}, c . \frac{2 D λ}{d}$

Text Solution

Verified by Experts

The correct Answer is:A, B, C

a. When $z = \frac{λ D}{d}$
So, $O S_{3} = O S_{4} = \frac{λ D}{d}$
$\to D a r k \in \geq a t$ S_3 and S_4 $< b r >$ rarr At S_3 $\int e n s i t y a t$ S_3=0 $< b r >$ rarrl_1=0 $< b r > A t$ S_4 Intensity at S_4=0 $< b r >$ rarr $l_{2} = 0$
$\to A t P p a t h d \Leftrightarrow e r e n c e = 0 < b r >$ rarr Phase difference =0 $< b r >$ rarr l=l_1+l_2+2sqrt(l_1l_2)costheta^@=0+0+0=0 $< b r >$ rarr intensilty at P=0

Updated on:21/07/2023

|

Class 12 PHYSICS GEOMETRICAL OPTICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

In the arrangement shown in Fig., slits $S_{1}$ and $S_{4}$ are having a variable separation Z. Point O on the screen is at the common perpendicular bisector of $S_{1} S_{2}$ and $S_{3} S_{4}$ .

When $Z = \frac{λ D}{2 d}$ , the intensity measured at O is $I_{0}$ . The intensity at O When $Z = \frac{2 λ D}{d}$ is
A $I_{0}$
B $2 I_{0}$
C $3 I_{0}$
D $4 I_{0}$
In the arrangement shown in Fig., slits $S_{1}$ and $S_{4}$ are having a variable separation Z. Point O on the screen is at the common perpendicular bisector of $S_{1} S_{2}$ and $S_{3} S_{4}$ .

The minimum value of Z for which the intensity at O is zero is
A $\frac{2 λ D}{d}$
B $\frac{λ D}{2 d}$
C $\frac{λ D}{3 d}$
D $\frac{λ D}{d}$
In the arrangement shown in Fig., slits $S_{1}$ and $S_{4}$ are having a variable separation Z. Point O on the screen is at the common perpendicular bisector of $S_{1} S_{2}$ and $S_{3} S_{4}$ .

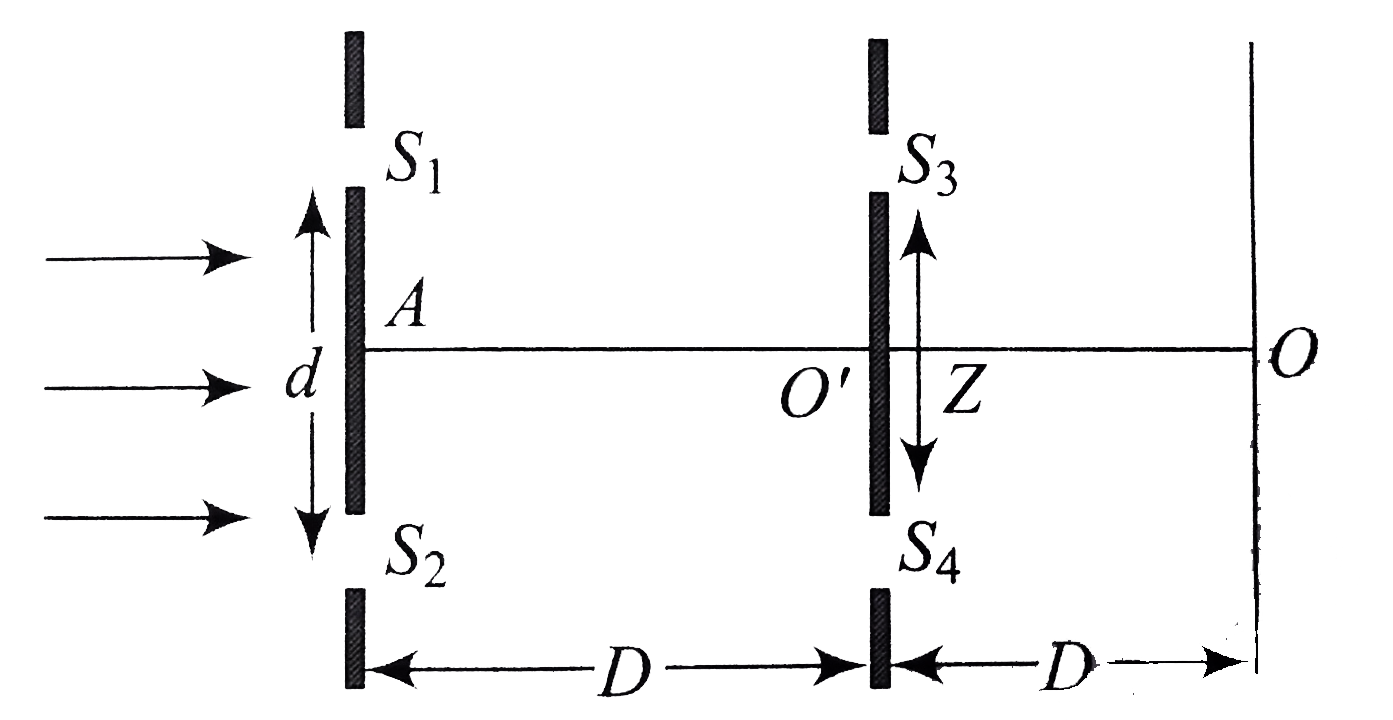
If a hole is made at O' on AO' O and the slit $S_{4}$ is closed, then the ratio of the maximum to minimum observed on screen at O , if $O' S_{3}$ is equal to $\frac{λ D}{4 d}$ , is
A1
Binfinity
C34
D4

HC VERMA-LIGHT WAVES-Exercises

Home
Ask Doubt
Profile