In the arrangement shown in figure the masses m of the bar and M of the wedge, as well as the wedge angle α, are known. The masses of the pulley and the thread are negligible. The friction is absent. Find the acceleration of the wedge M.
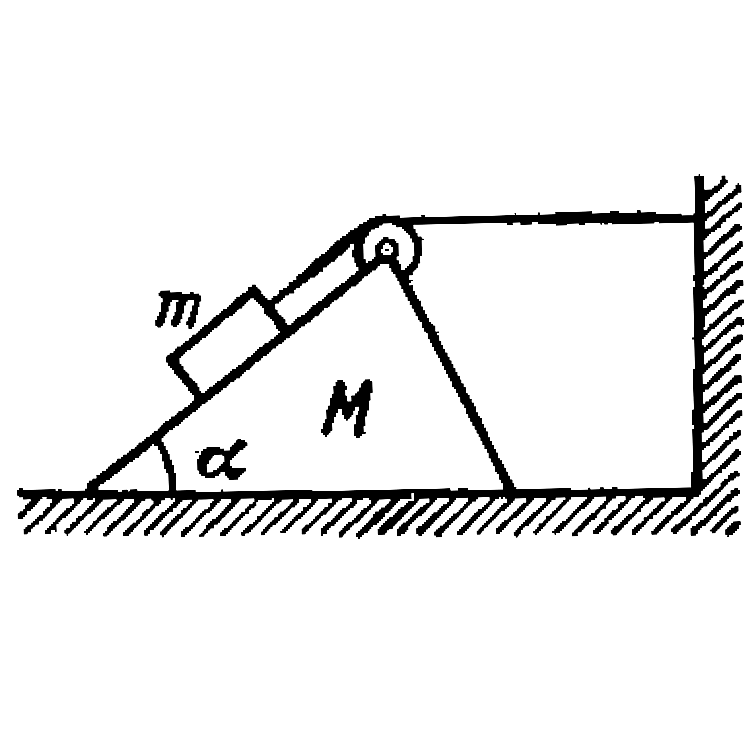
To analyse the kinematic relations between the bodies, sketch the force diagram of each body as shown in the figure.
On the basis of force diagram, it is obvious that the wedge M will move towards right and the block will move down along the wedge. As the length of the thread is constant, the distance travelled by the block on the wedge must be equal to the distance travelled by the wedge on the floor. Hence dsmM=dsM. As →vmM and →vM do not change their directions and acceleration that's why →wmM↑↑→vmM and →wM↑↑→vM and wmM=wM=w (say) and according the diagram of kinematical dependence is shown in figure.


As →wm=→wmM+→wM, so from traingle law of vector addition.
wm=√w2M+w2mM−2wmMwMcosα=w√2(1−cosα) (1)
From Fx=mwx, (for the wedge),
T=Tcosα+Nsinα=Mw (2)
For the bar m let us fix (x-y) coordinate system in the frame of ground Newton's law in projection form along x and y axes (figure) gives
mgsinα−T=mwm(x)=m[wmM(x)+wM(x)]
=m[wmM+wMcos(π−α)]=mw(1−cosα] (3)
mgcosα−N=mwm(y)=m[wmM(y)+wM(y)]=m[0+wsinα] (4)
Solving the above Eqs. simultaneously, we get
w=mgsinαM+2m(1−cosα)
Note: We can study the motion of the block m in the frame of wedge also, alternately we may solve this problem using conservation of mechanical energy.
Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Laws Of Conservation Of Energy, Momentum And Angular Momentum
82 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Universal Gravitation
34 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena
38 Videos
Similar Questions
In the arrangement shown in figure-2.68 the masses of the wedge M and the body m are known. There is no friction at any of the surfaces. The mass of the pulleys and thread is negligible. Find the acceleration of the body m relative to the horizontal surface on which the wedge slides.
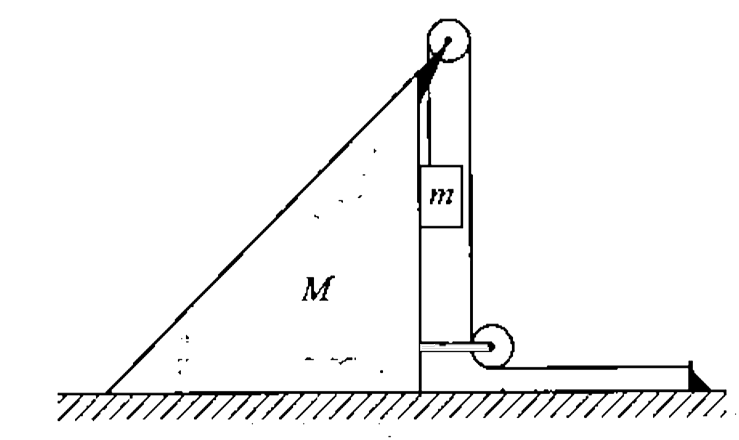
[√2mgM+2m]
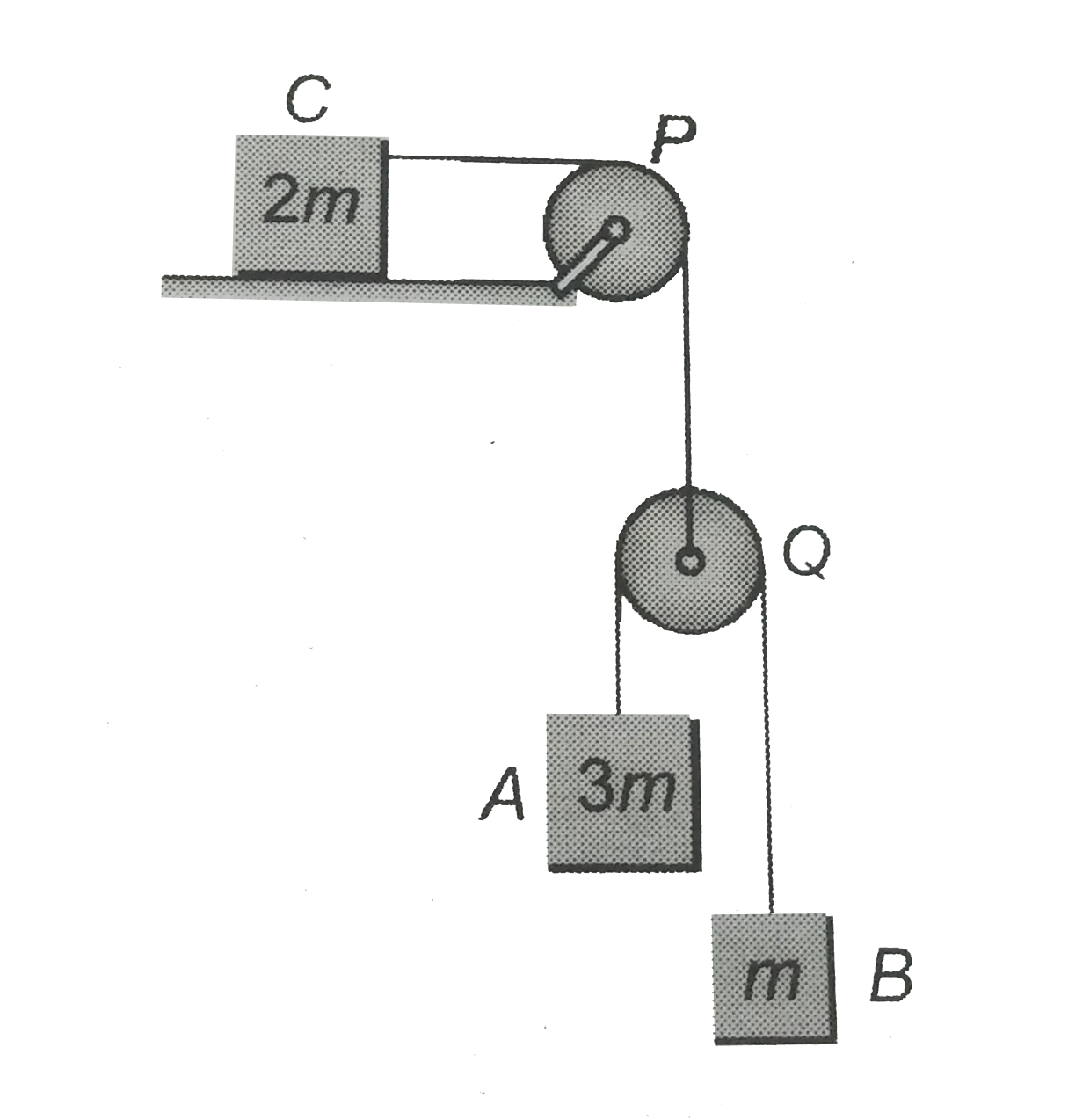
View SolutionIn the arrangement shown in the figure, the blocks have masses 3m,m and 2m, the friction is absent, the masses of the pulleys and the threads are negligible. Find the acceleration of mass 3m.
View Solution
Knowledge Check
In fig. mass m is being pulled on the incline of a wedge of mass M. All the surfaces are smooth. Find the acceleration of the wedge.
 Aa=F(1−cosθ)mg2sinθcosθM+2msin2θBa=F(1+cosθ)+mgsinθcosθM+msin2θCa=F(1−cosθ)−mgsinθcosθM+msin2θDa=F(1+cosθ)−mgsinθcosθM−msin2θ
Aa=F(1−cosθ)mg2sinθcosθM+2msin2θBa=F(1+cosθ)+mgsinθcosθM+msin2θCa=F(1−cosθ)−mgsinθcosθM+msin2θDa=F(1+cosθ)−mgsinθcosθM−msin2θ
A pulley fixed to the ceiling carries a thread with bodies of masses m1 and m2 attached to its ends. The masses of the pulley and the thread are negligible, friction is absent. Find the acceleration wC of the centre of inertia of this system.
View SolutionA pulley fixed to the ceiling carried a thread with bodies of masses m1 and m2 attached to its ends. The mases of the pulley and the thread are negligible and friction is absent. Find the acceleration of the centre of mass of this system.
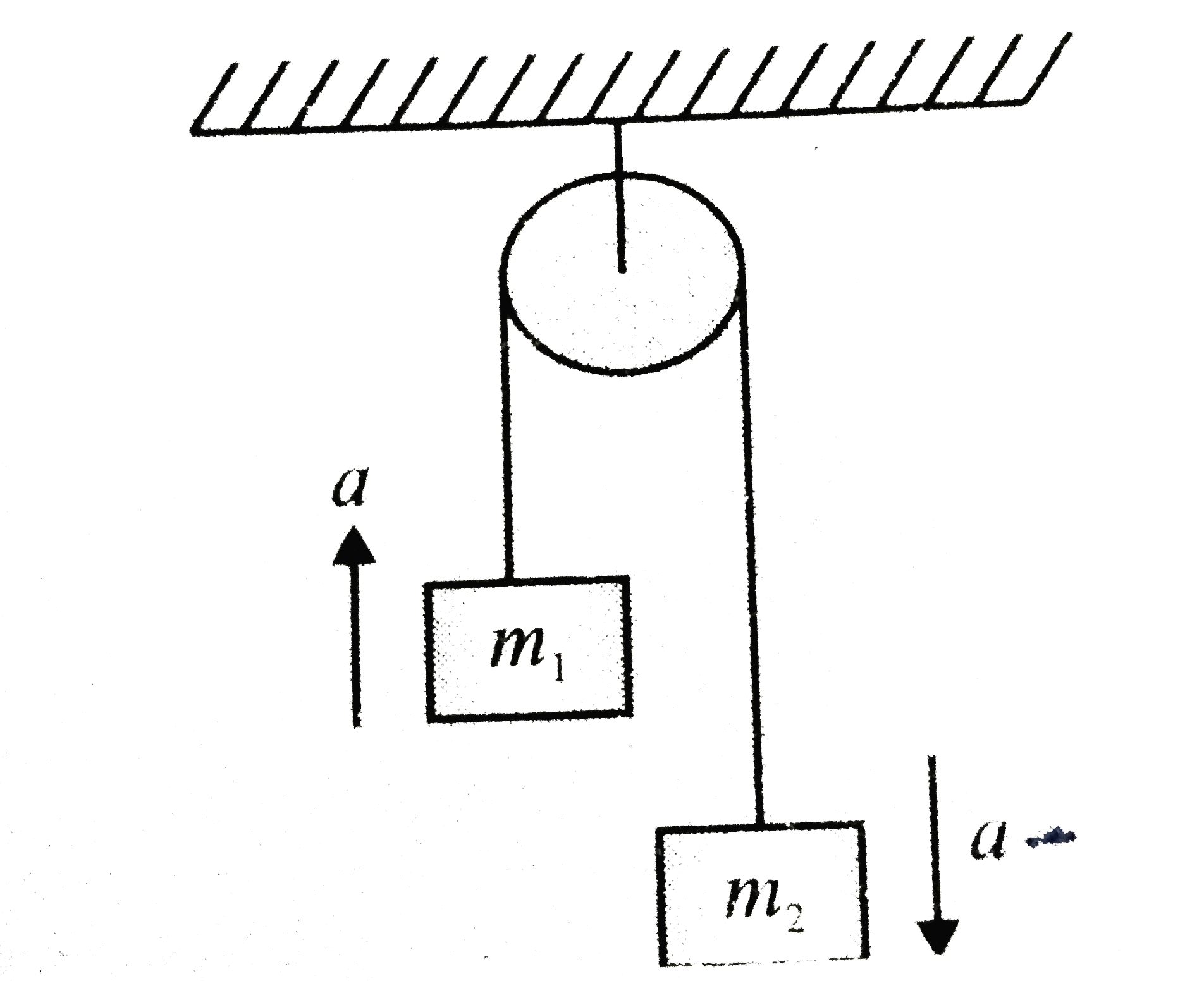
View SolutionIn the arrangement shown in figure the bodies have masses m0, m1, m2, the friction is absent, the masses of the pulleys and the threads are negligible. Find the acceleration of the body m1. Look into possible cases.

View SolutionIn the arrangement shown in figure the masses of the wedge M and the body m are known. The appreciable friction exists only between the wedge and the body m, the friction coefficient being equal to k. The masses of the pulley and the thread are negligible. Find the acceleration of the body m relative to the horizontal surface on which the wedge slides.

View SolutionIn the arrangement shown in fig the bodies have masses m0,m1andm2 the friction is absent the masses of pulleys and the threads are negligible find the acceleration of the body m1

View SolutionA pulley fixed to the ceiling carries a thread with bodies of masses m1 and m2 attached at its ends. The masses of the pulley and thread are negligible, friction is absent. Find the acceleration of the centre of mass(acm) of this system.
View SolutionIn the arrangement shown in figure, the rod of mass m held by two smooth walls, remains always perpendicular to the surface of the wedge of mass M. Assuming all the surface to be frictionless, find the acceleration of the rod and that of the wedge.

View Solution
