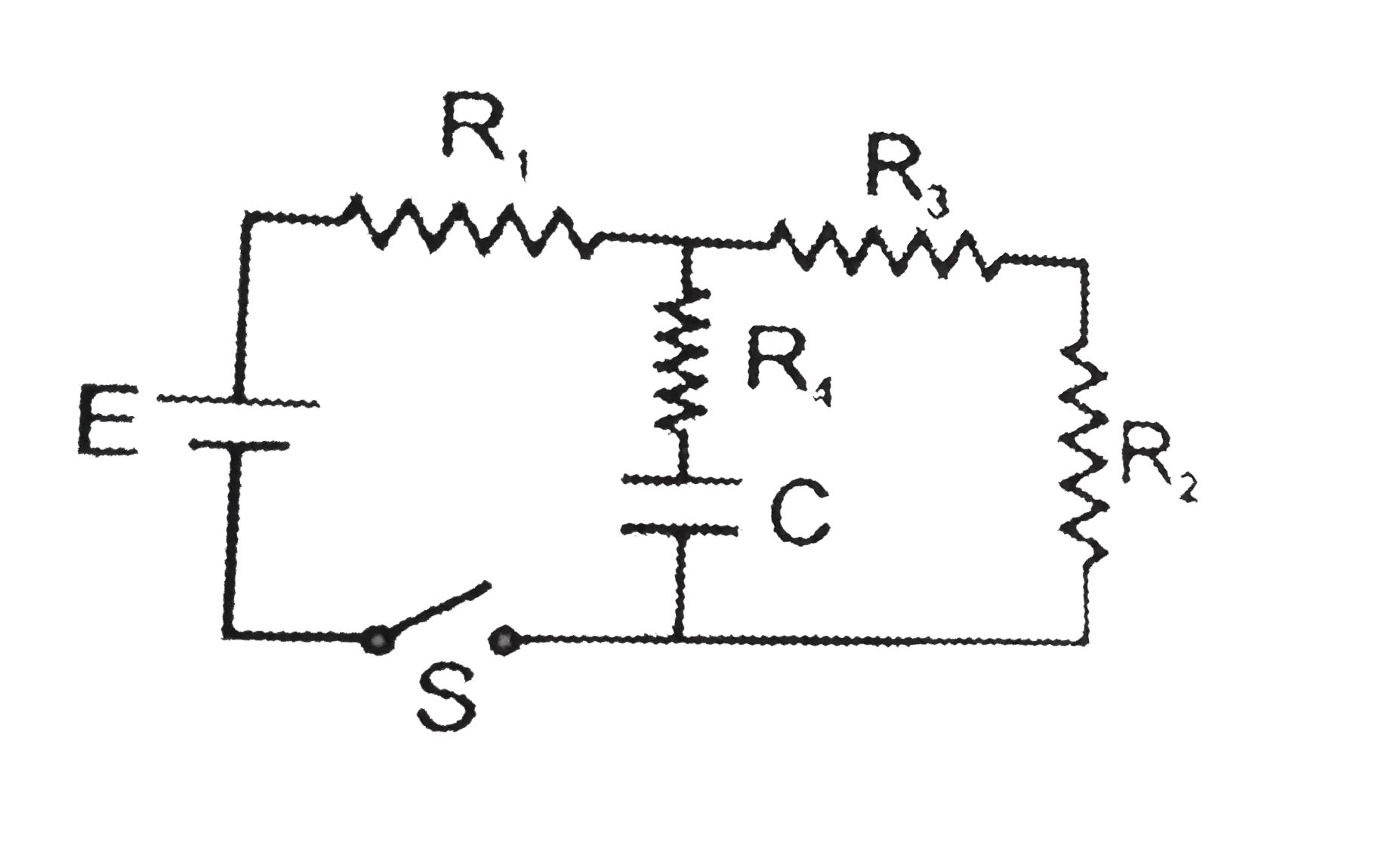
In the circuit shown in Figure, switch S1 is kept closed and S2 open for a long time. Resistance R1=1000R and R2=10−3R.
(a) Switch S1 is opened at time t = 0. Write the current and potential drop across R1 immediately after S1 is opened. What will be value of current after a long time?
(b) Switch S2 is closed (S1 is already closed since long) at time t = 0. Write current and potential drop across R2 immediately after this operation. Write current through the inductor as a function of time.
Text Solution
The correct Answer is:(a) Current =ER,VR1=1000E,I∞=E1001R≅10−3ER
(b) AT t=0+:i0=ER,VR2=10−3E,
i=1000ER[1−e−Rt1000L]
|
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - ARIHANTCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 3
12 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - ARIHANTCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 3
12 Videos
- CURRENT ELECTRICITYBOOK - ARIHANTCHAPTER - CURRENT ELECTRICITYEXERCISE - Current Electricity
105 Videos
- ELECTROSTATICSBOOK - ARIHANTCHAPTER - ELECTROSTATICSEXERCISE - Level 3
59 Videos
Similar Questions
Knowledge Check
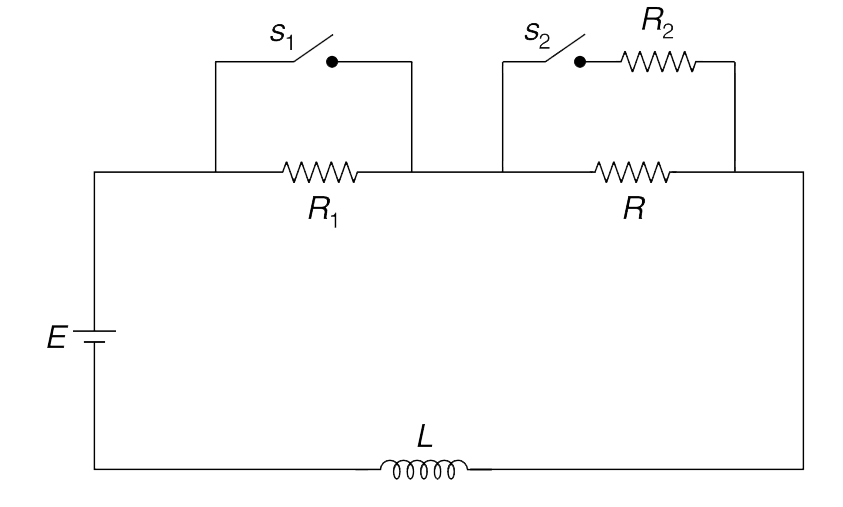
In the circuit shown in the figure, if switches S1 and S2 have been closed for a long time, then charge on the capacitor.
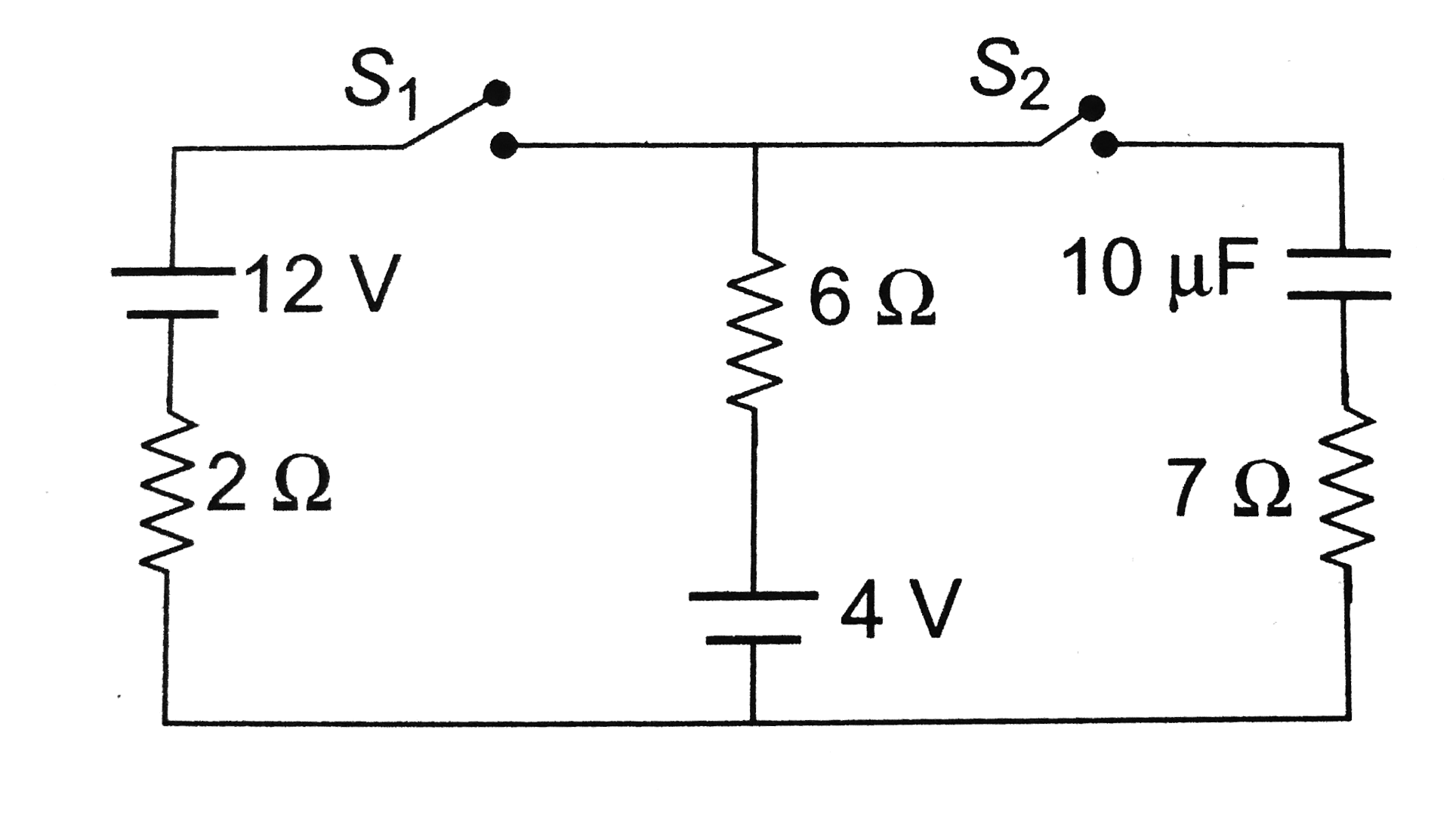 Ais 100μCBincreases to 200μC if one third of the gap of the capacitor's plates is filled with a dielectric (K=2) of same areaCboth (a) and (b) aboveDcharge on the capacitor remains unchanged if one third of the gap of the capacitor's plates is filled with a dielectric (K=2) of same area.
Ais 100μCBincreases to 200μC if one third of the gap of the capacitor's plates is filled with a dielectric (K=2) of same areaCboth (a) and (b) aboveDcharge on the capacitor remains unchanged if one third of the gap of the capacitor's plates is filled with a dielectric (K=2) of same area.After switch S2 is closed and S1 is opened, the maximum value of current through the inductor is:
A(√CL)EB(√C2L)EC(√3C2L)ED(√5C4L)EIn the circuit shows (Fig.) switches S1 and S3 have been closed for 1s and S2 remained open. Just after 1s, switch S2 is closed and S1 and S3 are opened. Find after that instant (t=0):
the maximum charge on the capacitorA√3(1+1e)B√3(1−1e)C√2(1+1e)D√2(1−1e)
In the circuit diagram shown in the figure the switches S1 and S2 are closed at time t=0.After time t=(0.1)ln2sec, switch S2 is opened.The current in the circuit at time t=0.2n2sec is equal to x32amp.Find out value of x.
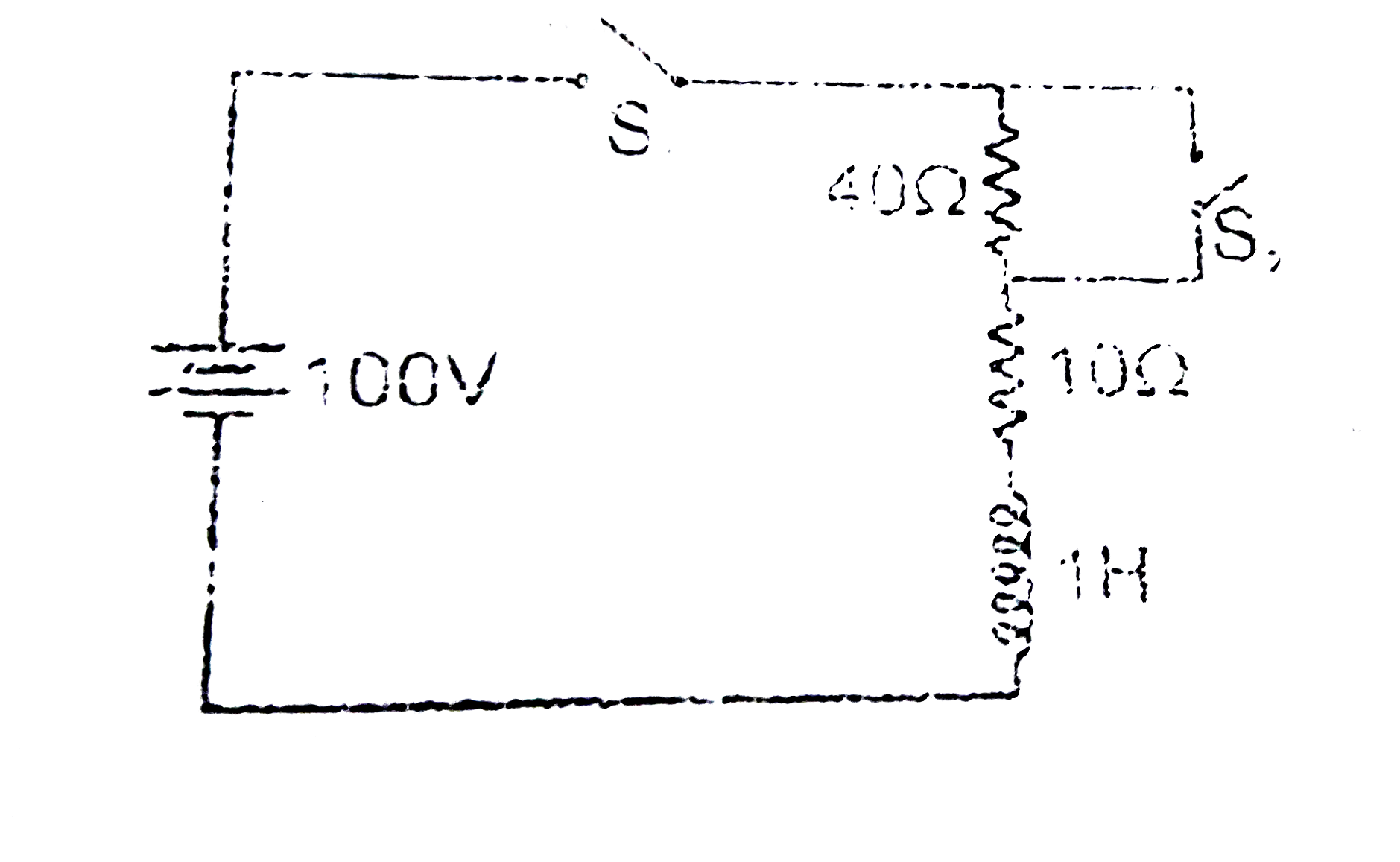
View SolutionIn the circuit shows (Fig.) switches S1 and S3 have been closed for 1s and S2 remained open. Just after 1s, switch S2 is closed and S1 and S3 are opened. Find after that instant (t=0):

the maximum charge on the capacitor
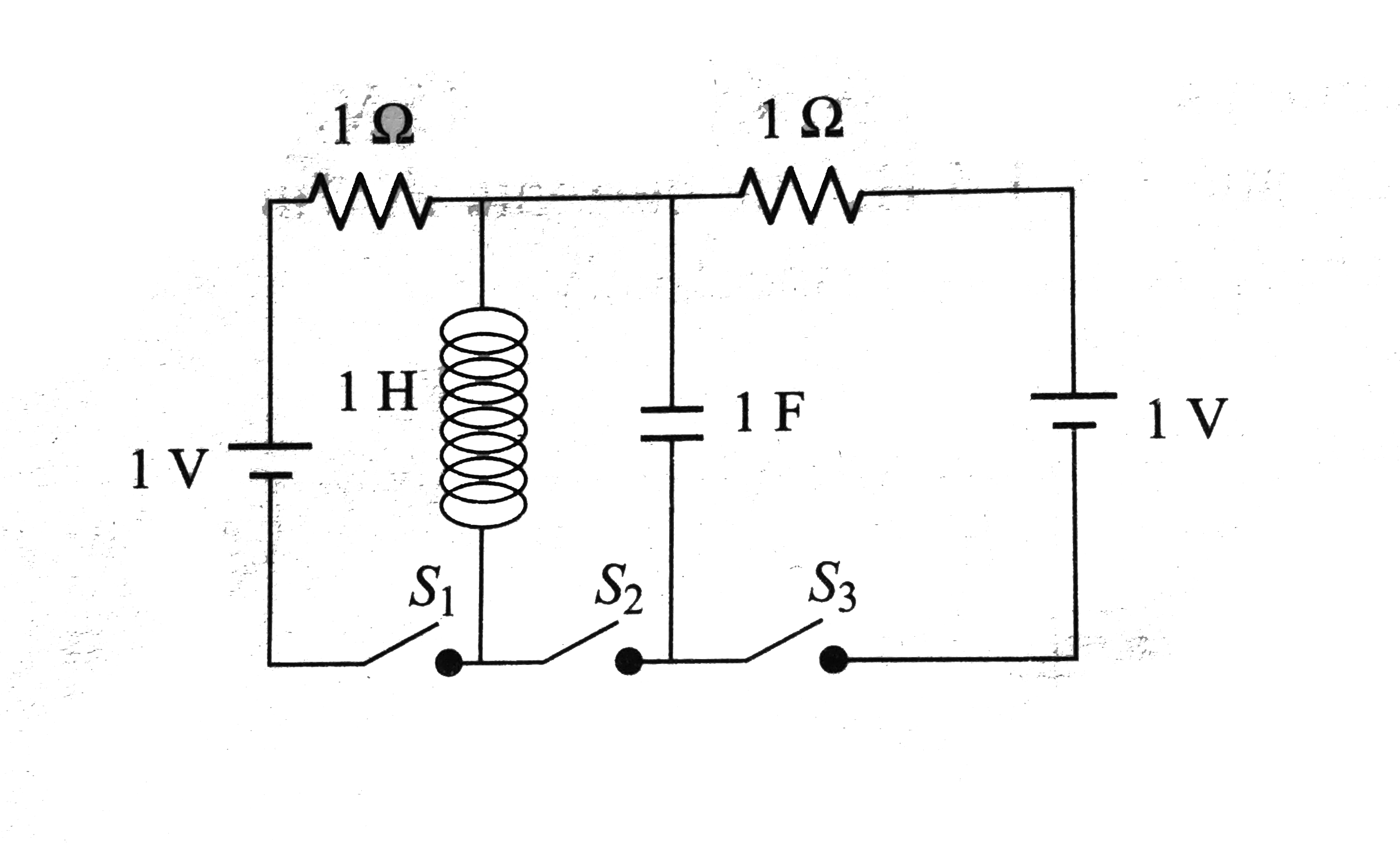
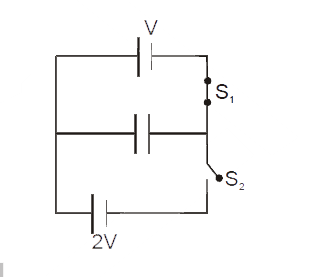
View SolutionAt any time S1 switch is opened and S2 is closed then find out heat generated in circuit.
View SolutionIn Fig. switch S is closed for a long time. At t=0, if it is opened, then

View SolutionIn Fig. switch S is closed for a long time. At t=0, if it is opened, then

View Solution