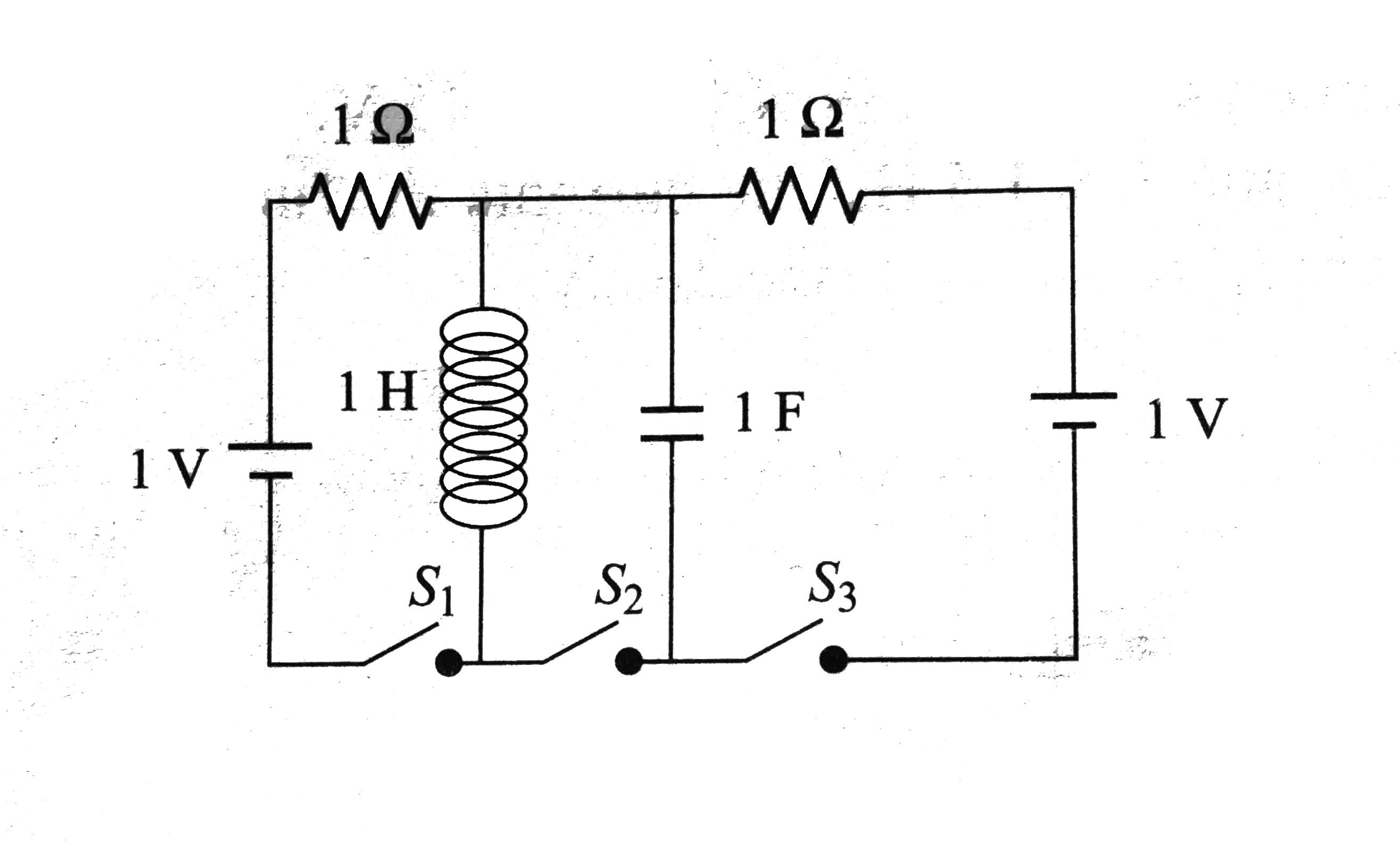
In the circuit shows (Fig.) switches S1 and S3 have been closed for 1s and S2 remained open. Just after 1s, switch S2 is closed and S1 and S3 are opened. Find after that instant (t=0):
the charge on the upper plate of the capacitor as a funtion of time
√2(1−1e)sin(t+3π4)
√2(1−1e)sin(t+π4)
√3(1−1e)sin(t+π4)
√3(1+1e)sin(t+π4)
The correct Answer is:A
S1 and S2 are closed for 1s.
Charge on capacitor,
q=CE(1−e−t/RC)=1−1e (i)
The current in inductor,
I=ER(1−e−t/RC)=1−1e(ii)
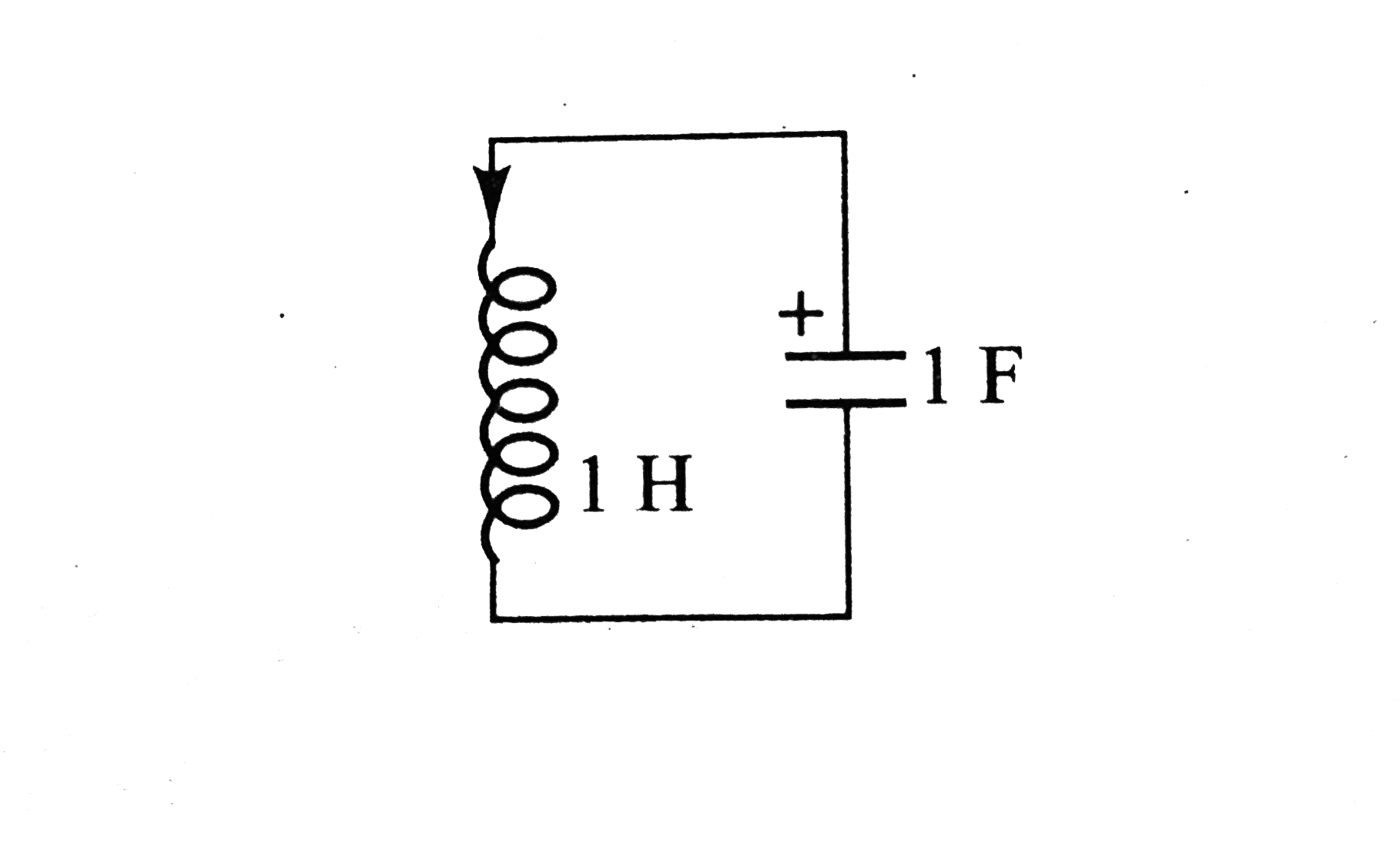
Now S1 and S3 are opened and S2 is closed,
It is LC circuit,
q=qmaxsin(ωt+ϕ) (iii)
I=(qmax)ωcos(ωt+ϕ) (iv)
As total energy (Magnetic + electrical) is constant
12LI2max=12q2maxC=12LI2+12q2C (v)
qmax=√2(1−1e) (vi)
Imax=√2(1−1e) (vii)
From (iii) at t=0, we get
(1−1e)=√2(1−1e)sinϕ⇒=π4 or 3π4
After closing S2, circuit will be as shows. Direction of current shows that charge on capacitor will be decreaseing. Hence ϕ=3π/4
q=√2(1−1e)sin(ωt+3π4)
where, ω=1√LC=1
q=√2(1−1e)sin(t+3π4)
Topper's Solved these Questions
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Exercises (integer)
8 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Archives (fills In The Blanks)
3 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Exercises (assertion-reasoning)
2 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICSCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
28 Videos
- KINETIC THEORYBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORYEXERCISE - Question Bank
31 Videos
Similar Questions
In the circuit shown switches S1 and S2 have been closed for 1sec and S2 remained open.Just after 1 second is over switch S2 is closed and S1,S3 are opened.Find after that instant The charge on the upper plate of the capacitor as function of time taking the instant of switching on of S2 and switching off all time switches to be t=0 is q=x×10−2cos(t+π4).Findout value of x.

View SolutionIn a circuit S1 remains closed for a long time and S2 remain open. Now S2 is closed and S1 is opened. Find out the di/dt in the right loop just after the moment.

View Solution
Knowledge Check
In the circuit shows (Fig.) switches S1 and S3 have been closed for 1s and S2 remained open. Just after 1s, switch S2 is closed and S1 and S3 are opened. Find after that instant (t=0):
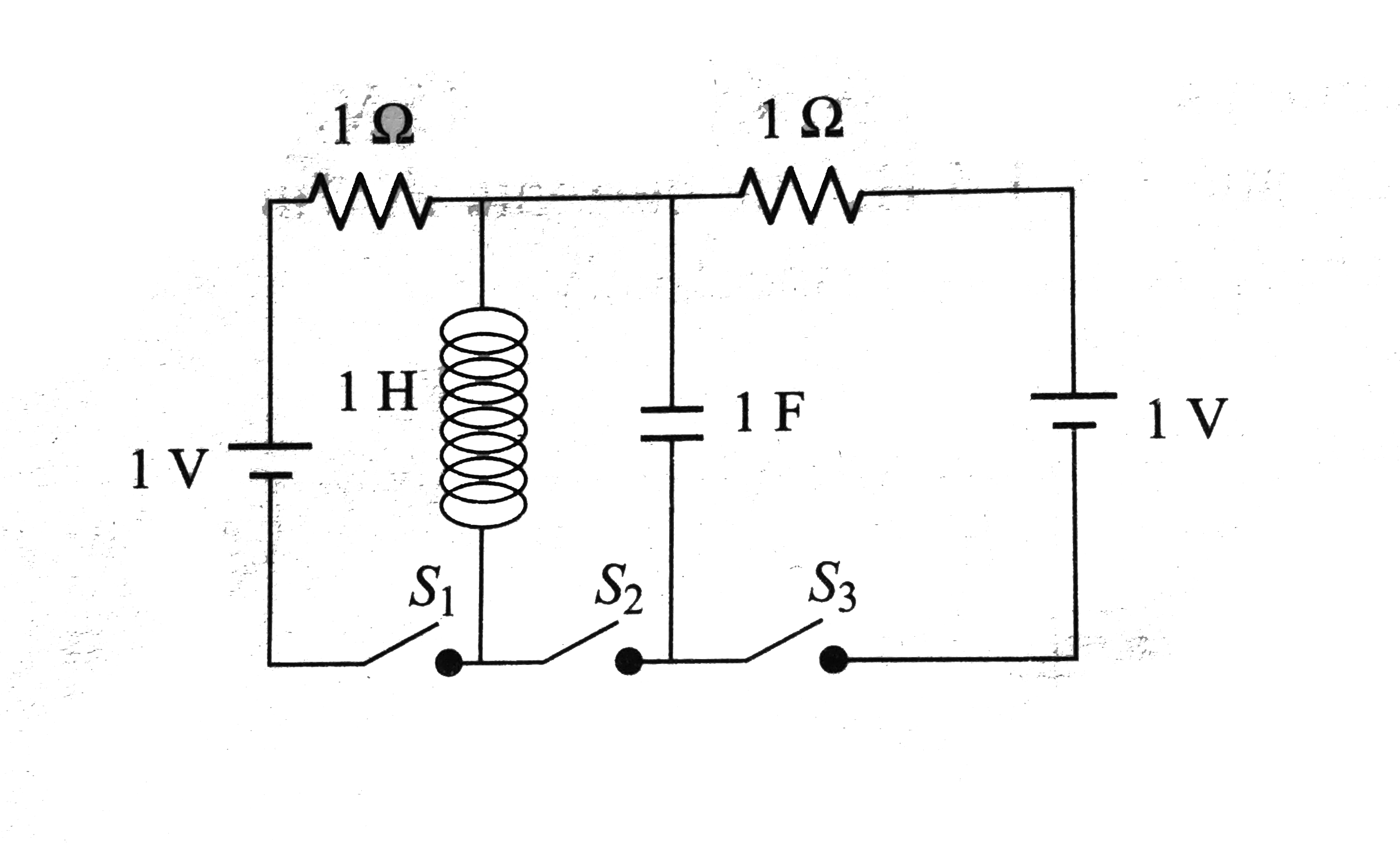
the maximum charge on the capacitorA√3(1+1e)B√3(1−1e)C√2(1+1e)D√2(1−1e)In the circuit shows (Fig.) switches S1 and S3 have been closed for 1s and S2 remained open. Just after 1s, switch S2 is closed and S1 and S3 are opened. Find after that instant (t=0):
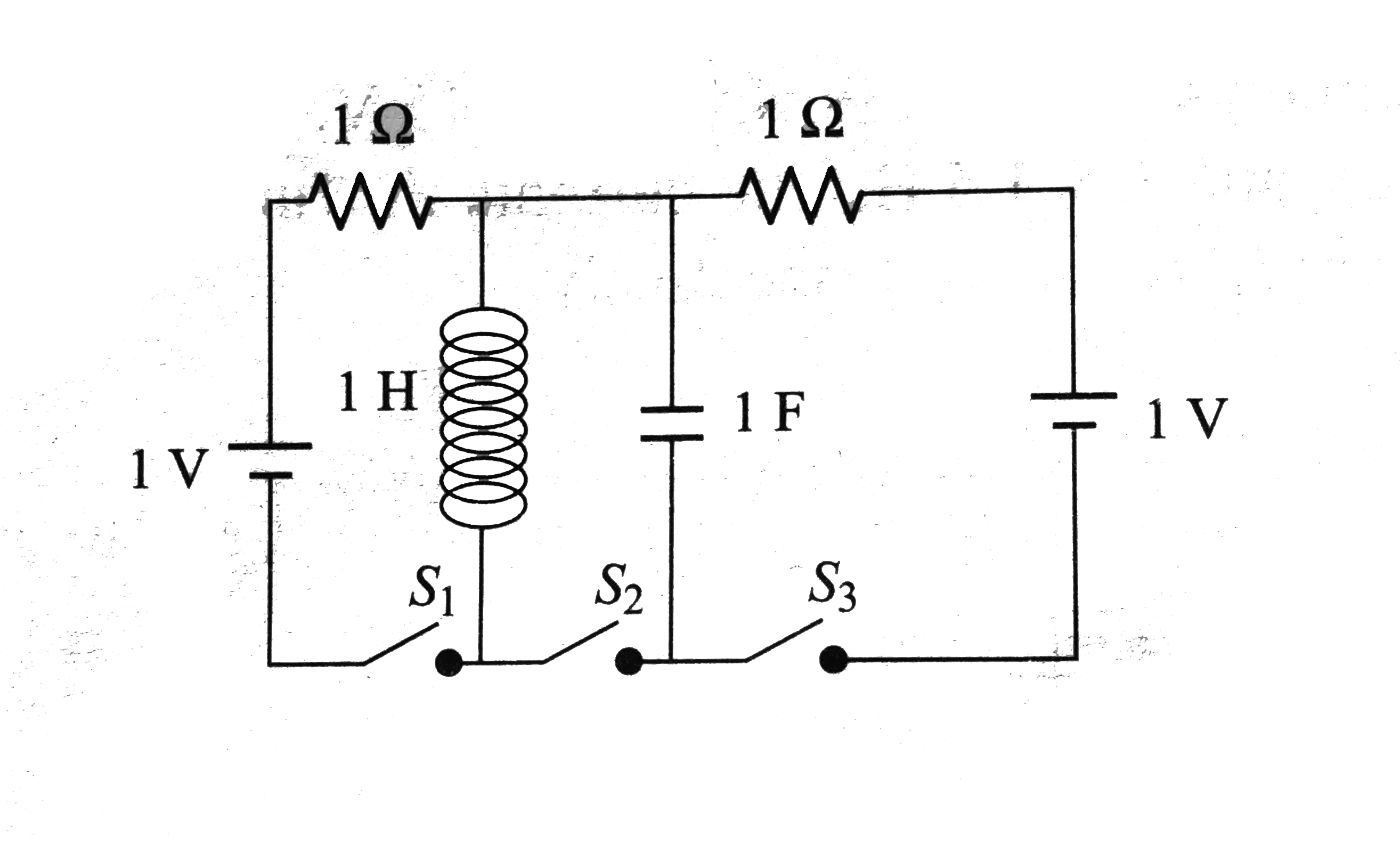
the maximum current in the circuit containing inductor and capacitor (only S2 is closed)A√3(1−1e)B√2(1−1e)C√3(1+1e)D√2(1+1e)In the circuit shown in the figure, if switches S1 and S2 have been closed for a long time, then charge on the capacitor.
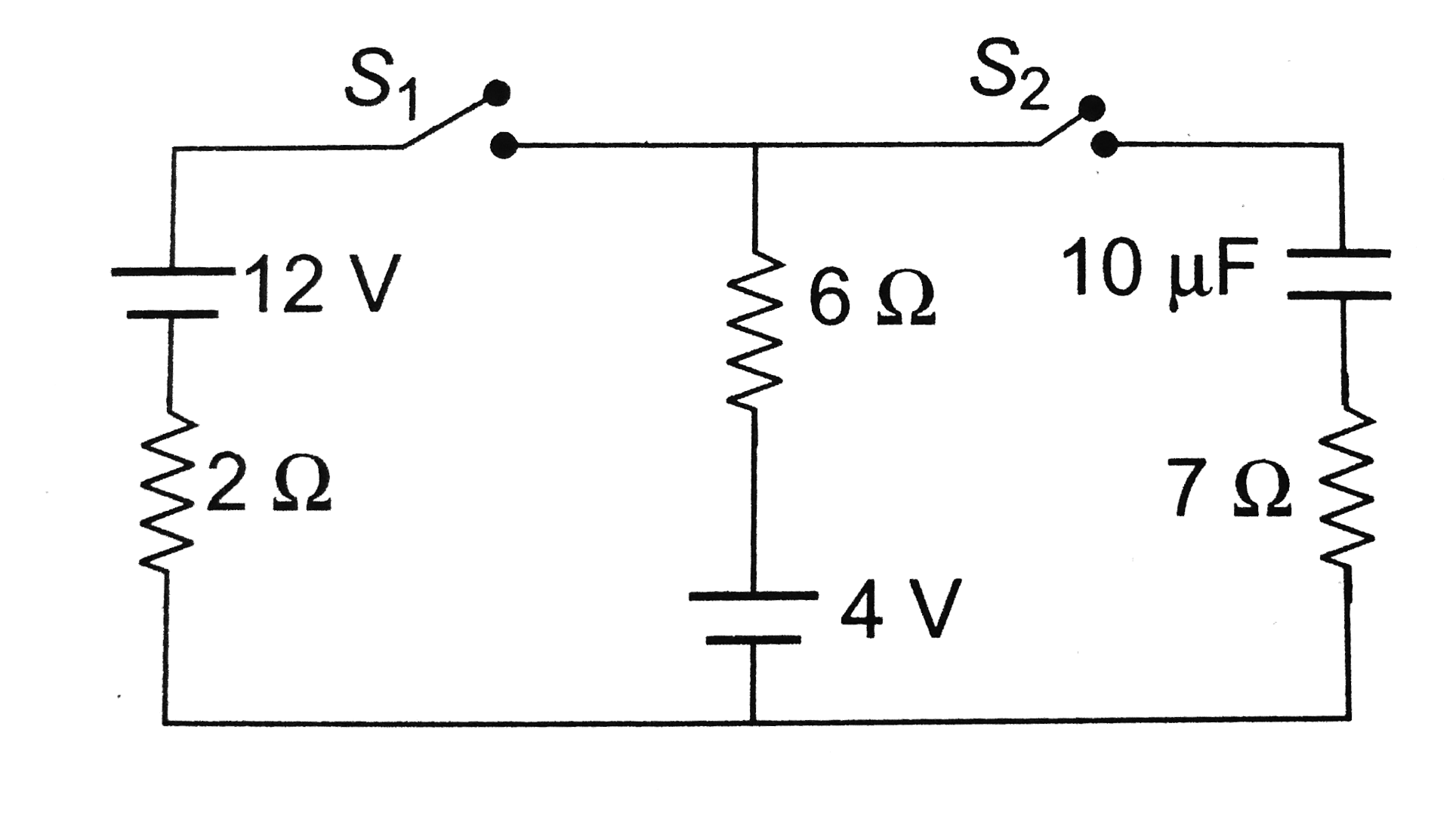 Ais 100μCBincreases to 200μC if one third of the gap of the capacitor's plates is filled with a dielectric (K=2) of same areaCboth (a) and (b) aboveDcharge on the capacitor remains unchanged if one third of the gap of the capacitor's plates is filled with a dielectric (K=2) of same area.
Ais 100μCBincreases to 200μC if one third of the gap of the capacitor's plates is filled with a dielectric (K=2) of same areaCboth (a) and (b) aboveDcharge on the capacitor remains unchanged if one third of the gap of the capacitor's plates is filled with a dielectric (K=2) of same area.
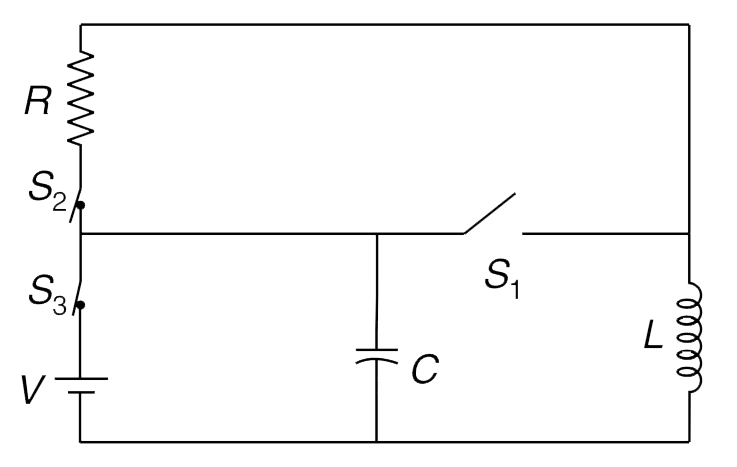
In the circuit shown in figure S1 is open and, S2 and S3 are closed. The circuit is in steady state. At time t = 0, switch S1 is closed and S2 and S3 are opened simultaneously. V=100volt,R=10Ω,C=100μF,L=0.03H
(a) Find the maximum charge that will appear on the capacitor at any time.
(b) Find the time at which the charge on the capacitor will become zero for the first time.
View SolutionAfter switch S2 is closed and S1 is opened, the maximum value of current through the inductor is:
View SolutionIn the arrangement as shown in the figure, S1 and S3 are already closed for a long time. Now at t=0 the S2 is closed and S1,S3 are opened [ ε=1 volt, L=1 henry, R=1Ω & C=1 Faraday ]

View SolutionIn the circuit shown, the switch S has been close for a long time. At time t=0 the switch is opened. It remains open for a long time T, after which it is closed again.

View SolutionIn the circuit shown, S2 is closed first and is kept closed for a long time. Now S1 is closed. Just after that instant the current through S1is

View Solution
