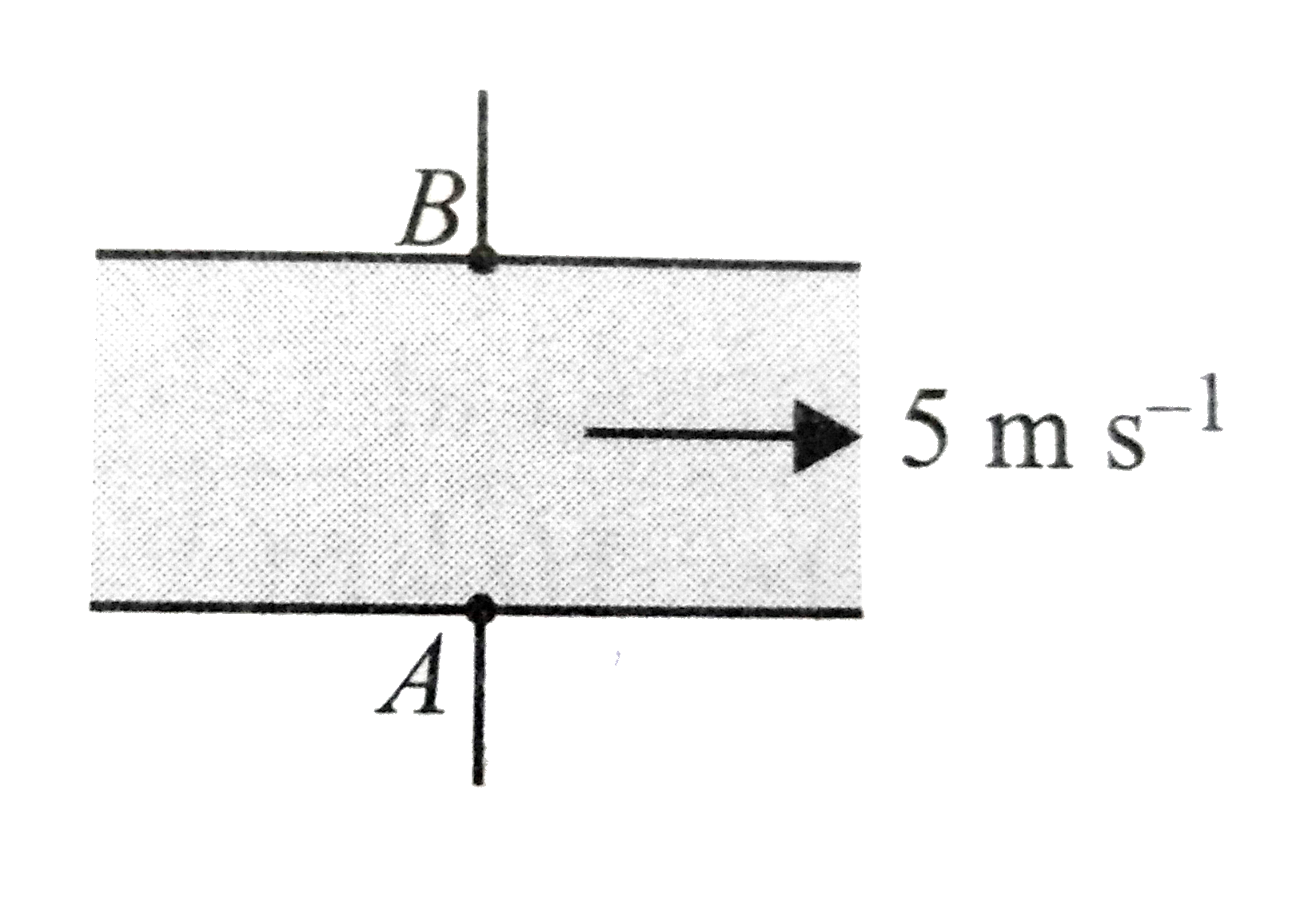
In the figure shown a river of width 4m is flowing with speed of 5m/s. A swimmer whose swimming speed relative to the water is 4ms, starts swimming from a point A on a bank. On the other bank B is a point which is directly opposite to A. What minimum distance (in m) the swimmer will have to walk on the other bank to reach the point B.
2
3
4
5
The correct Answer is:B
To solve the problem, we need to determine the minimum distance the swimmer will have to walk on the other bank to reach point B after swimming across the river.
1. Identify the Given Values:
- Width of the river (distance to swim across) = 4m
- Speed of the river = 5m/s
- Speed of the swimmer relative to the water = 4m/s
2. Determine the Time Taken to Swim Across the River:
- The time taken to swim across the river can be calculated using the formula:
Time=DistanceSpeed
- Here, the distance is the width of the river (4 m) and the speed of the swimmer relative to the water is 4 m/s.
- Therefore, the time taken to swim across is:
Time=4m4m/s=1s
3. Calculate the Drift Caused by the River:
- While the swimmer is swimming across, the river is also flowing. The swimmer will be carried downstream due to the river's current.
- The distance drifted downstream (BC) can be calculated using:
Distance=Speed×Time
- The speed of the river is 5 m/s and the time taken to swim across is 1 s.
- Thus, the distance drifted downstream is:
BC=5m/s×1s=5m
4. Conclusion:
- The swimmer will have to walk the distance BC on the other bank to reach point B. Therefore, the minimum distance he will have to walk is:
Distance BC=5m
Final Answer:
The minimum distance the swimmer will have to walk on the other bank to reach point B is 5 meters.
---
- Width of the river (distance to swim across) = 4m
- Speed of the river = 5m/s
- Speed of the swimmer relative to the water = 4m/s
- The time taken to swim across the river can be calculated using the formula:
Time=DistanceSpeed
- Here, the distance is the width of the river (4 m) and the speed of the swimmer relative to the water is 4 m/s.
- Therefore, the time taken to swim across is:
Time=4m4m/s=1s
- While the swimmer is swimming across, the river is also flowing. The swimmer will be carried downstream due to the river's current.
- The distance drifted downstream (BC) can be calculated using:
Distance=Speed×Time
- The speed of the river is 5 m/s and the time taken to swim across is 1 s.
- Thus, the distance drifted downstream is:
BC=5m/s×1s=5m
- The swimmer will have to walk the distance BC on the other bank to reach point B. Therefore, the minimum distance he will have to walk is:
Distance BC=5m
The minimum distance the swimmer will have to walk on the other bank to reach point B is 5 meters.
Topper's Solved these Questions
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - MCQ_TYPE
27 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - COMPREHENSION_TYPE
19 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
Similar Questions
The speed of a man in a ponds is double that of the water ina river. The man starts swimming from a polints P on the bank. What is the angle of swimming of the man so as to directly to the opposite bank?
View SolutionA river is flowing from west to east with a speed 5m/s. A swimmer can swim in still water at a speed of 10m/s .
If he wants to start from point A on south bank and reach opposite point B on north bank. In what direction direction should he swim ?
View SolutionA swimmer wants to cross a 200 m wide river which is flowing at a speed of 2 m/s. the velocity of the swimmer with respect to the river is 1 m/s. how far from the point directly opposite to the starting point does the swimmer reach the opposite bank ?
View SolutionA river is flowing due east with a speed 3ms−1 A swimmer can swim in still water at a speed of 4ms−1 If swimmer starts swimming due north what will be his resultant velocity (magnitude and direction )?
View SolutionA man wishes to cross a river of width 120 m by a motorboat. His rowing speed in still water is 3m/s and his maximum walking speed is 1m/s. The river flows with velocity of 4m/s.
(a) Find the path which he should take to get to the point directly opposite to his starting point in the shortest time.
(b) Also, find the time which he takes to reach his destination.
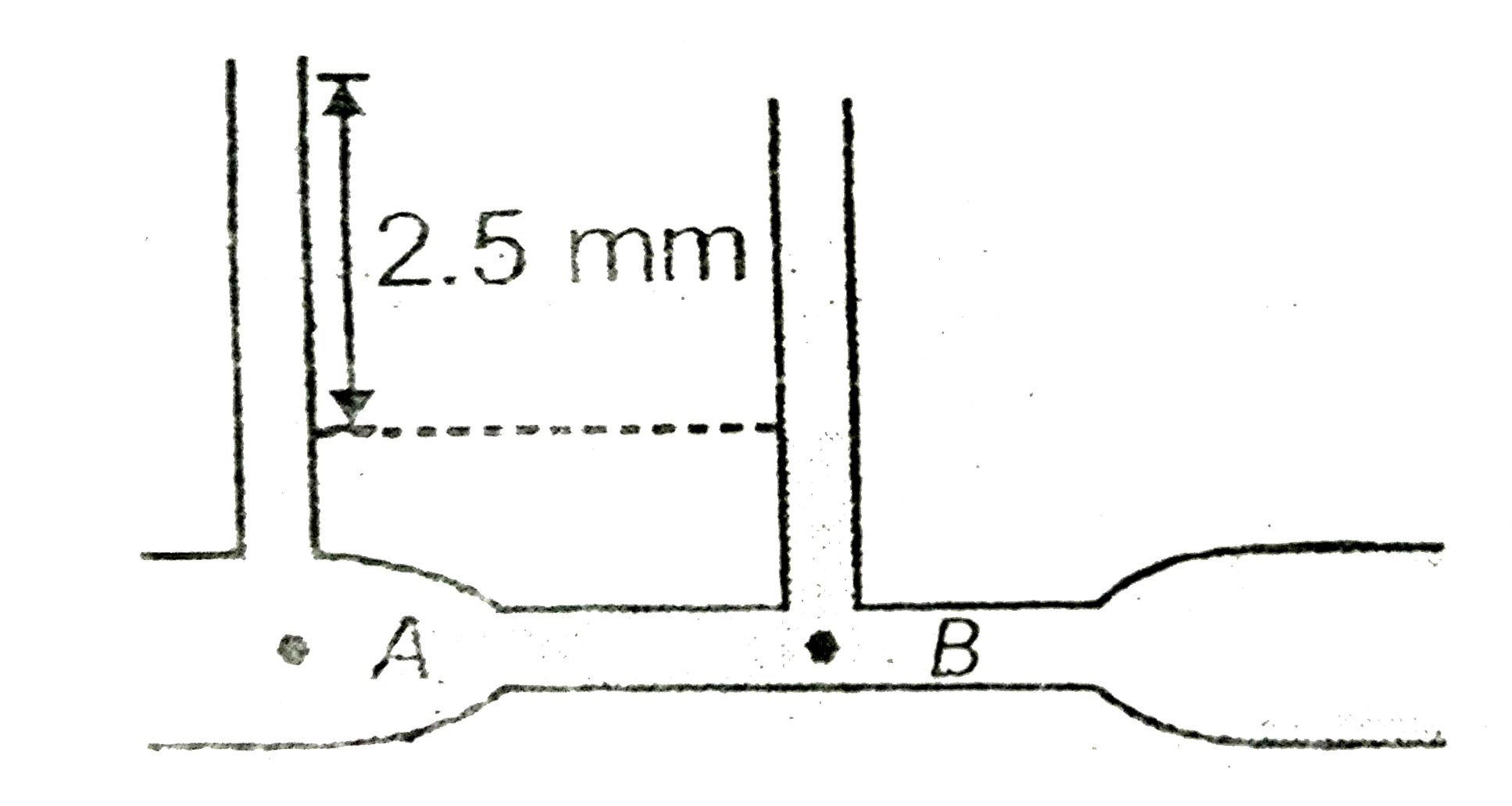
View SolutionIn the figure shown below, a fluid of density 2×103 kg m−3 is flowing in a horizontal pipe. The speed of water at point A is 4 cm s−1, what is its speed at point B?
View SolutionA river of width 80m is flowing at 6 m/s. A motorboat crosses the river in 10s and reaches a point directly across on the other river bank. The velocity of motorboat in still water is :
View SolutionA river is of width 120m which flows at a speed pf 8ms−1. If a man swims with a speed of 5ms−1 at an angle of 127∘ with the stream, his drift on reaching other bank is
View SolutionVelocity of the boat with respect to river is 10m/s. From point A it is steered in the direction shown. Where will it reach on the opposite bank ?

View SolutionA river flows with a speed more than the maximum speed with which a person can swim in still water. He intends to cross the river by the shortest possible path (i.e., he wants to reach the point on the opposite bank which directly opposite to the starting point). Which of the following is correct ?
View Solution
