In the figure shown, a spring of spring constant K is fixed at on end and the other end is attached to the mass 'm' . The coefficient of friction between block and the inclined plane is μ. The block is released when the spring is in tis natural length. Assuming that the θ>μ, the maximum speed of the block during the motion is.
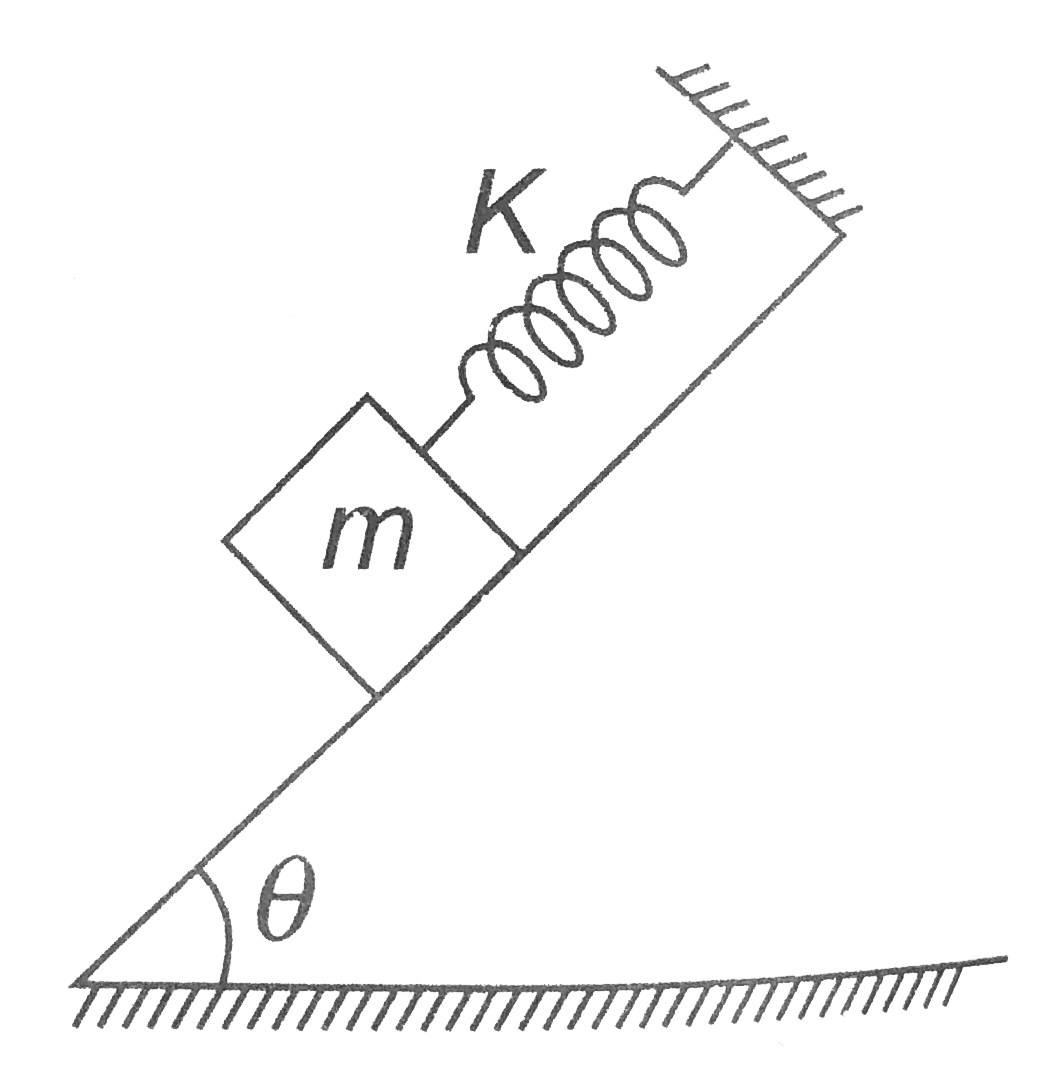
(cosθ+μsinθ)g√mk
(cosθ−μsinθ)g√mk
(sinθ+μcosθ)g√mk
(sinθ−μcosθ)g√mk
The speed is maximum when acceleration is least
Let displacment of block is x0 when the speed of block maximum.
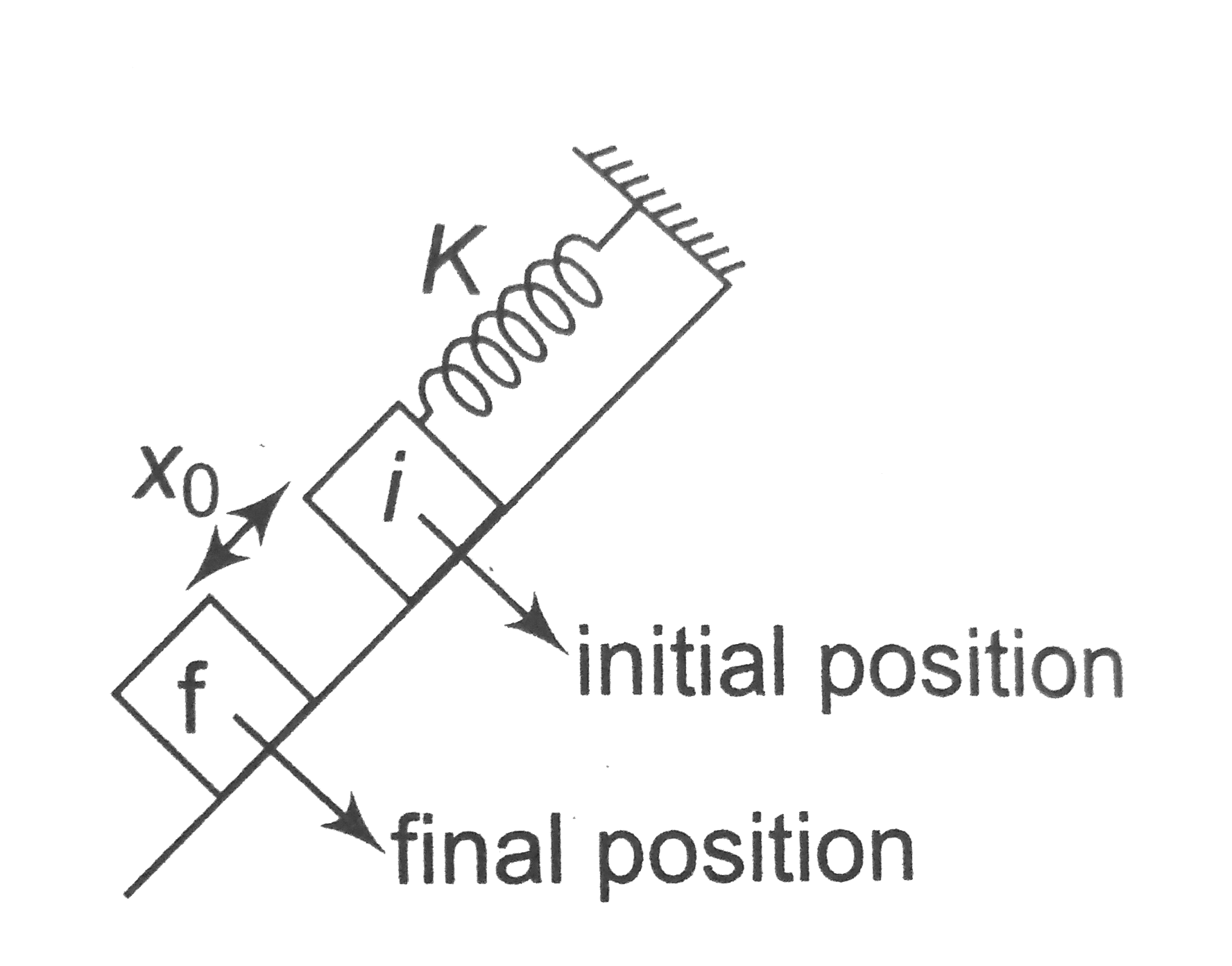
At displacement , applying Newton's law to the block along the incline
mgsinθ=μmgcosθ+kx0 (1)
Applying work energy theorem to block along and final position is
kf=ki+mgx0sinθ−12kx20−μmgx0cosθ (2)
Solving (1) and (2) we get,
Vmax=(sinθ−μcosθ)g√mk
Topper's Solved these Questions
Similar Questions
The block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

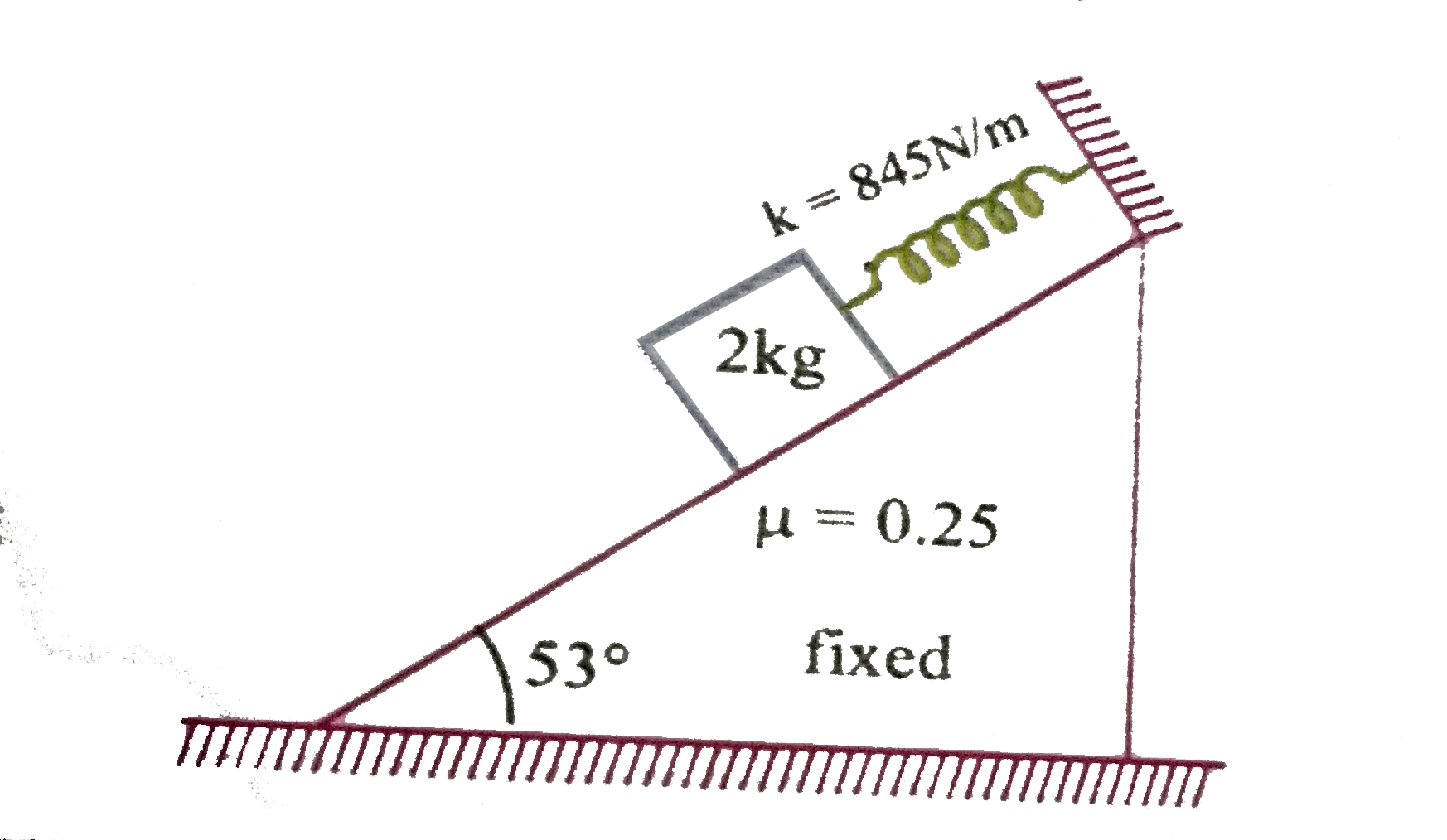
View SolutionA block of mass 2kg is placed on an inclined plane of angle 53∘, attached with a spring as shown. Friction coefficient between block and the incline is 0.25. The block is released from the rest and when spring is in natural length. Find maximum speed of the block it acquires after the release in cm//s is found to be nearly 5n. Find 'n'(takeg=10m/s2).
 .
.
View Solution
Knowledge Check
A block is stationary on an inclined plane If the coefficient of friction between the block and the plane is μ then
 .Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ
.Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
AmgBmgsinθ√1+μ2CmgsinθD√(mgsinθ)2+(μmgcosθ)2A block of mass m slides down an inclined plane of inclination θ with uniform speed The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is .
Amgsinθ√1+μ2B√(mgsinθ)2+(μmgcosθ)2CmgsinθDmg
A block of mass m is placed at rest on an inclination θ to the horizontal.If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View SolutionThe left end of the spring tied to a wall and at the right end is attached to a block of mass m, which is placed on a frictionless ground. The force F displaces the block by distance x where it is exactly balanced by the spring force.
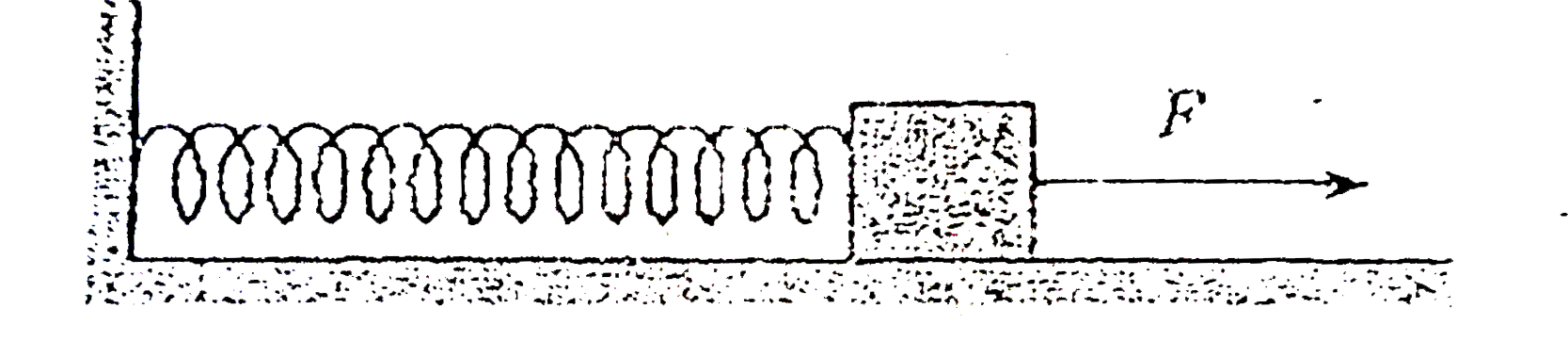
What is the maximum speed of the block in the ensuing motion after the force F is removed?
View SolutionIn the system as shown in figure, the blocks have masses m1 and m2, the spring constant is k, coefficient of friction between the block of mass m1 and the surface is μ. The system is released with zero initial speed from the position where the spring is in its natural length.

View SolutionA block of mass m is placed on a rough plane inclined at an angle θ with the horizontal. The coefficient of friction between the block and inclined plane is μ . Ifθ<tan−1(μ) , then net contact force exerted by the plane on the block is :
View SolutionA system of wedge and block as shown in figure, is released with the spring in its natural length. All surfaces are frictionless. Maximum elongation in the spring will be
 .
.
View Solution
