In the figure shown, find.
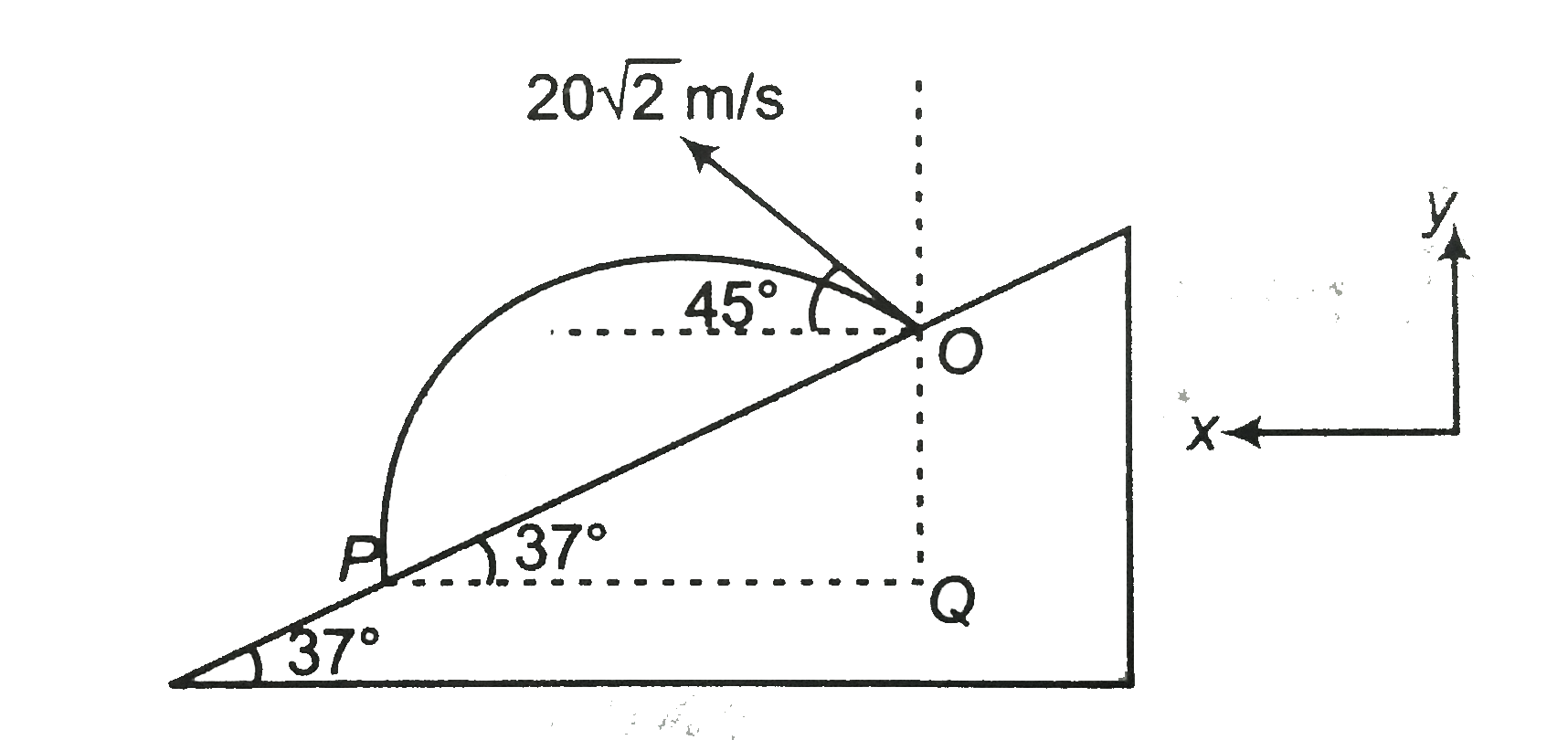
(a) time of flight of the projectile along the inclined plane.
(b) range OP.
The correct Answer is:A, B
(a) Horizontal component of initial velocity, ux=20√2cos45∘=20m/s
Vertical component of initial velocity,
uy=20√2sin45∘=20m/s
Let the particle, strikes the inclined plane at P after time t, then horizontal displacement
QP=uxt=20t
In vertical displacement, uytor20t is upward and 12gt2or5t2 is downwards. But net vertical
displacement is downwards. Hence 5t2 should be greater than 20 t and therefore,
OQ=5t2−20t
In ΔOQP,
tan37∘=OQQP
or 34=5t2−20t20t
Solving this equation, we get
t=7s
(b) Range, OP =(PQ)sec37∘
=(20t)(54)
Substituting the value of t, we get
OP=175m.
Topper's Solved these Questions
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Miscellaneous Examples
4 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Exercise 7.1
5 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Example Type 4
1 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery
32 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
Similar Questions
Knowledge Check
The time of flight of projectile on an upward inclined plane depends upon.
Aangle of projectionBangle of inclination of the planeCair resistanceDa and b both
In the figure shown

find the range R.
View SolutionFind time of flight and range of the projectile along the inclined plane as shown in figure. (g=10m/s2)
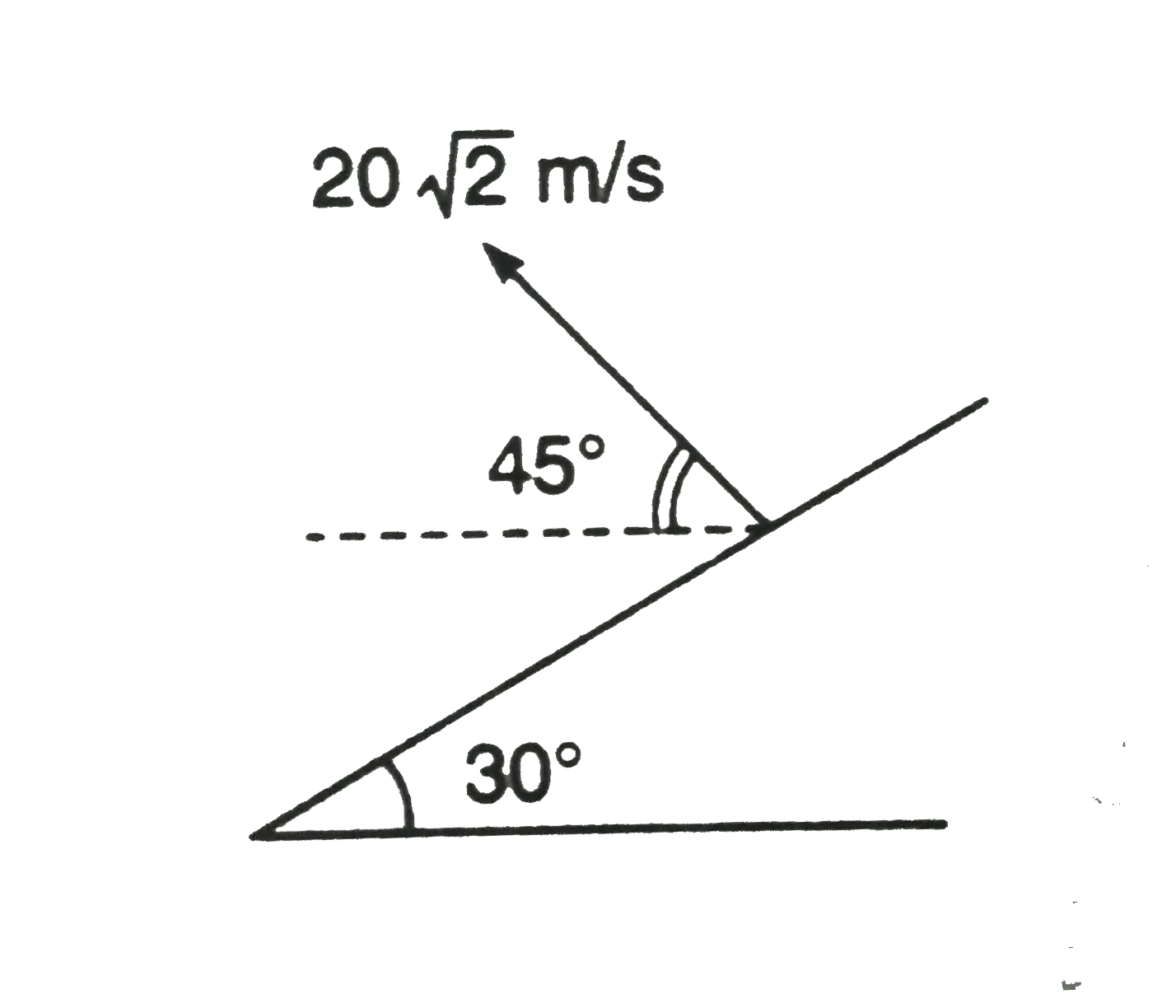
View SolutionFind time of flight and range of the projectile along the inclined plane as shown in figure. (g=10m/s2)
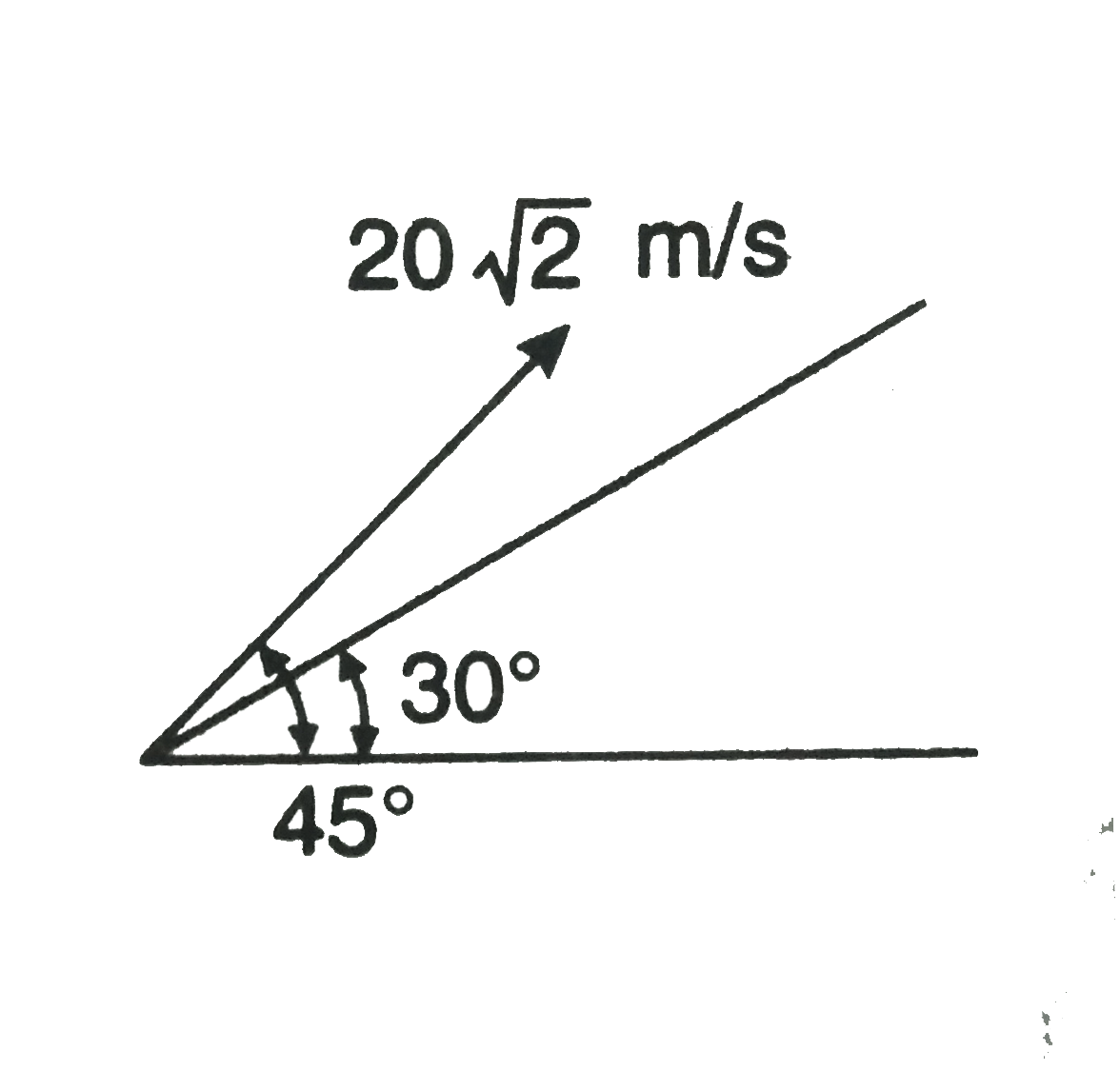
View SolutionFind time of flight and range of the projectile along the inclined plane as shown in figure. (g=10m/s2)
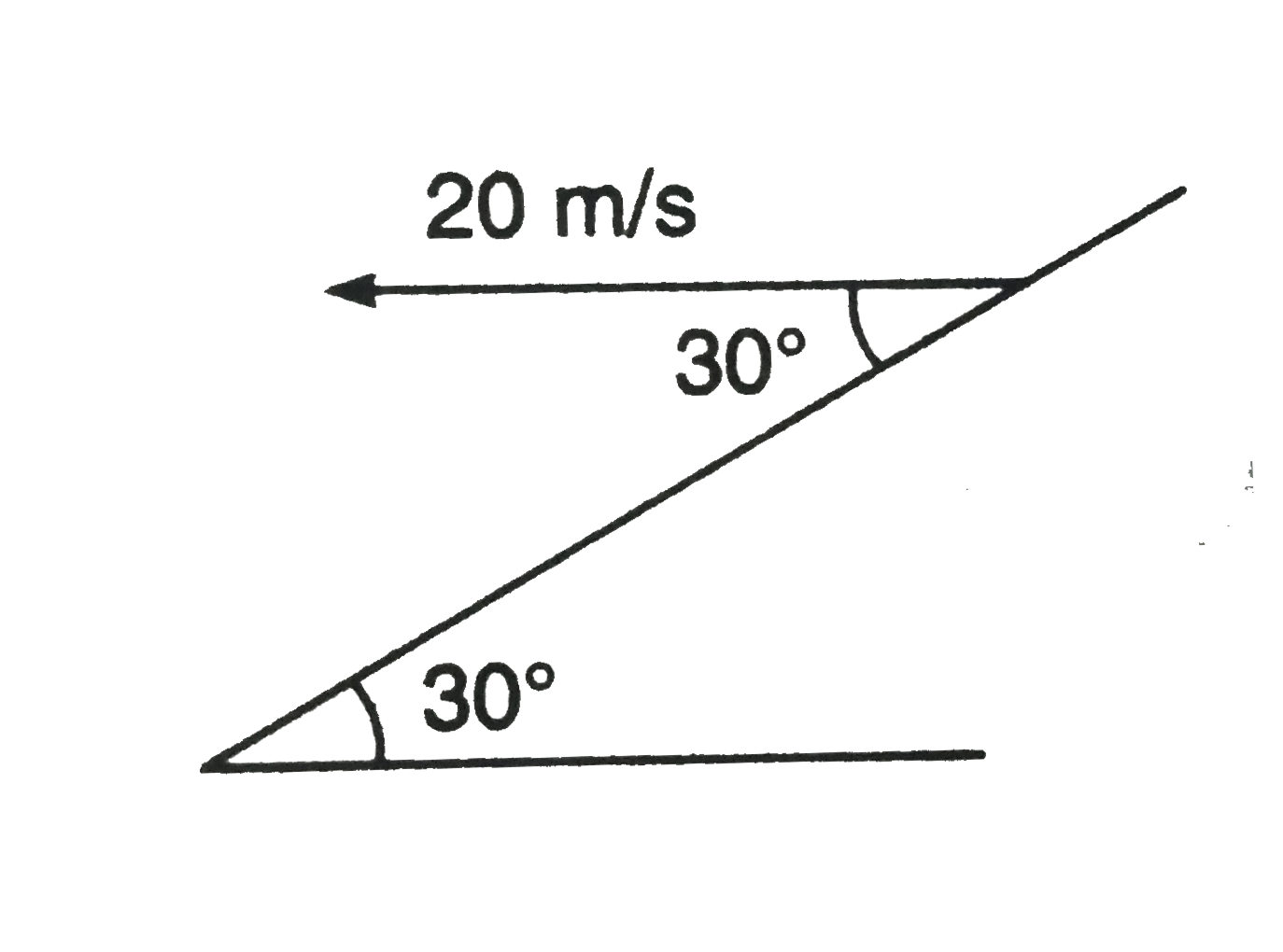
View SolutionA projectile is fired with a velocity v at right angle to the slope inclined at an angle θ with the horizontal. The range of the projectile along the inclined plane is
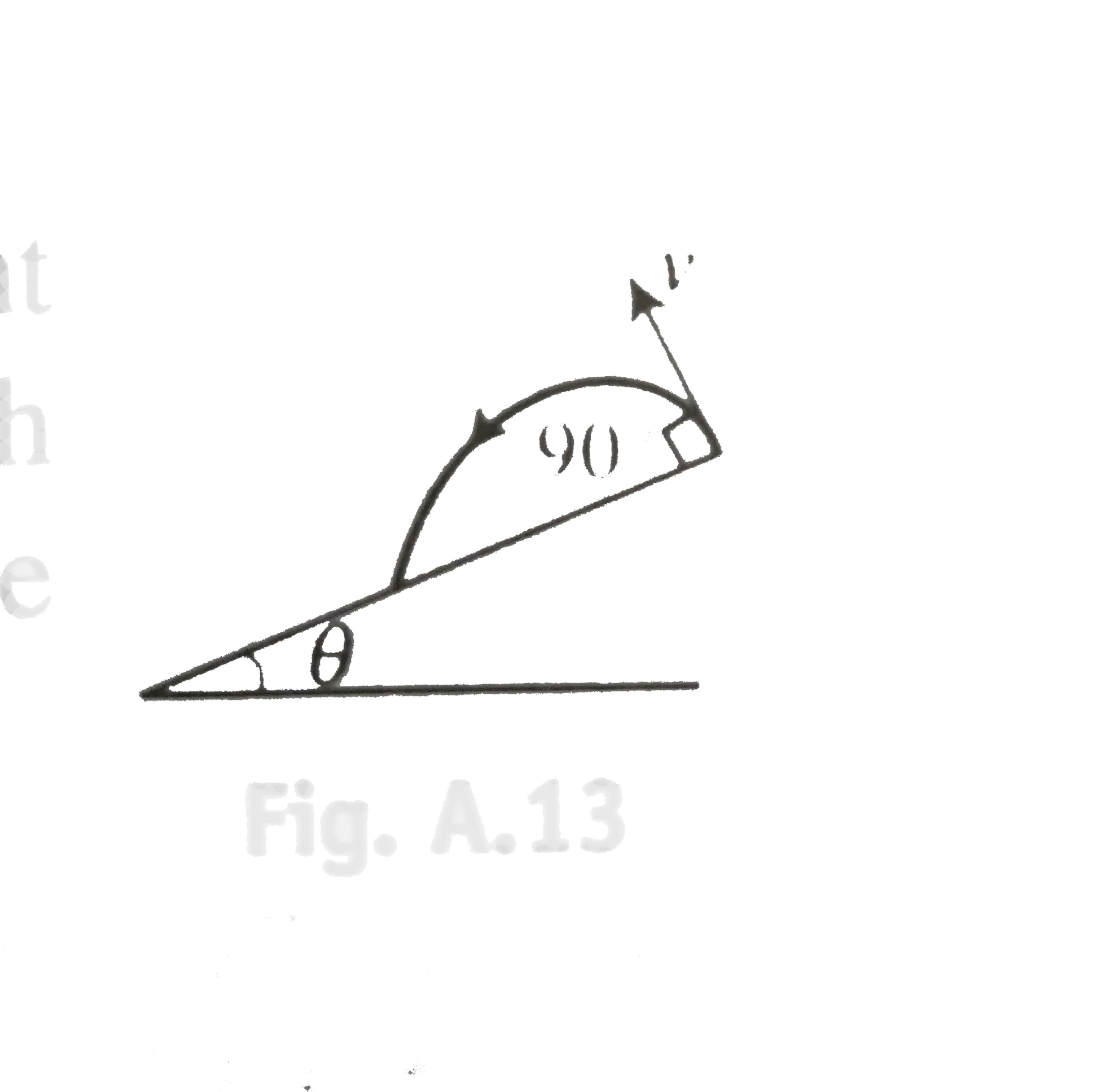
View SolutionA particle is projected on an inclined plane with a speed u as shown in (Fig. 5.61). Find the range of the particle on the inclined plane.
 .
.
View SolutionA bullet is fired from the bottom of the inclined plane at angle θ=37∘ with the inclined plane. The angle of incline is 30∘ with the horizontal. Find the
(a) position of the maximum height of the bullet from the inclined plane ,
(b) time of light ,
( c) range along the incline ,
(d) the value of θ at which the range will be maximum ,
( e) maximum range.
View Solution

 .
.