A bullet is fired from the bottom of the inclined plane at angle θ=37∘ with the inclined plane. The angle of incline is 30∘ with the horizontal. Find the
(a) position of the maximum height of the bullet from the inclined plane ,
(b) time of light ,
( c) range along the incline ,
(d) the value of θ at which the range will be maximum ,
( e) maximum range.
To solve the problem step-by-step, we will break down each part of the question regarding the bullet fired from the inclined plane.
Given Data:
- Angle of inclination of the plane, α=30∘
- Angle of projection of the bullet with respect to the inclined plane, θ=37∘
- Acceleration due to gravity, g
Step 1: Analyze the Motion
We will resolve the initial velocity u of the bullet into two components:
- Along the inclined plane (x-direction): ux=ucos(θ)
- Perpendicular to the inclined plane (y-direction): uy=usin(θ)
Step 2: Time of Flight (T)
Using the vertical motion equation, we can find the time of flight. The vertical motion is affected by gravity, which acts perpendicular to the inclined plane. The effective acceleration in the y-direction is:
gy=gcos(α)
The equation for vertical motion is:
s=uyt+12(−gy)t2
At maximum height, the displacement s=0 (it goes up and comes back down):
0=usin(θ)t−12gcos(α)t2
Rearranging gives:
usin(θ)t=12gcos(α)t2
Dividing by t (assuming t≠0):
usin(θ)=12gcos(α)t
Thus, the time of flight T is:
T=2usin(θ)gcos(α)
Step 3: Maximum Height (H)
The maximum height from the inclined plane can be calculated using:
H=u2y2gy
Substituting uy=usin(θ) and gy=gcos(α):
H=(usin(θ))22gcos(α)
Step 4: Range Along the Incline (R)
The range along the incline can be calculated using:
R=ux⋅T
Substituting ux=ucos(θ) and T:
R=ucos(θ)⋅2usin(θ)gcos(α)
This simplifies to:
R=2u2sin(θ)cos(θ)gcos(α)
Step 5: Angle for Maximum Range
To find the angle θ for maximum range, we differentiate the range equation with respect to θ and set it to zero. The maximum range occurs when:
θ+α=45∘
Thus,
θ=45∘−α=45∘−30∘=15∘
Step 6: Maximum Range
Substituting θ=15∘ into the range formula gives:
Rmax=u2sin(2(15∘+30∘))g=u2sin(90∘)g=u2g
Summary of Results:
(a) Maximum height from the inclined plane:
H=(usin(37∘))22gcos(30∘)
(b) Time of flight:
T=2usin(37∘)gcos(30∘)
(c) Range along the incline:
R=2u2sin(37∘)cos(37∘)gcos(30∘)
(d) Angle θ for maximum range:
θ=15∘
(e) Maximum range:
Rmax=u2g
- Angle of inclination of the plane, α=30∘
- Angle of projection of the bullet with respect to the inclined plane, θ=37∘
- Acceleration due to gravity, g
We will resolve the initial velocity u of the bullet into two components:
- Along the inclined plane (x-direction): ux=ucos(θ)
- Perpendicular to the inclined plane (y-direction): uy=usin(θ)
Using the vertical motion equation, we can find the time of flight. The vertical motion is affected by gravity, which acts perpendicular to the inclined plane. The effective acceleration in the y-direction is:
gy=gcos(α)
s=uyt+12(−gy)t2
At maximum height, the displacement s=0 (it goes up and comes back down):
0=usin(θ)t−12gcos(α)t2
Rearranging gives:
usin(θ)t=12gcos(α)t2
Dividing by t (assuming t≠0):
usin(θ)=12gcos(α)t
Thus, the time of flight T is:
T=2usin(θ)gcos(α)
The maximum height from the inclined plane can be calculated using:
H=u2y2gy
Substituting uy=usin(θ) and gy=gcos(α):
H=(usin(θ))22gcos(α)
The range along the incline can be calculated using:
R=ux⋅T
Substituting ux=ucos(θ) and T:
R=ucos(θ)⋅2usin(θ)gcos(α)
This simplifies to:
R=2u2sin(θ)cos(θ)gcos(α)
To find the angle θ for maximum range, we differentiate the range equation with respect to θ and set it to zero. The maximum range occurs when:
θ+α=45∘
Thus,
θ=45∘−α=45∘−30∘=15∘
Substituting θ=15∘ into the range formula gives:
Rmax=u2sin(2(15∘+30∘))g=u2sin(90∘)g=u2g
(a) Maximum height from the inclined plane:
H=(usin(37∘))22gcos(30∘)
T=2usin(37∘)gcos(30∘)
R=2u2sin(37∘)cos(37∘)gcos(30∘)
θ=15∘
Rmax=u2g
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.3
12 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.4
11 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.1
15 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
A particle is projected from the inclined plane at angle 37∘ with the inclined plane in upward direction with speed 10m/s. The angle of inclined plane with horizontal is 53∘. Then the maximum height attained by the particle from the inclined plane will be-
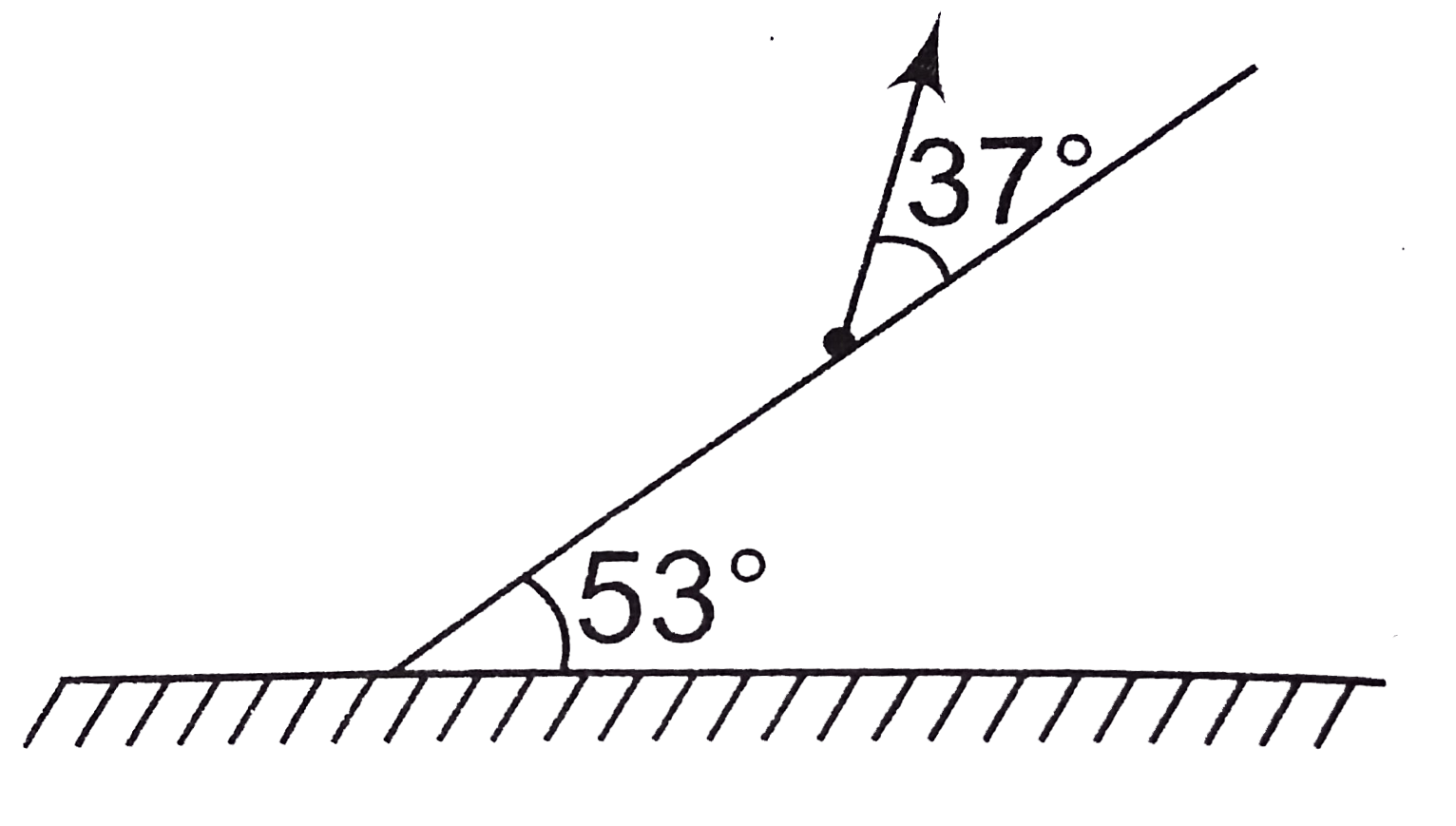
View SolutionA ball is projected from the bottom of an inclined plane of inclination 30∘, with a velocity of 30ms−1, at an angle of 30∘ with the inclined plane. If g=10ms−2 , then the range of the ball on given inclined plane is
View SolutionIn the figure shown, find.
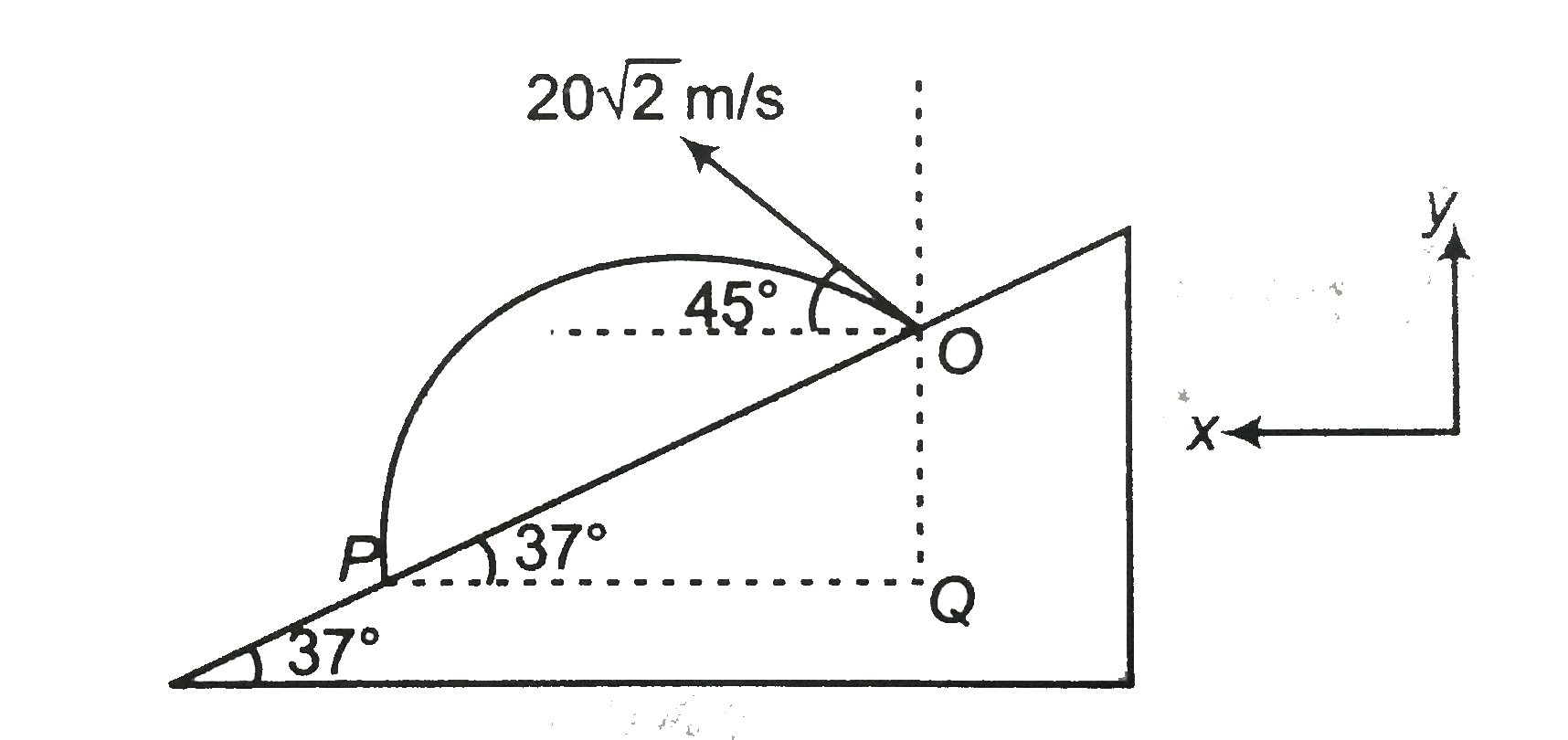
(a) time of flight of the projectile along the inclined plane.
(b) range OP.
View SolutionIn the figure shown, find.
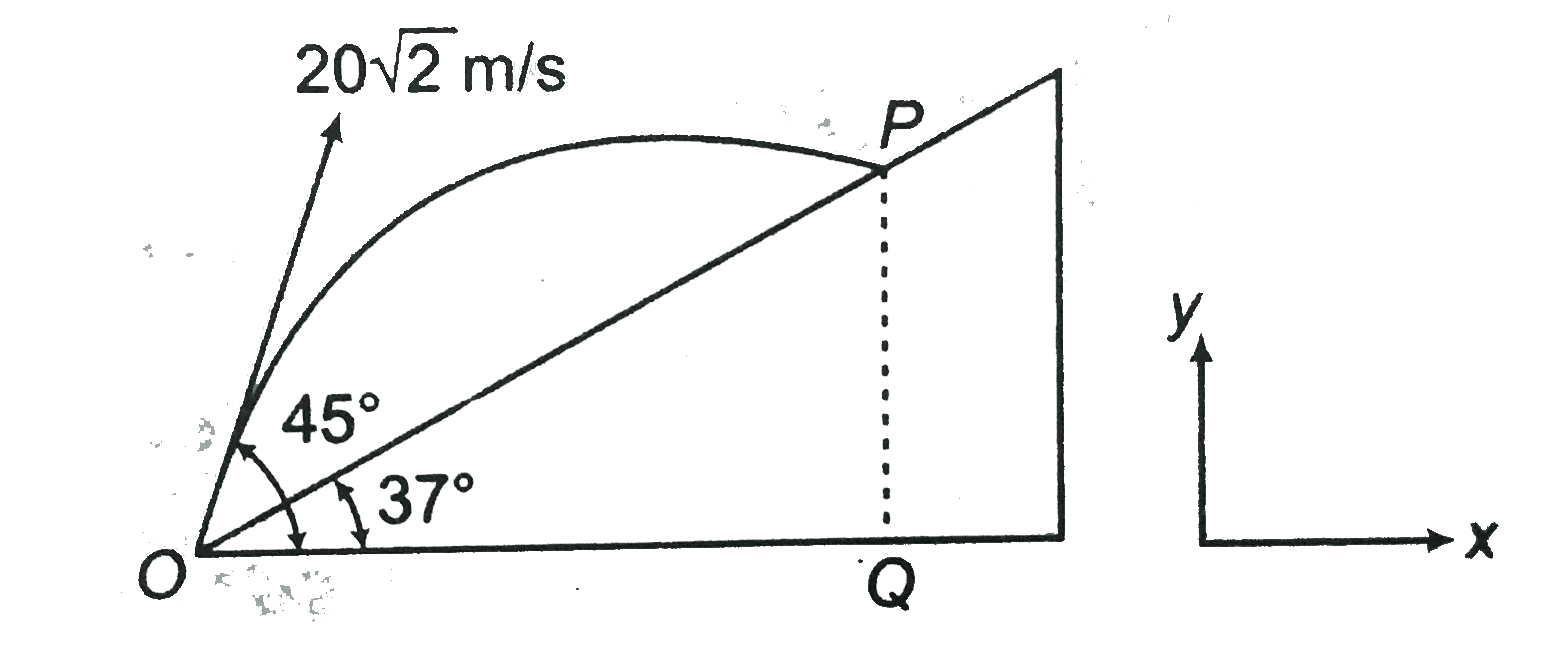
(a) time of flight of the projectile along the inclined plane.
(b) range OP.
View SolutionA trolley containing a liquid slides down a smooth inclined plane of angle α with the horizontal. Find the angle of inclination θ of the free surface with the horizontal.

View SolutionA box is placed on an inclined plane and has to be pushed down.The angle of inclination is
View SolutionA particle is projected from the bottom of an inclined plane of inclination 30∘. At what angle α (from the horizontal) should the particle be projected to get the maximum range on the inclined plane.
View SolutionThe maximum range of a rifle bullet on the horizontal ground is 6km. Find its maximum range on an inclined of 30∘.
View SolutionA projectile is fired with a velocity v at right angle to the slope inclined at an angle θ with the horizontal. The range of the projectile along the inclined plane is

View SolutionAn inclined plane makes an angle θ0=30∘ with the horizontal. A particle is projected from this plane with a speed of 5ms−1 at an angle of elevation β=30∘ with the horizontal as shown in (Fig. 5.53).
(a) Find the range of the particle on the plane when it strikes the plane.
(b) Find the range of the particle for β=120∘.
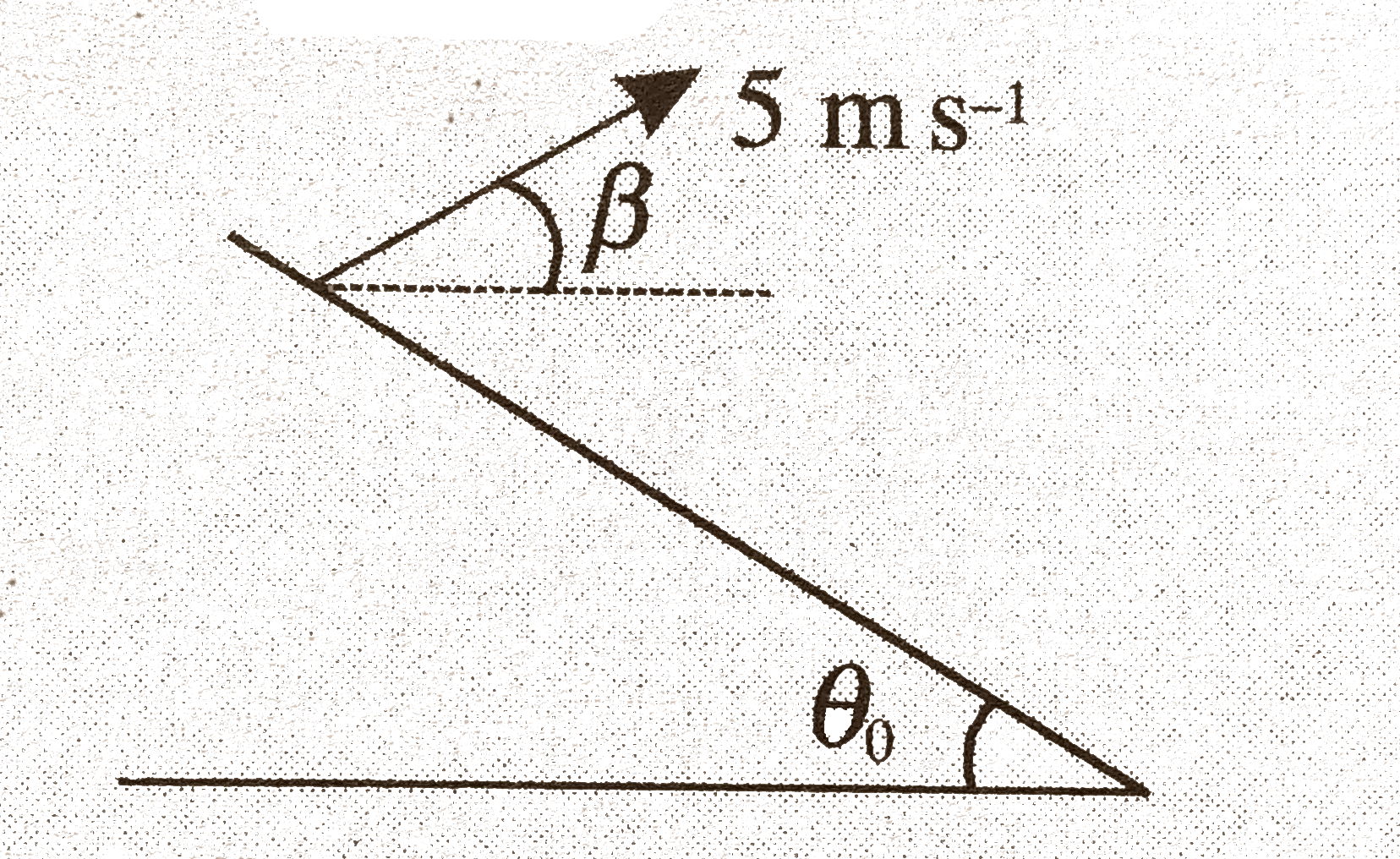 .
.
View Solution
