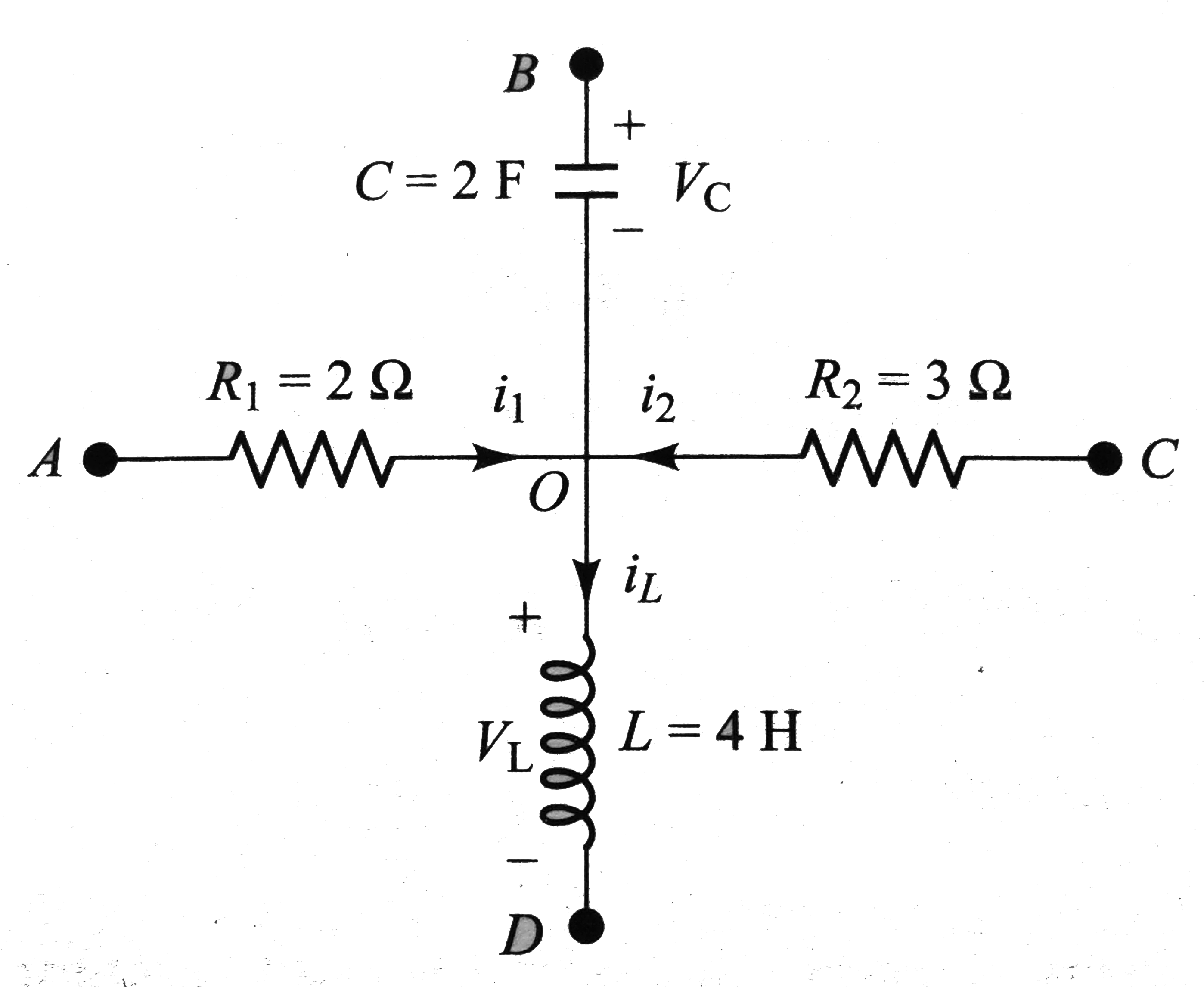
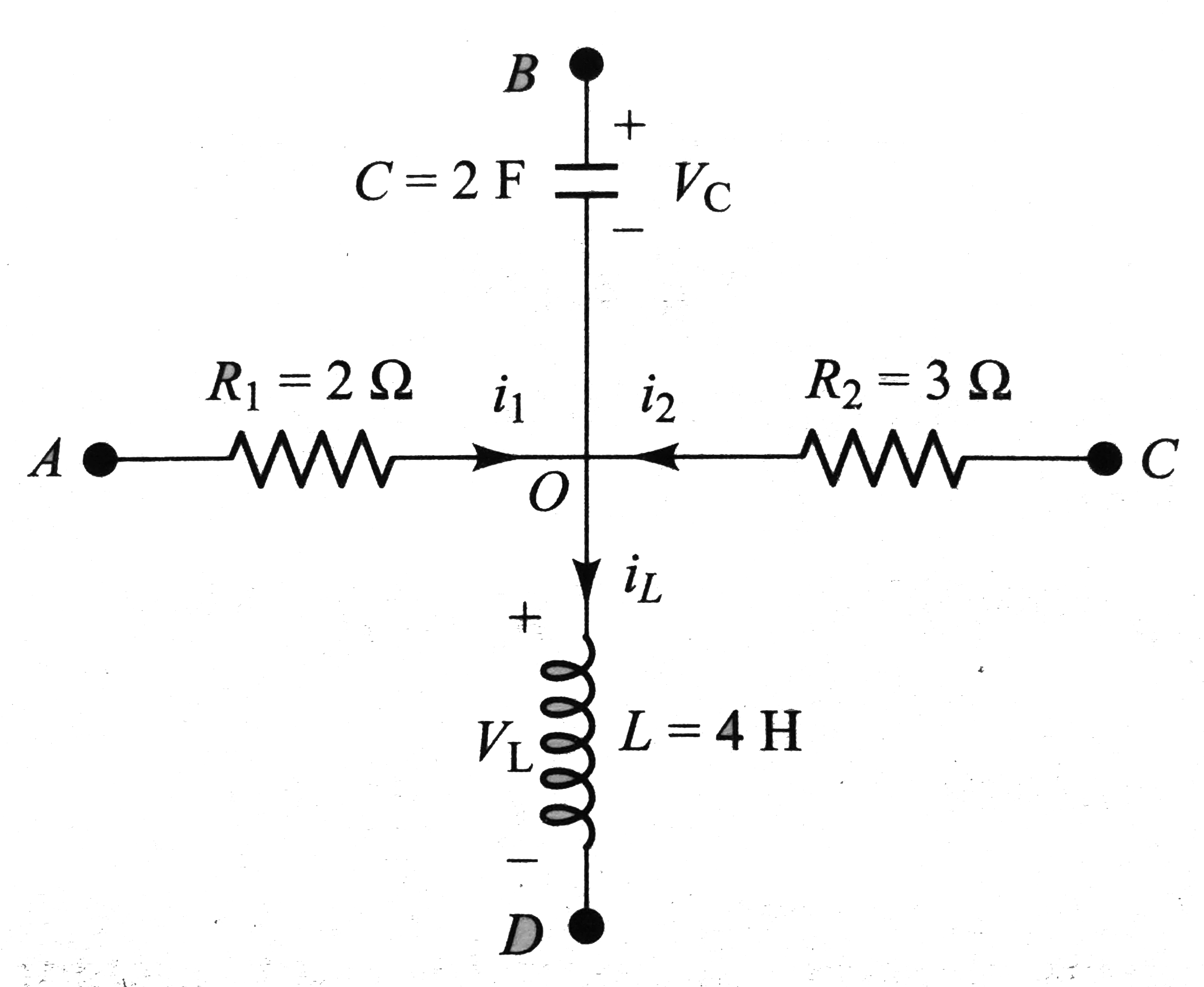
In the Figure shown i1=10e−2tA,i2=4A and VC=3e−2tV. Determine
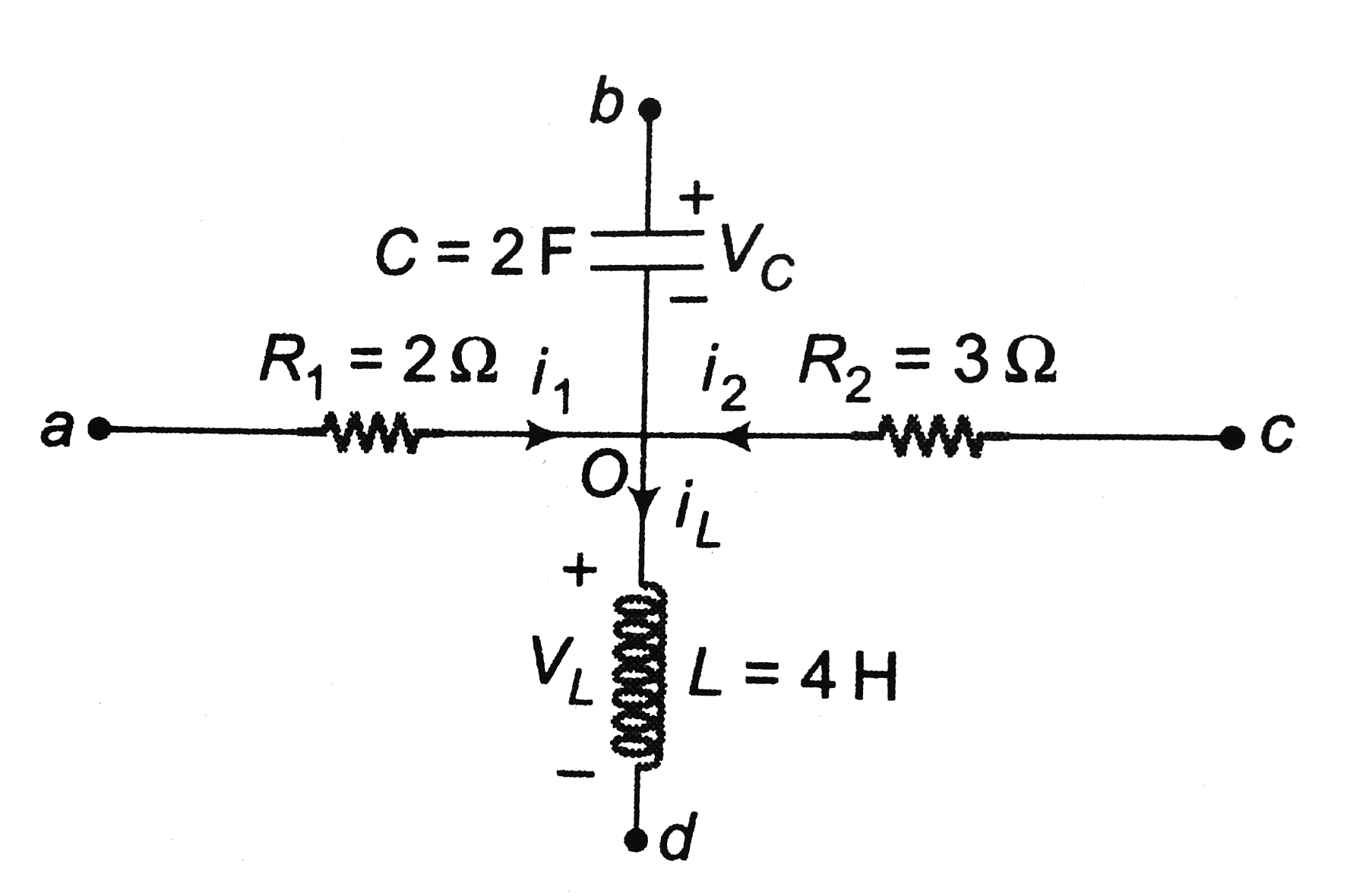
a. iL and VL b. Vac,Vab,Vcd
A
8e−2tV
B
12e−3tV
C
17e−2tV
D
16e−2tV
Video Solution
Text Solution
The correct Answer is:C
Instanctaneous current in the capacitor,
q=CVC=(2)(3e−2t)=6e−2tA
Current, iC=dqdt=−12e−2tA
This current flows from B to O.
From KVL, we have
iL=i1+i2+iC=10e−2t+4−12e−2t
=(4−2t−2t)A=[2+2(1−e−2t)]A
iLvs. time graph is as shows in Fig lt
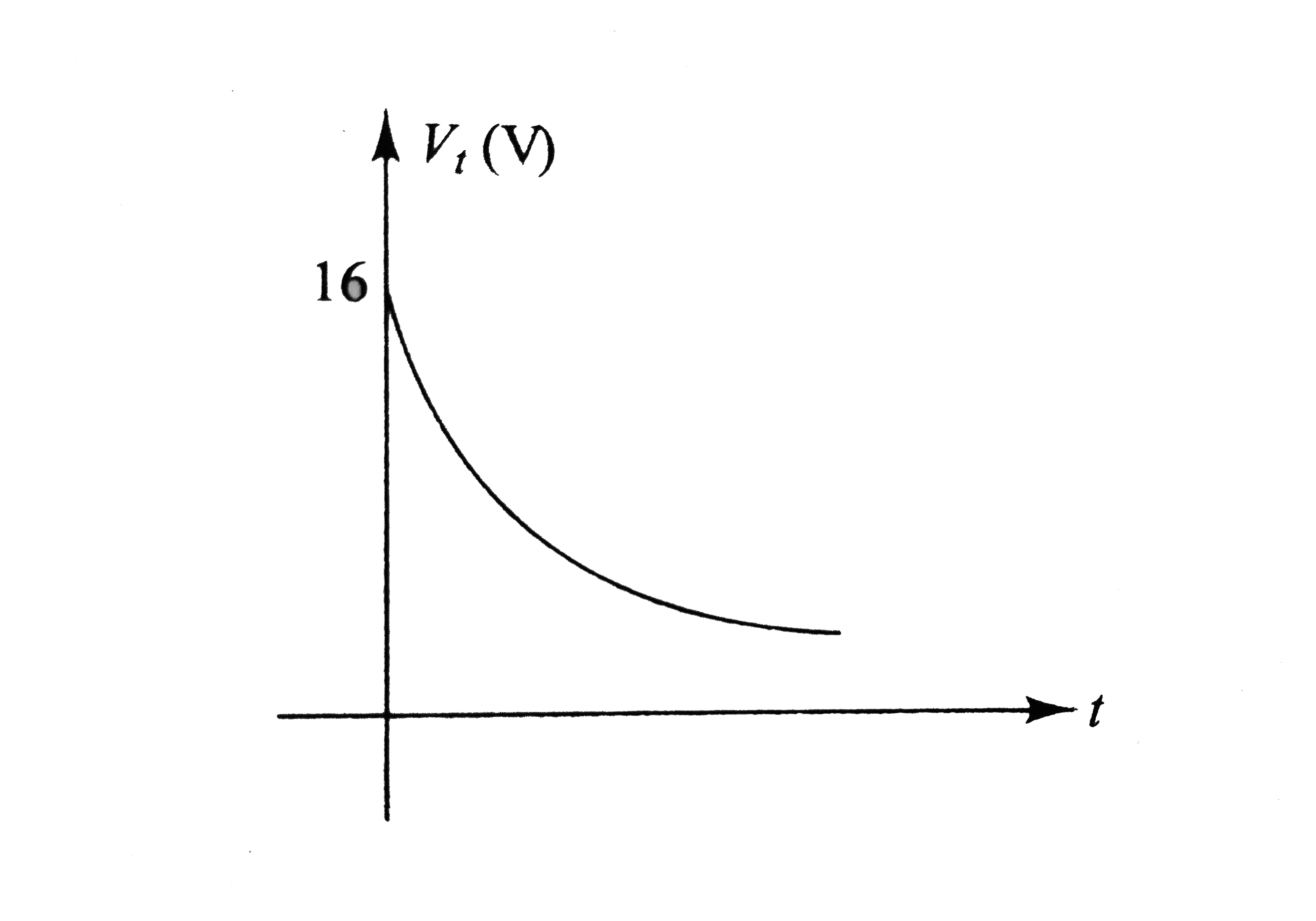
iL increases from 2A to 4A expontially.

VL=LdiLdt
=(4)ddt(4−2e−2t)=16e−2tV
VL decreases exponentially from 16A to 0 as shows in Fig
To determine VAC, we begin from A and at C. From KVL,
we have

VA−i1R1+i2R2=VC
VA−VC=i1R1−i2R2
Substituting the values, we have
VAC=(10e−2t)(2)−(4)(3)
VAC=(20e−2t−12)V
At t=0, VAC=8V
At t=∞, VAC=−12V
Therefore, VAC decrease exponentially from 8V to 12V.
Similarly, we have from A to B
VA−i1R1+VC=VB
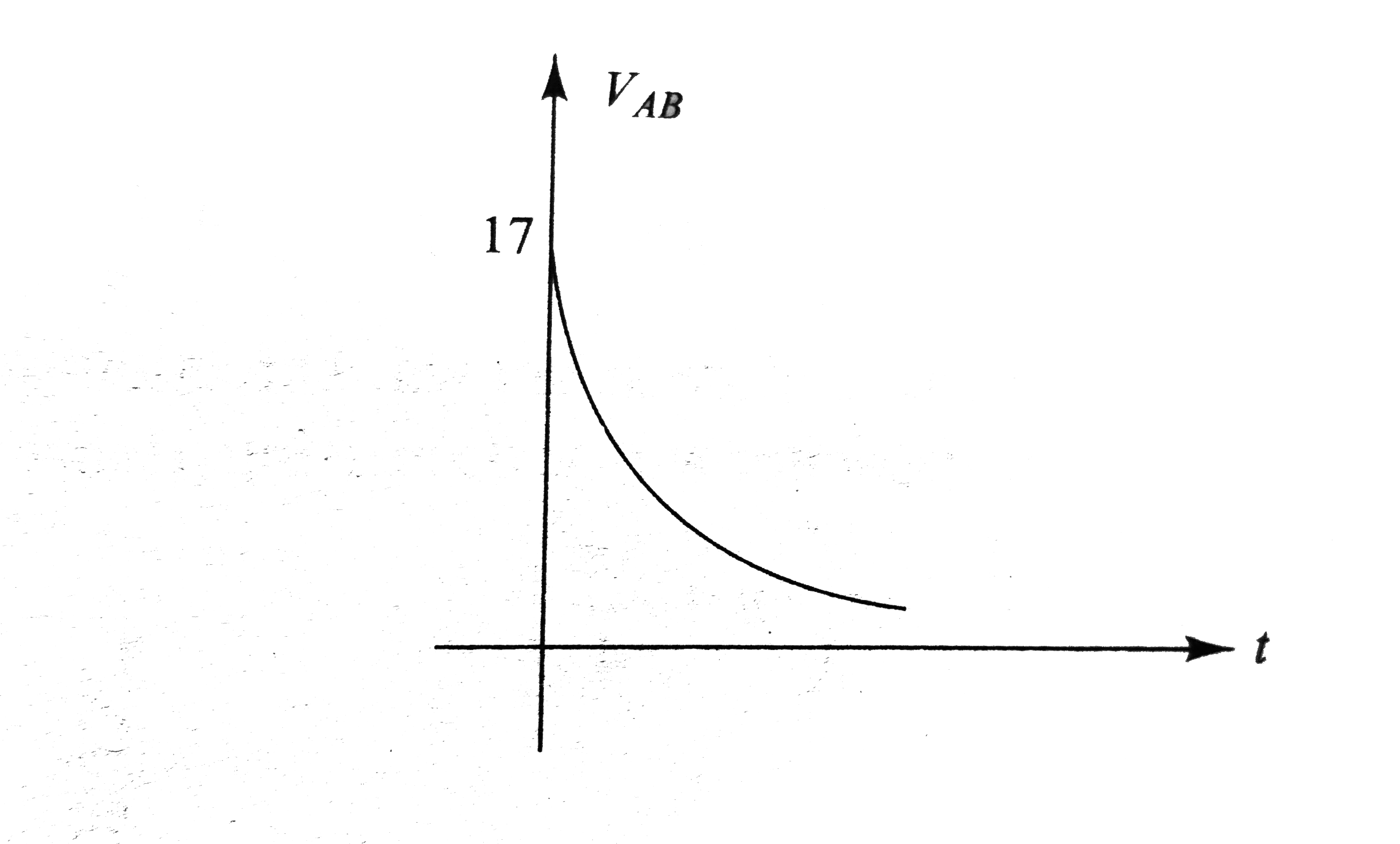
VAB=VA−VB=i1R1−VC 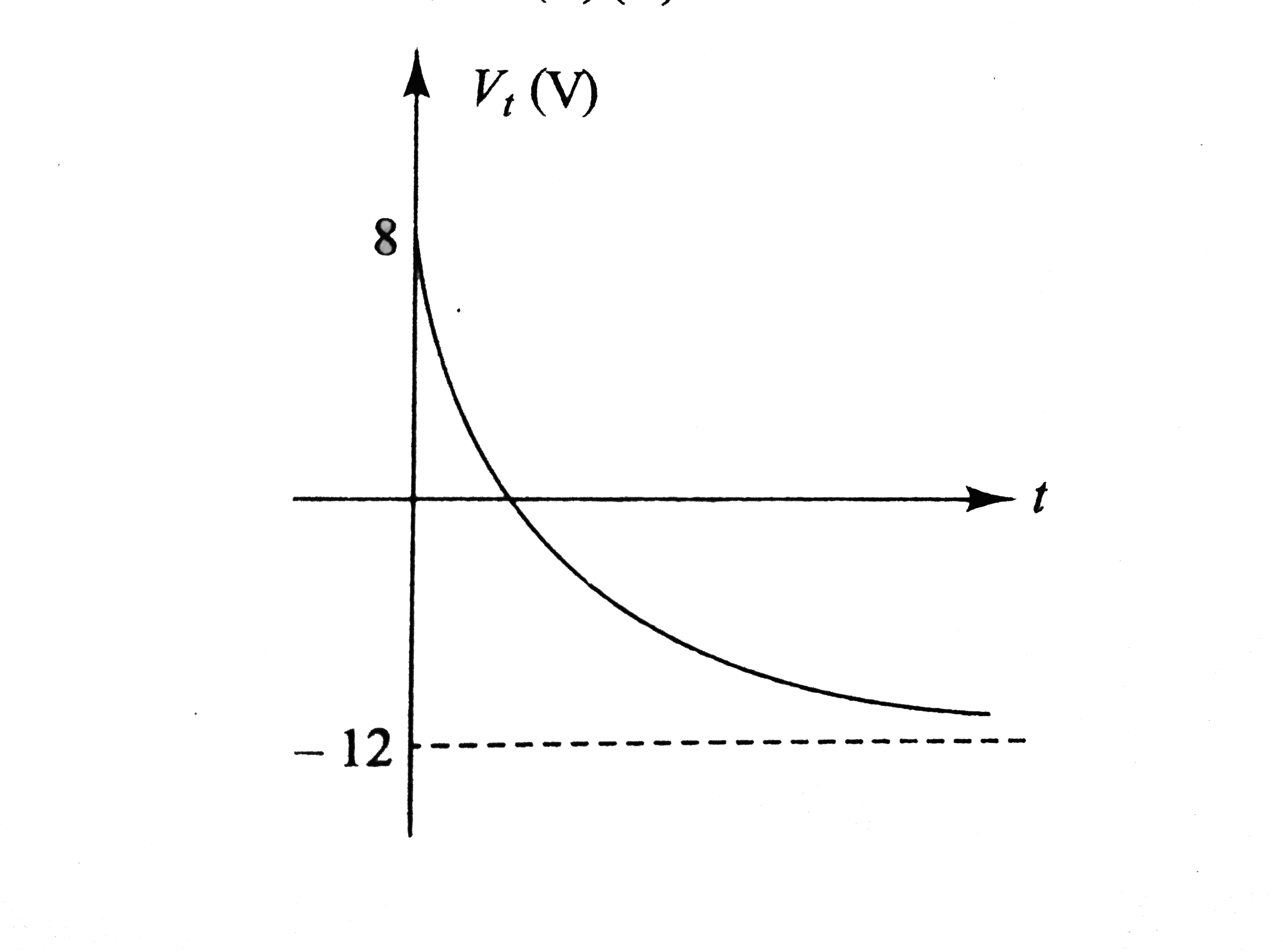
Substituting the values, we have
VAB=(10e−2t)(2)−3e−2t
VAB=17e−2tV
Thus, VAB decreases exponentially from 17V to 0.
As we move from C to D,
VC−i2R2−VL=VD
VCD=VC−VD=i2R2+VL
Substituting the values we have,
VCD=(4)(3)+16e−2t
VAD=(12+16e−2t)V
At t=0,VCD=28V
and at t=∞,VCD=12V
i.e., VCD decreases exponentially from 28V to 12V.
|
Topper's Solved these Questions
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Exercises (integer)
8 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Archives (fills In The Blanks)
3 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Exercises (assertion-reasoning)
2 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICSCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
28 Videos
- KINETIC THEORYBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORYEXERCISE - Question Bank
31 Videos
Similar Questions
Knowledge Check
In figure i1=10e−2tA,i2=4A,vC=3e−2tV
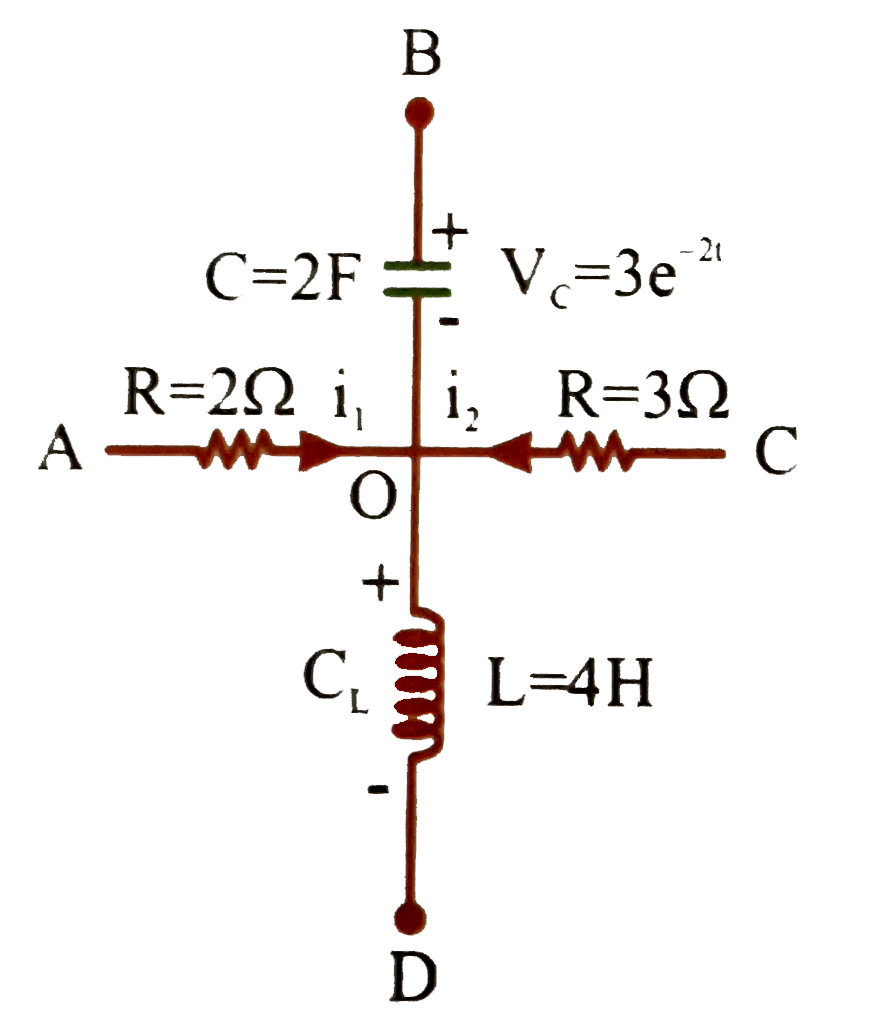
The current iL isA[2−2(1−e−2t)]AB[2+2(1−e−2t)]AC[3−2(1−e−2t)]AD[2+3(1−e−2t)]AIn figure i1=10e−2tA,i2=4A,vC=3e−2tV
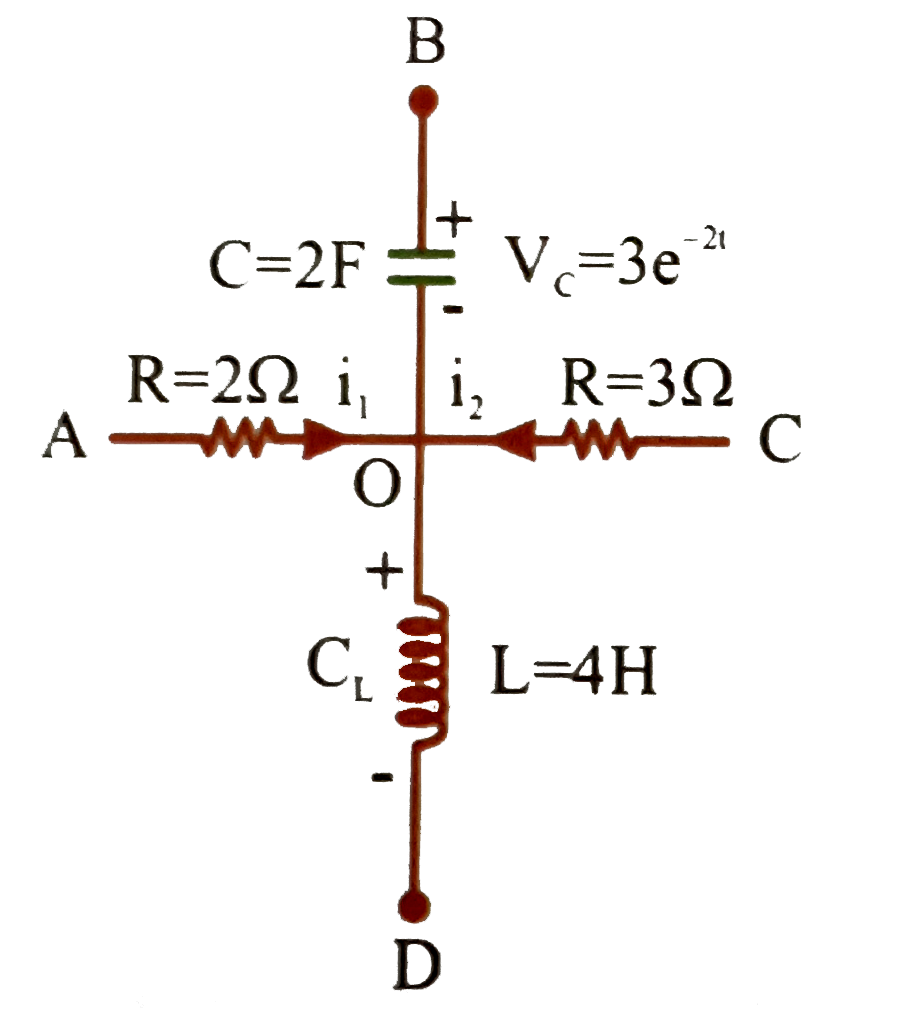
The potential difference across inductor VL is :A8e−2tVB9e−2tVC16e−2tVD18e−2tVIn Fig i1=10e−2tA, i2=4A, and VC=3e−2tV.
the vartiation of potential difference across A and C(VAC) with time can be respresented asA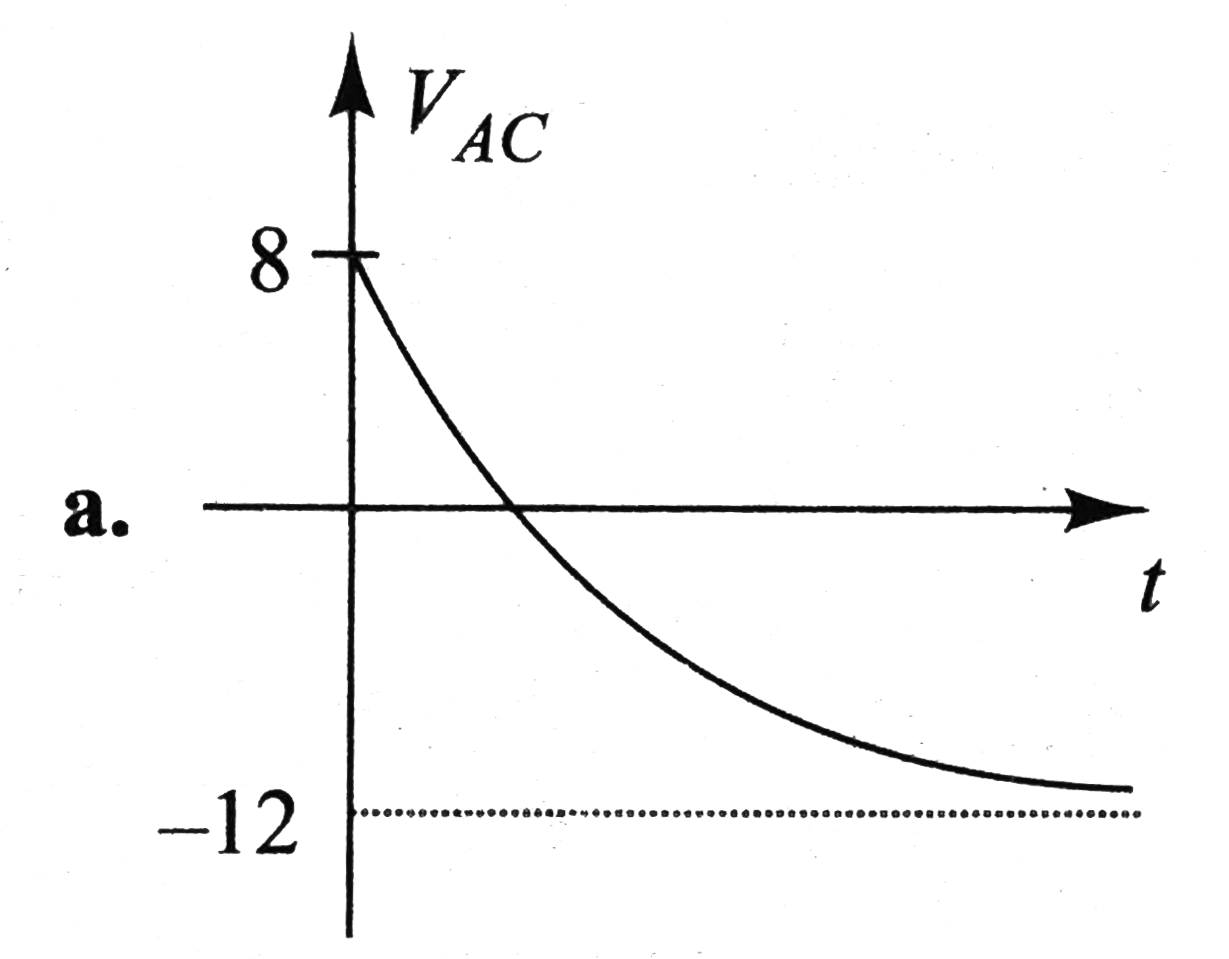 B
B C
C D
D
In the figure shown i=10e−41A. Find BLandVab

View SolutionIn Fig i1=10e−2tA, i2=4A, and VC=3e−2tV.
The variation of potential difference across C and D(VCD) with time can be expressed as
View SolutionIn figure i1=10e−2tA,i2=4A,vC=3e−2tV
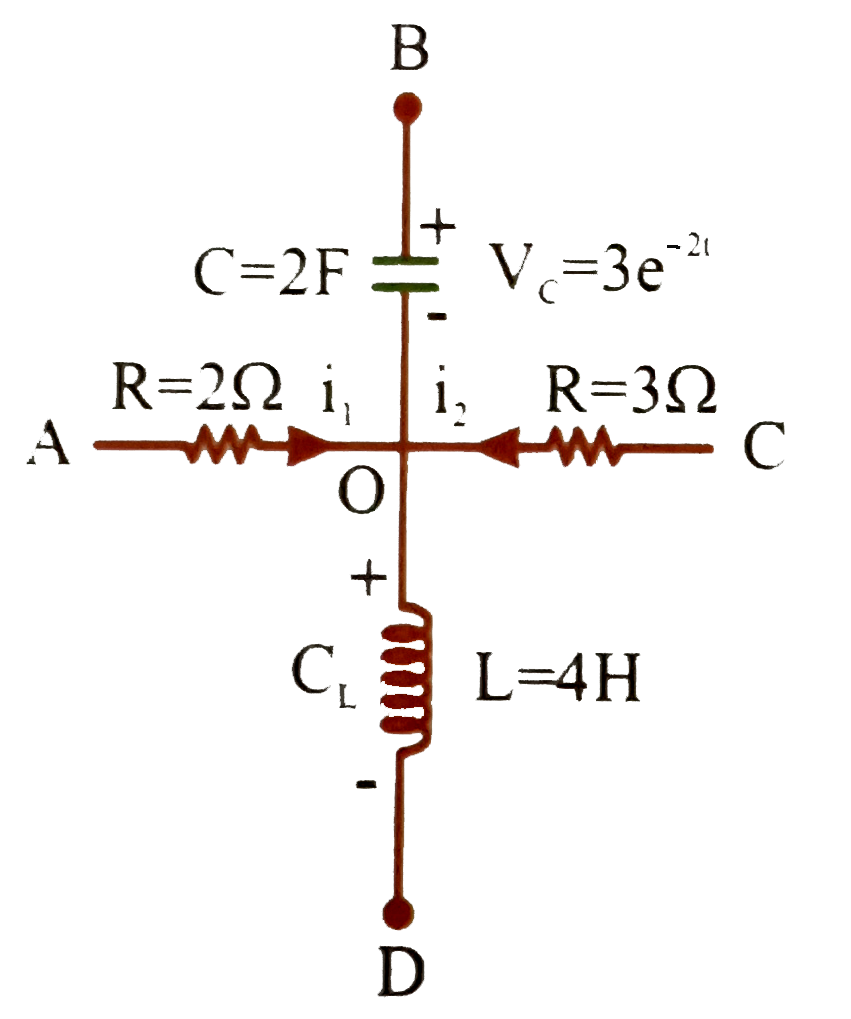
The potential difference across AB(VAB) is:
View SolutionIn Fig i1=10e−2tA, i2=4A, and VC=3e−2tV.
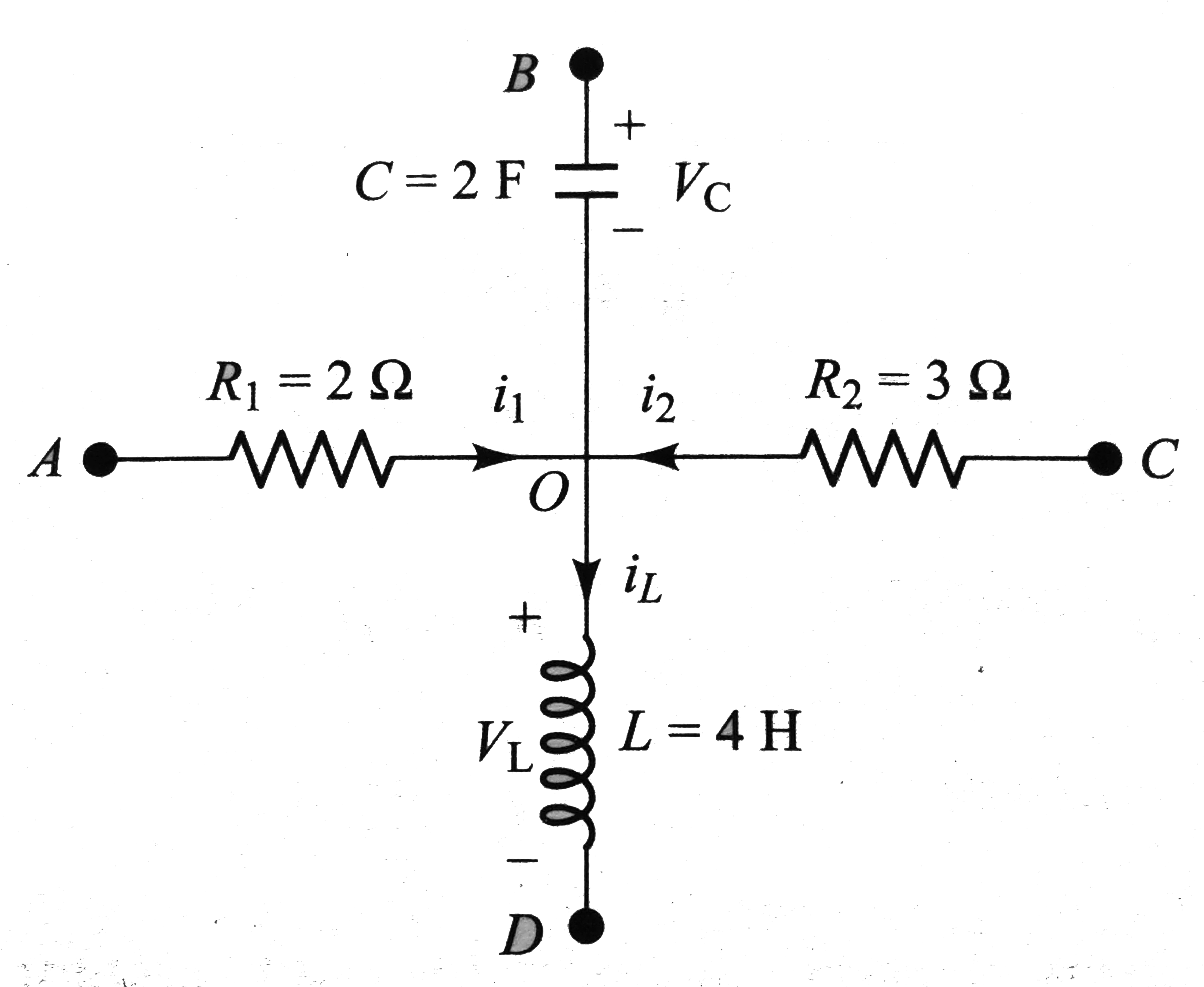
The variation of current in the inductor with time can be represented as
View SolutionIn figure i1=10e−2tA,i2=4A,vC=3e−2tV
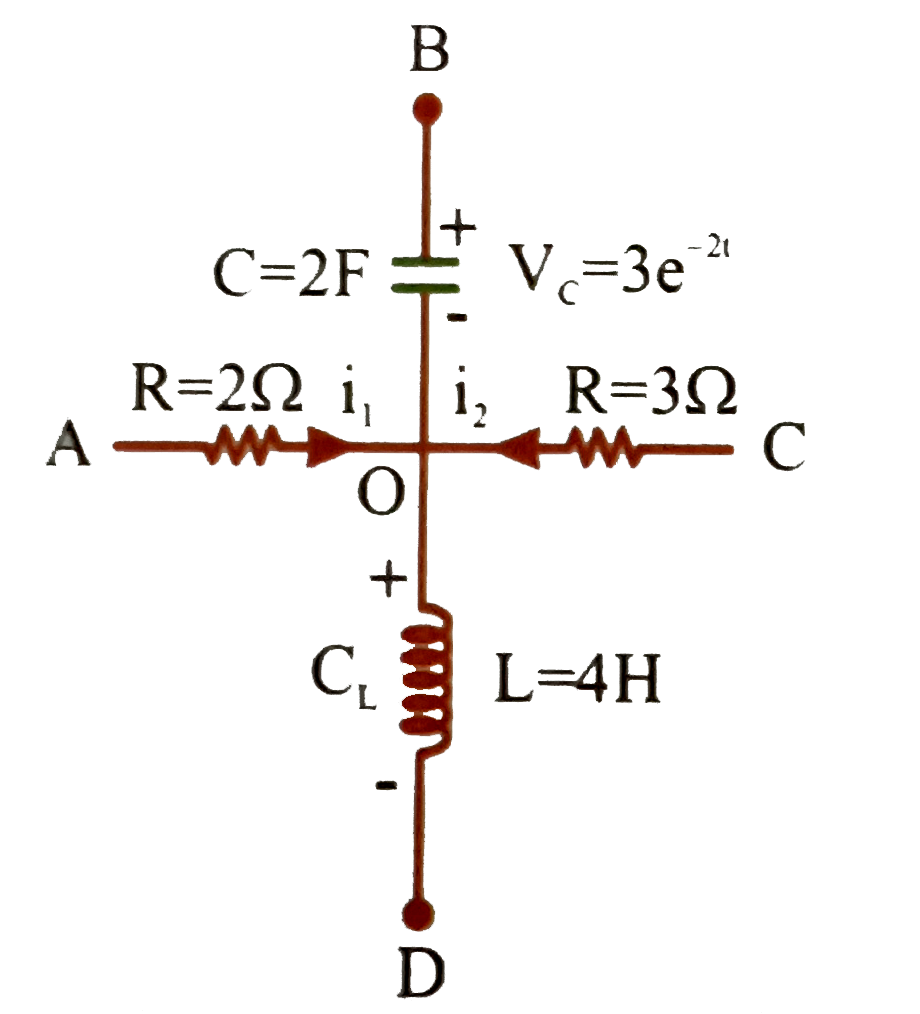
The variaton of current in the inductor with time can be repesented as :
View Solution


