In the figure shown initial spring is in unstretched state and blocks are at rest. Now 100N force is applied on block AandB as shown in figure. After same time velocity of 'a' becomes 2m/s and that of 'B' 4m/s and block A displaced by amount 10cm and spring is spring is streched by amount 30cm. Then work done by spring force on A will be:

9/3J
−6J
6J
None of these
The correct Answer is:B
Wspring+W100N=Δk(onA)
Wspring+(100)(10100)=12(2)(2)2
Wspring=4−10=−6J
Topper's Solved these Questions
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Assertion Reasoning
17 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - NEET Questions
49 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Collision
31 Videos
- WAVES AND ACOUSTICSBOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Chapter Test
30 Videos
Similar Questions
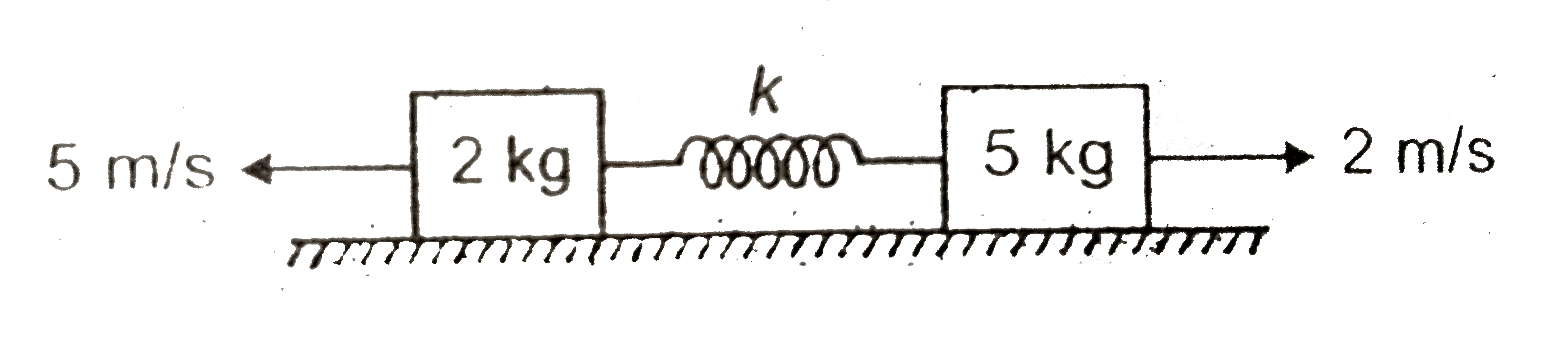
Two blocks of mass 2kg and 5kg are given speed as shown in the figure. System is lying on a frictionless surface and the blocks are connected by a massless spring if spring constant 35Nm. Find the maximum compression in the spring.
View SolutionInitially block shown is at rest and the spring is unstretched, when a constant force F begins to act on it neglect friction. Find
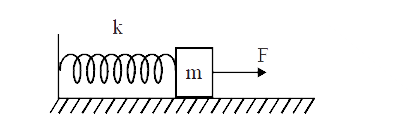
maximum extension in the spring
View Solution
Knowledge Check
A constant force F is applied on a spring block system as shown in figure. The mass of the block is m and spring constant is k. The block is placed over a smooth surface. Initially the spring was unstretched. Choose the correct alternative(s)
 AThe block will executes SHMBAmplitude of oscillation is F2KCTime period of oscillation is 2π√mkDThe maximum speed of block is √2Fx−kx2m (Here, x=F/k).
AThe block will executes SHMBAmplitude of oscillation is F2KCTime period of oscillation is 2π√mkDThe maximum speed of block is √2Fx−kx2m (Here, x=F/k).A block of mass m is suspended by different springs of force constant shown in figure.
 AT1=T2=T4BT1=T2andT3=T4CT1=T2=T3DT1=T3 and T2=T4
AT1=T2=T4BT1=T2andT3=T4CT1=T2=T3DT1=T3 and T2=T4A constant force produces maximum velocity V on the block connected to the spring of force constant K as shown in the figure. When the force constant of spring becomes 4K, the maximum velocity of the block is
 AV/4B2VCV/2DV
AV/4B2VCV/2DV
In the situations shown in the figure surfaces are frictionless. Find the maximum extension of the springs if blocks are initially at rest and springs are initially in natural lengths.

View SolutionEach of the blocks shown in figure has mass 1 kg. The rear block moves with a speed of 2 m/s towards the front block kept at rest. The spring attached to the front block islight and has a spring constant 50 N/m. find the maximum compression of the spring.

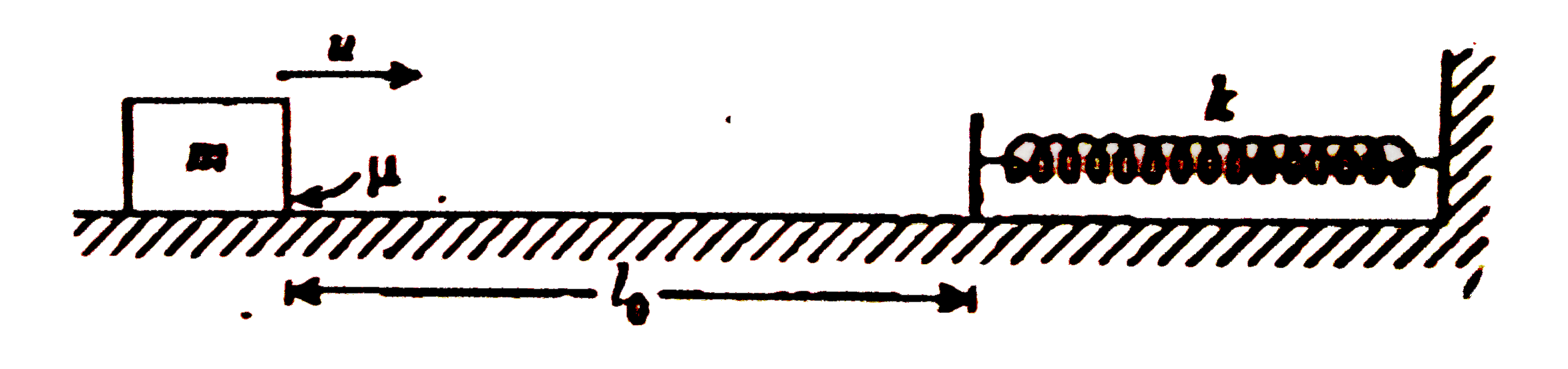
View SolutionFigure. shows a rough horizontal plane which ends in a vertical wall, to which a spring is connected, having a force constant k. Initially spring is in its relaxed state. A block of mass m starts with an initial velocity u towards the spring from a distance l0 from the end of spring shown. When block strikes at the end ofthe spring, it compresses the spring and comes to rest. Find the maximum compression in the spring. The friction coefficient between the block and the floor is μ..
View SolutionIn the figure shown, the system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10 N/m.
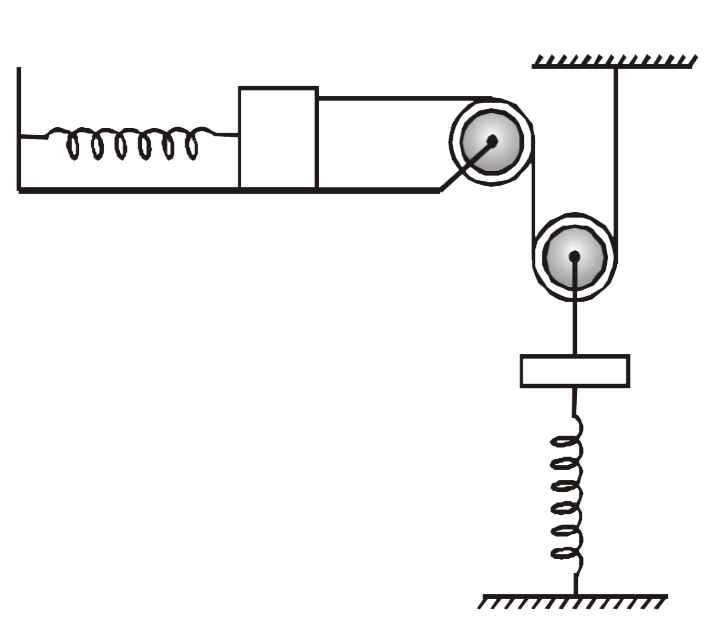
Maximum speed of the block placed horizontally is:
View SolutionIn the figure shown a block of masss m is atteched at ends of two spring The other ends of the spring are fixed The mass m is released in the vertical plane when the spring are released The velocity of the block is maximum when
View Solution
