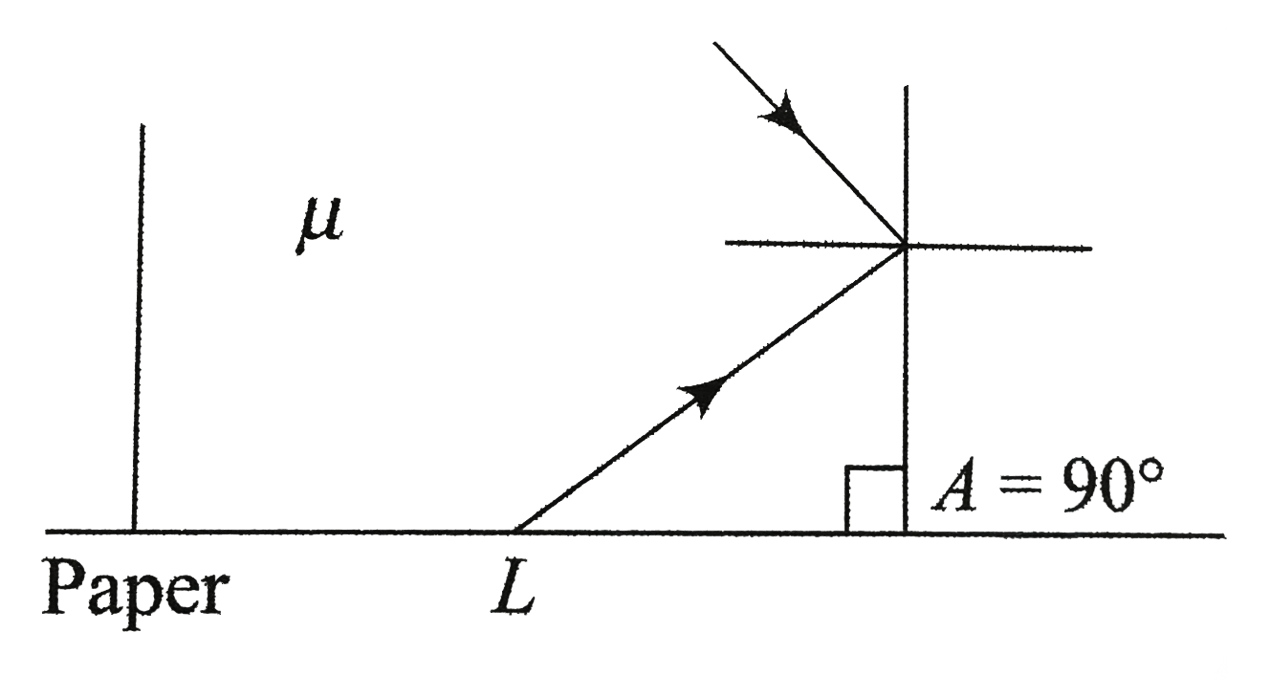
In the figure shown, μ1>μ2. Find minimum value of i so that TIR never takes place at P.

The correct Answer is:β=θC.
Let us take β=θC.Then,α=90∘−βorα=90∘−θC
Here, sinθC=μRμD=μ2μ1
∴θC=sin−1(μ2μ1)
Applying Snell's law at point Q,
μ2sini=μ1sinα=μ1sin(90∘−θC)
=μ1cosθC=μ1cossin−1(μ2μ1)
∴i=sin−1[(μ1μ2)cossin−1(μ2μ1)]
Now, we can see that starting from this value of i, we get β=θC.
If i is increased from this value, then α will also increase(becomes>90∘−θC) and β decreases from θC(becomes<θC) and no TIR takes place at P.
So far no TIR condition i has to be increased from the above value. Or this is the minimum value of i.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Example Type 101videos
REFRACTION OF LIGHT
- BOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Example Type 113videos
REFRACTION OF LIGHT
- BOOK - DC PANDEYCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective9videos
REFLECTION OF LIGHT
- BOOK - DC PANDEYCHAPTER - SEMICONDUCTORSEXERCISE - Subjective12videos
SEMICONDUCTORS
Similar Questions
Knowledge Check
- Question 1 - Select One
A hollow sphere of mass 2kg is kept on a rough horizontal surface. A force of 10N is applied at the centre of the sphere as shown in the figure. Find the minimum value of μ so that the sphere starts pure rolling. (take g=10ms−2)
 A√3×0.16B√3×0.08C√3×0.1Ddata insufficient
A√3×0.16B√3×0.08C√3×0.1Ddata insufficient - Question 2 - Select One
In the figure shown, μ1>μ2>μ3. What are the limits of angle i so that it is neither get total internal reflection at AB nor at CD ?
 Asini<μ2(μ2)Bsini<μ3(μ1)Csini<μ3(μ2)DNone of these
Asini<μ2(μ2)Bsini<μ3(μ1)Csini<μ3(μ2)DNone of these
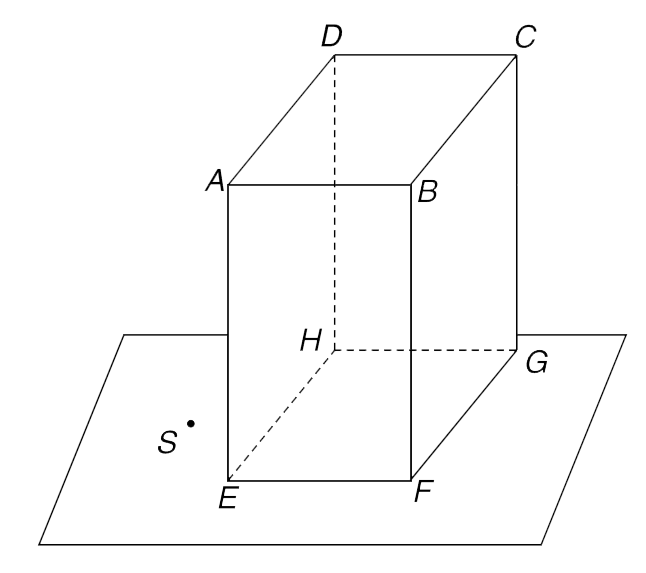
A large rectangular glass block of refractive index μ is lying on a horizontal surface as shown in Figure. Find the minimum value of μ so that the spot S on the surface cannot be seen through top plane ‘ABCD’ of the block.
 View Solution
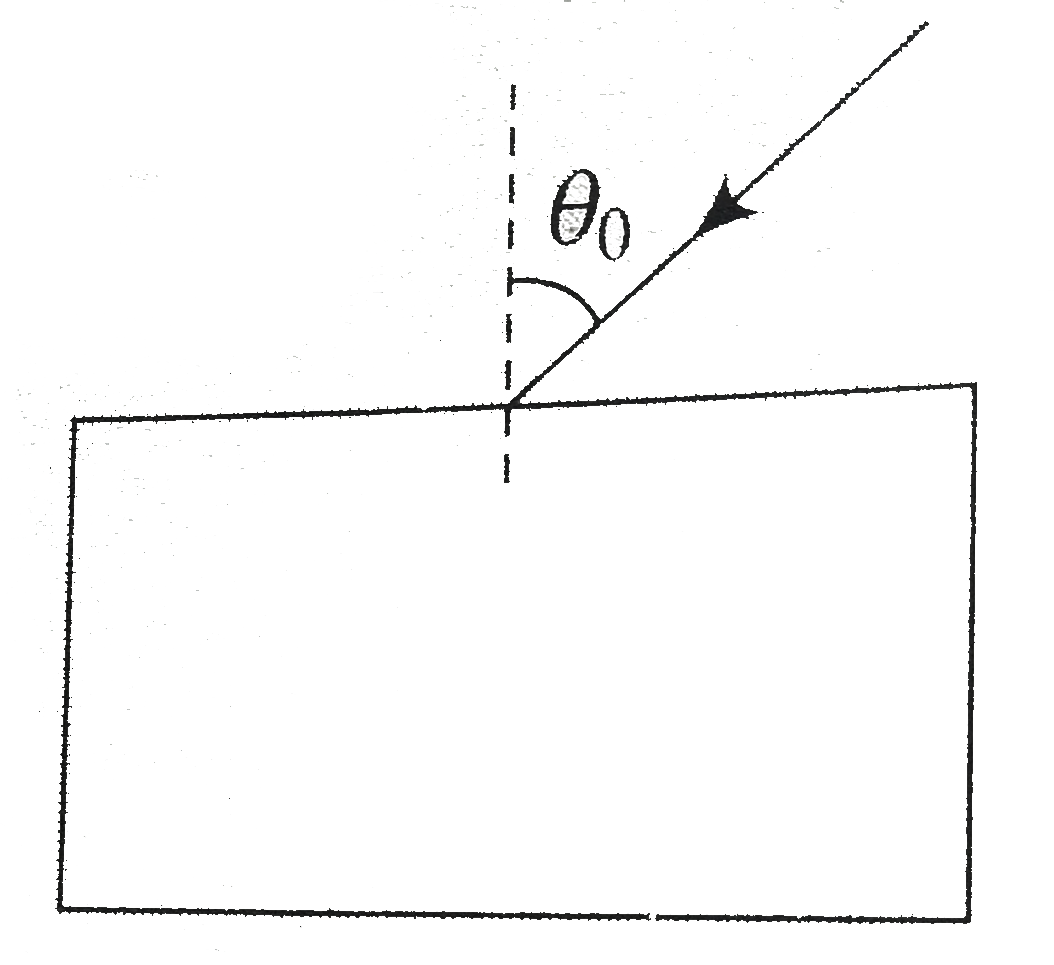
View SolutionA slab of refractive index μ is placed in air and light is incident at maximum angle θ0 from vertical. Find minimum value of μ for which total internal reflection takes place at the vertical surface.
 View Solution
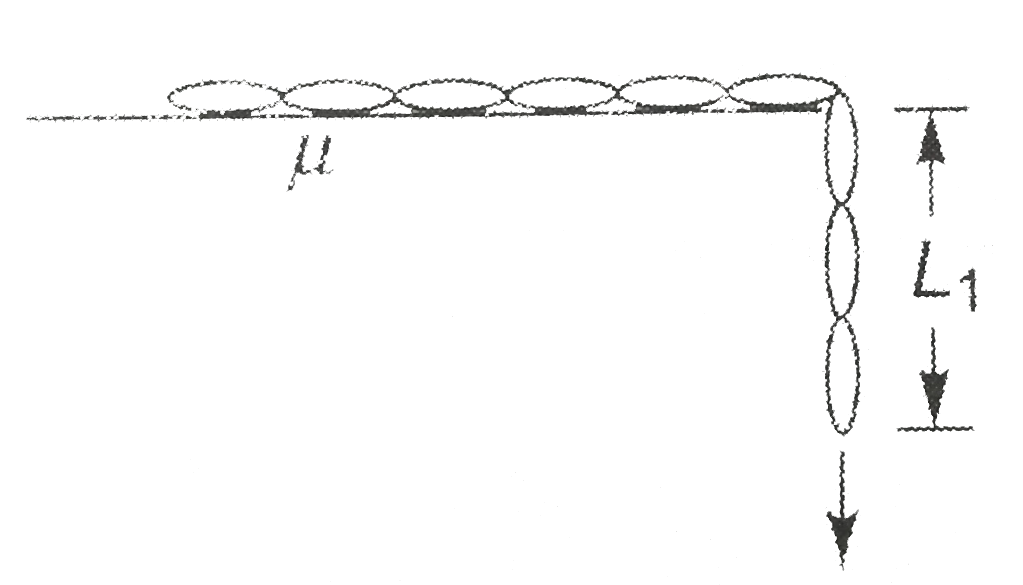
View SolutionA homogeneous chain of length L lie on a table. If the coefficent of friction is μ , find the maximum length L1 of the chain which can hang from the edge of the table without the chain sliding down.
(b) Consider the situation as shown in the figure. Find teh minimum value of m so that the blocks do not move.
 View Solution
View SolutionA small block of mass m is projected on a larger block of mass 10m and length l with a velocity v as shown in the figure. The coefficient of friction between the two block is μ2 while that between the lower block and the ground is μ1. Given that μ2>11μ1.

(a) Find the minimum value of v, such that the mass m falls off the block of mass 10m .
(b) If v has minimum value, find the time taken by block m to do so.View SolutionConsider the situation as shown in the figure. Find the maximum value of m1/m2 so that the system remains at rest. What will happen if tanθ<μ?
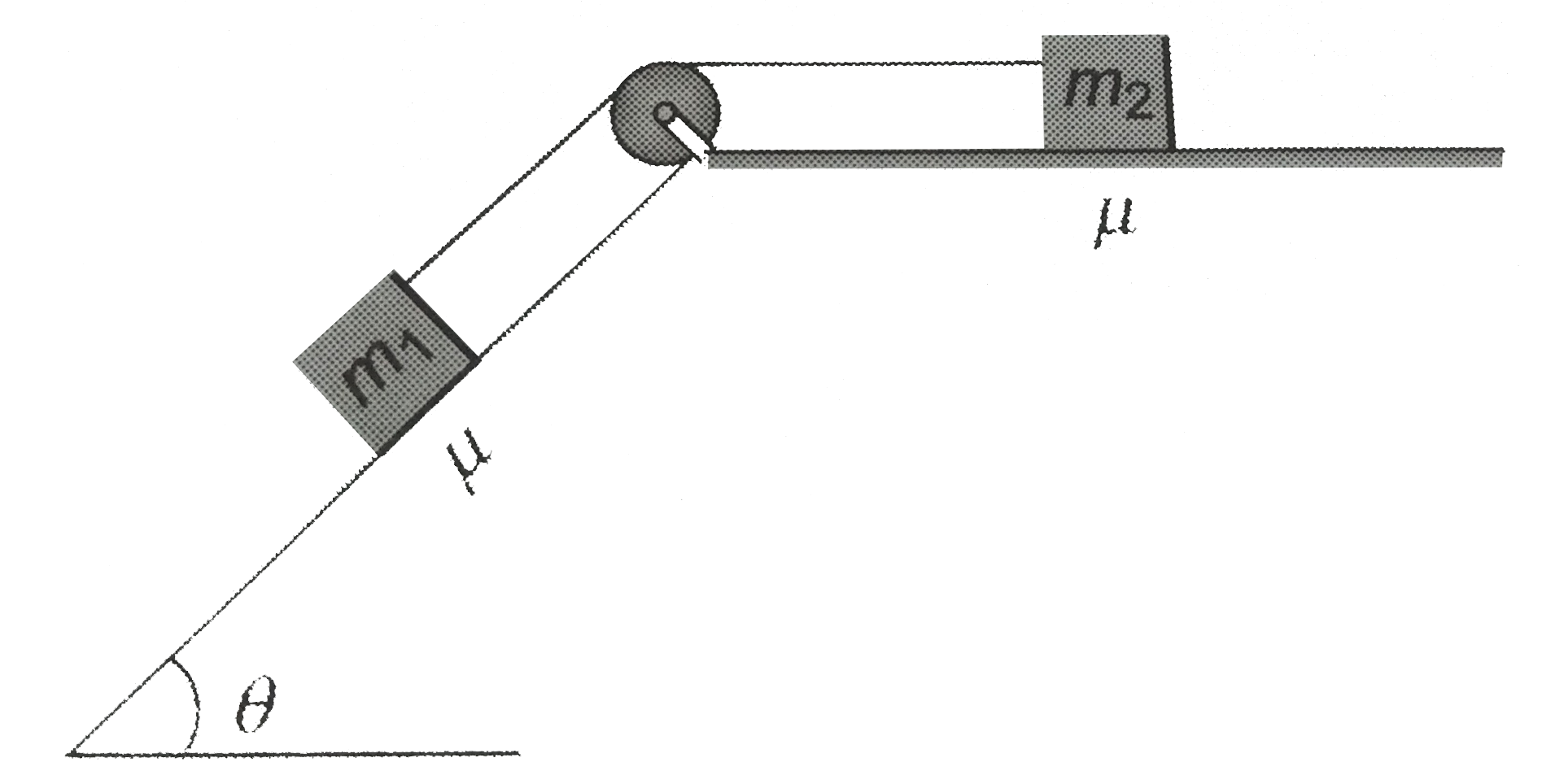 View Solution
View SolutionA glass rod having square cross-section is bent into the shape as shown in the figure. The radius of the inner semi-circle is R and width of the rod is d. Find the minimum value of d/R so that the light that enters at A will emerge at B. Refractive index of glass is μ=1.5
 View Solution
View Solution